4. Перспектива точки, расположенной на предметной плоскости τ.

На рис. 1.5, а точка A находится на предметной плоскости Τ. В этом случае вторичная проекция A_T совпадает с самой точкой A. Как видно из приведённых построений, перспектива A_K точки A всегда совпадает с

п ерспективой A_KB вторичной проекции этой точки. На картинной плоскости Π_K (рис. 1.5, б) перспективы A_K и A_KB всегда расположены ниже линии горизонта hh. Однако, если точка A находится бесконечно далеко от картинной плоскости Π_K, то A_K и A_KB будут находиться на линии горизонта hh.

5. Перспективы точек, расположенных на одном перпендикуляре к предметной плоскости Τ. 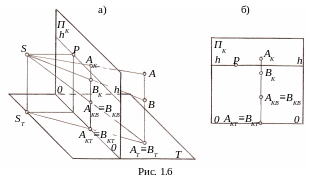Пусть точки A и В расположены на одном перпендикуляре к предметной плоскости Τ (рис. 1.6, а). Выполненные построения показывают, что перспективы A_K и В_K точек A и В и перспективы A_KB и В_KB вторичных проекций точек A_T и В_T (рис. 1.6, б) расположены на одном перпендикуляре к основанию картины OO. При этом песпективы A_KB и В_KB вторичных проекций A_T и В_T совпадают.

1.2. Перспектива прямой линии

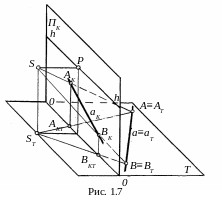Известно, что положение прямой линии в пространстве вполне определяют две её точки. На прямой а, расположенной в плоскости Τ (рис. 1.7), возьмём две некоторые точки A и В. Вторичные проекции A_T и В_T этих точек будут совпадать с ними. Перспективы A_K и В_K точек A и В на картинной плоскости Π_K расположены в точках пересечения перпендикуляров, проведённых к основанию картины OO из точек A_KT и В_KT, с лучами SA и SB. Лучевая плоскость, образованная лучами SA и SB пересекается с картинной плоскостью Π_K по прямой линии. Поэтому перспектива прямой линии есть прямая линия.

Прямые линии в предметном пространстве по отношению к картинной и предметной плоскостям могут располагаться различным образом и подразделяются на прямые общего и частного положения.

1. Прямые общего положения. Прямые, расположенные под острыми углами к картинной и предметной плоскости, называются прямыми общего положения. Для построения перспективы прямой общего положения достаточно задаться двумя её любыми точками, найти их перспективы, соединив их прямой линией и продолжив эту линию в обе стороны.

Однако перспективу прямой линии желательно строить не по случайным точкам на ней, а по так называемым особым точкам. К особым точкам прямой линии относят начальную точку A_H прямой (рис. 1.8), которая является точкой пересечения прямой a с картинной плоскостью Π_K, и бесконечно удалённая точка F^∞ на прямой a.

Р ис. 1.8

При заданных прямой a и её вторичной проекции a_T начальную точку A_H можно найти на пересечении перпендикуляра, проведённого из точки A_O, являющейся точкой пересечения a_T с основанием картины OO, с продолжением прямой линии a. При этом, так как точка A_HΠ_K, то она одновременно является перспективой этой точки.

Перспектива бесконечно удалённой точки F^∞ на прямой линии a называется перспективой предельной точки прямой или точкой схода перспективы прямой. Перспектива A_K некоторой точки A на прямой линии a, как было рассмотрено ранее, находится на пересечении луча зрения, исходящего из точки S к точке A. Легко убедиться, что по мере удаления точек на прямой линии a от точки A, лучи зрения к ним располагаются всё ближе к своему крайнему положению, параллельному прямой линии a. Таким образом, проведя из точки S луч зрения параллельно прямой a до пересечения с картинной плоскостью Π_K, находим точку схода F₁ перспективы этой прямой. Для этого из точки S_T проводим прямую линию параллельно a_T до пересечения с основанием OO картины в точке F_T. Точка F₁ схода при этом будет находиться на пересечении перпендикуляра к основанию OO картины, восстановленном в точке F_T, и луча зрения, проведённого параллельно прямой a. Перспективу a_K бесконечной прямой линии a можно построить, соединив отрезком прямой линии найденные перспективы A_H и F₁.

Изображение на картинной плоскости только перспективы прямой линии не определяет её положения в пространстве. Перспективное изображение прямой обратимо, если оно дополнено перспективой вторичной проекции этой прямой.

Если из точки S проведём луч параллельно вторичной проекции a_T, то на пересечении его с картинной плоскостью Π_K найдём точку F₂ схода перспективы бесконечно удалённой точки вторичной проекции a_T прямой a. Перспективу a_KВ вторичной проекции a_T можно построить, если соединить отрезком прямой линии начальную точку A_O и точку схода F₂.

Заметим, что для прямых общего положения точки схода F₁ и F₂ перспектив этих прямых и их вторичных проекций всегда лежат на одном перпендикуляре к линии горизонта hh.

2. Прямые частного положения. Прямые, параллельные или перпендикулярные предметной или картинной плоскости, либо расположенные в этих плоскостях, называются прямыми частного положения. Рассмотрим последовательность построения перспектив для каждого вида прямых.

2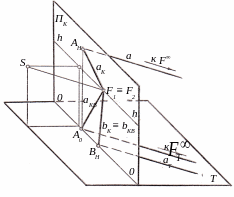 .1. Прямые, параллельные предметной плоскости Τ. На рис. 1.9 задана прямая a||Τ и её вторичная проекция a_T. При построении перспектив этих прямых воспользуемся изложенным выше способом нахождения

b≡b_T

Рис. 1.9

начальных A_H и A_O и перспектив бесконечно удалённых F^∞ и точек на них. Как видно из выполненных построений начальные точки A_H и A_O прямой a и её вторичной проекции a_T расположены на одном перпендикуляре к основанию OO картины. При этом точка A_O находится в точке пересечения продолжения вторичной проекции a_T с картинной плоскостью Π_K на основании OO. Точка A_H находится в точке пересечения продолжения прямой a с перпендикуляром, восстановленном к основанию OO в точке A_O.

Точка схода F₁ перспективы бесконечно удалённой точки F^∞ прямой a расположена в точке пересечения луча, проведённого из точки S параллельно прямой a, с линией горизонта hh. Точка схода F₂ перспективы бесконечно удалённой точки прямой a_T будет совпадать с точкой F₁, так как луч, проведённый из точки S параллельно прямой a_T, будет тем же самым лучом, поскольку a||a_T.

Соединяя отрезками прямых соответствующие начальные точки и точки схода перспектив этих прямых, получаем искомые перспективы a_K и a_KВ заданной прямой a и её вторичной проекции a_T. Легко убедиться, что точка схода перспективы прямой b(bΤ и b||a) также совпадает с точкой схода F₁.

Таким образом, точка схода перспектив прямых, параллельных предметной плоскости Τ и расположенных в ней, всегда находится на линии горизонта hh.

Среди рассматриваемых прямых имеются такие, которые наклонены под углом 45° к картинной плоскости Π_K. На рис. 1.10 прямая a лежит в

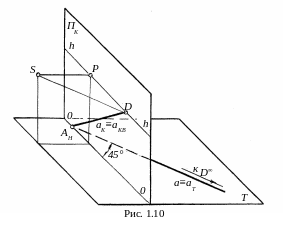
плоскости Τ и наклонена к Π_K под углом 45°. Построим перспективу прямой a по начальной точке A_H, которая находится на пересечении продолжения прямой с основанием OO картины, и точке D схода её перспективы.

Для нахождения точки D схода бесконечно удалённой точки D^∞ прямой a из точки S проводим луч параллельно прямой до пересечения с картинной плоскостью Π_K на линии горизонта hh в точке D. Треугольник SPD прямоугольный и равнобедренный. Поэтому SP=PD. Для прямых, наклонённых к основанию OO картины под углом 45° с другой стороны будем иметь точку схода их перспектив по другую сторону от центра P картины на том же расстоянии.

Точка схода D называется дистанционной точкой и является одним из важнейших элементов при построении перспективных изображений геометрических объектов.

2.2. Прямые, параллельные картинной плоскости Π_K. Прямые, параллельные картинной плоскости Π_K или расположенные в ней, а так же их вторичные проекции, не имеют точек схода перспектив этих прямых из-за отсутствия предельных точек на них. Отсутствуют и начальные точки, т.е. точки пересечения прямых с Π_K.

Поэтому построение перспектив прямой a, параллельной картинной плоскости Π_K, и вторичной проекции a_T можно выполнить, например, по двум случайным точкам A и В и их вторичным проекциям A_T и В_T рис. 1.11. Порядок построения перспектив таких точек рассмотрен в п.1 раздела 1.1. Из рис. 1.11 видно, что перспективы прямых, параллельных картинной плоскости, параллельны этим прямым, а перспективы вторичных проекций прямых параллельны основанию OO картины.

Рис.1.11

Естественно, что перспектива b_K прямой b, расположенной в картинной плоскости Π_K, и перспектива b_KВ вторичной проекции b_T попарно совпадают.

2.3. Прямые, перпендикулярные картинной плоскости Π_K. На рис. 1.12 задана прямая a, расположенная в предметном пространстве перпендикулярно картинной плоскости Π_K, и её вторичная проекция a_T.

Начальные точки A_H и A_O прямых a и a_T находятся на одном перпендикуляре к основанию OO картины. Для нахождения точки схода перспективы бесконечно удалённой точки прямой a из точки S проводим луч параллельно прямой a, который пересечёт Π_K на линии горизонта hh в точке P, т.е. в главной точке картины.

Точка схода перспективы вторичной проекции a_T также находится в точке P, поскольку для её нахождения используется тот же луч, проведённый из точки S параллельно a_T (a_T||a). Более того, если возьмём прямую b, расположенную в предметной плоскости Τ перпендикулярно Π_K, то вторичная проекция b_T≡b, начальные точки В_H≡В_О и находятся на основании OO картины. Точки схода перспектив бесконечно удалённых точек на b и b_T,тоже расположены в точке P.

Перспективы прямых a и b и их вторичных проекций a_T и b_T находим, соединяя начальные точки A_H, A_О, В_H≡В_О с главной точкой P картины.

Следовательно перспективы прямых, перпендикулярных картинной плоскости (в том числе расположенных в предметной плоскости), имеют одну единственную точку схода, совпадающую с главной точкой P картины.