2.2. Параллельное освещение

Параллельное освещение характеризуется параллельностью направления лучей света относительно друг друга (естественное освещение, например от солнца). Для построения теней необходимо знать направление лучей света в пространстве и их вторичные проекции на предметной плоскости. Ограничимся рассмотрением направления потока параллельных лучей света под некоторым углом сверху вниз. Это означает, что относительно картинной плоскости Π_K и точки зрения S лучи света могут быть направлены: слева направо, спереди слева, спереди, спереди справа, справа налево, сзади справа, сзади и сзади слева.

Пусть поток световых лучей направлен слева направо, следовательно, параллельно картиной плоскости Π_K. Такие лучи света не имеют точек пересечения с Π_K (начальные точки) и точек схода своих перспектив. Тогда луч света можно задать двумя случайными точками A и B на нём (рис. 2.5, а), а его вторичную проекцию точками A_T и B_T.

Естественно, что построенные перспективы A_KB_K луча света и A_KBB_KB его вторичной проекции соответственно параллельны самому лучу и его вторичной проекции. На картинной плоскости Π_K (рис. 2.5, б), расположенной фронтально, показаны выполненные построения перспектив A_KB_K и A_KBB_KB.

Очевидно, что любые световые лучи, параллельные отрезку прямой

AB, будут иметь перспективы, параллельные A_KB_K. Перспективы вторичных проекций этих лучей будут параллельны A_KBB_KB. Такой же вывод можно сделать, когда поток световых лучей направлен справа налево.

Во всех других случаях направления потоков параллельных лучей света их перспективы имеют общую «воздушную» или «земную» точку схода F₁, а перспективы их вторичных проекций имеют общую точку схода F₂, расположенную всегда на линии горизонта hh (см. п.2 раздела 1.2). При этом точки схода F₁ и F₂ находятся на одном перпендикуляре к линии горизонта hh.

1. Тень от точки. При построении тени от точки на картинной плоскости Π_K должны быть заданы или построены точки схода F₁ и F₂ перспектив параллельных лучей света и их вторичных проекций, а также перспективы A_K и A_KB точки A и её вторичной проекции A_T (рис. 2.6) кроме случаев, когда световые лучи идут слева или справа параллельно Π_K (рис. 2.6, а, д).

На рис. 2.6 представлено построение тени от точки A на картиной плоскости Π_K при любых возможных направлениях потоков параллельных лучей света.

Наиболее просты и чаще всего реализуются способы построения тени, когда поток параллельных световых лучей идёт параллельно картинной плоскости Π_K слева (рис. 2.6, а) или справа (рис. 2.6, д).

Построение перспективного изображения тени A₀ от точки A показаны для наиболее часто встречающихся случаев направления лучей света, когда они идут: спереди слева (рис. 2.6,б), спереди справа (рис. 2.6,г), сзади справа (рис. 2.6, е), сзади слева (рис. 2.6, з).

Непосредственное построение тени от точки A, когда световой луч имеет направление спереди или сзади (рис. 2.6, в, ж), невозможно. Для решения задачи параллельным переносом сдвигаем вправо или влево от линии F₁F₂ на некоторое расстояние перспективы A_K и A_KB точки A и её вторичной проекции A_T, например в положение и . Далее определяем мнимую тень и параллельным переносом находим тень A₀ от точки A в исходном положении.

2. Тень от прямой и кривой линии, от плоскости. При построении теней от прямой или кривой лини и других объектов на картинной плоскости Π_K нужно построить или иметь перспективы этих объектов и их вторичных проекций. Кроме того, если освещение объекта осуществляется слева или справа относительно точки зрения S параллельно картинной плоскости Π_K, то стрелками указывают направление лучей света и их вторичных проекций. Для других случаев направления лучей света необходимо задать расположение точек схода F₁ и F₂ перспектив параллельных между собой лучей света и их вторичных проекций.

2.1. Тень от прямой. Предположим, что на картинной плоскости Π_K задана перспектива A_KB_K вертикального стержня AВ, точка B которого лежит на предметной плоскости T (рис. 2.7, а). Требуется построить перспективу падающей тени от стержня AB при заданном направлении потока параллельных лучей света r и его вторичных проекций r_T.

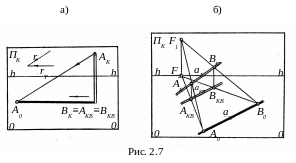Прежде всего, отметим, что вторичная проекция r_T а, следовательно, и её перспектива показывают под каким углом плоскость, образованная лучом света r и его вторичной проекцией r_T, расположена к картинной плоскости Π_K. В данном примере имеем параллельное освещение стержня справа параллельно плоскости Π_K.

Перспективное изображение тени от точки A находится в точке A₀ пересечения прямых, проведённых через точки A_K и A_KB соответственно параллельно r и r_T. Так как B_K совпадает с B_KB, то отрезок A₀B_K есть перспектива падающей тени от стержня AB.

Пусть требуется построить перспективу падающей тени от отрезка AB прямой a при освещении спереди слева (рис. 2.7, б), если на картинной плоскости Π_K заданы перспективы a_K, A_KB_K и a_KB, A_KBB_KB соответственно прямой общего положения, отрезка AB и их вторичных проекций.

На плоскости Π_K левее перспективы a_K прямой a задаём точки схода F₁ и F₂ перспектив параллельных лучей света и их вторичных проекций. Для освещения прямой сверху нужно задать «воздушную» точку схода F₁, выше лини горизонта hh. Точку схода F₂ задаём на одном перпендикуляре с точкой F₁на линии горизонта hh.

После построений перспектив A₀ и B₀ по изложенной выше методике, находим перспективное изображение тени A₀B₀ от отрезка AB прямой a.

2.2. Тень от кривой линии и плоскости. Перспективу тени от кривой линии и от плоскости строят по большему количеству выбранных характерных точек на них, определяя перспективы как точек, так и их вторичных проекций и, задаваясь направлением потока параллельных лучей света.

На практике, как правило, в целом ряде случаев отпадает необходимость строить перспективу вторичной проекции объекта, поскольку перспективы вторичных проекций характерных точек расположены на картинной плоскости в логически объяснимых местах.

При построении перспективных изображений кривых линий стремятся все построения выполнять, не прибегая к совмещению с картинной плоскостью Π_K изображения кривой линии. Так, при построении перспективы окружности, используют, применяемый в аксонометрии способ построения эллипса по восьми точкам, по известным сопряженным диаметрам. Если рассматривать эллипс как перспективное изображение окружности, то можно считать сопряженные диаметры эллипса перспективами двух взаимно перпендикулярных диаметров изображаемой окружности.

Для эллипса, построенного в изометрии, сопряжёнными диаметрами являются отрезки 15 и 37, на концах которых строят параллелограмм (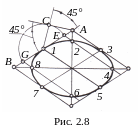 ромб), стороны которого параллельны соответствующим диаметрам (рис. 2.8). Затем из вершины A и середины (точка 1) стороны AB проводят прямые под углом 45° до пересечения в точке C. Из точки 1 радиусом 1С проводят полуокружность до пересечения с AB в точках E и G. Из точек E и G проводят прямые, параллельно сторонам параллелограмма, и на пересечении их с диагоналями находят точки 2, 4, 6 и 8 эллипса. Прямые, проходящие через точки 2, 4 и 6, 8 идентичны таким же прямым, изображенным на рис. 1.32.

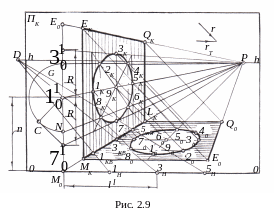Рассмотрим построение перспективы тени от окружности в виде отверстия, расположенного в вертикальной плоскости, которая перпендикулярна картиной плоскости Π_K (рис. 2.9). Плоскость в виде прямоугольника задана перспективой E_KQ_KL_KM_K, сторона LM которого расположена в предметной плоскости. Требуется построить перспективу падающей тени от окружности с радиусом, равным R, перспектива центра которой находится в точке 9_K на расстоянии l и n соответственно от картинной Π_K и предметной T плоскостей. Построить также перспективы собственной и падающей теней от плоскости прямоугольника EQLM.

Сначала построим перспективу окружности, предварительно описав относительно неё квадрат со сторонами, параллельными соответствующим сторонам плоскости прямоугольника EQML. Стороны квадрата, параллельные плоскости T , как и другие прямые им параллельные, имеют точку схода перспектив в главной точке P картины. Продолжим перспективы сторон M_KL_K и E_KQ_K до пересечения с картинной плоскостью Π_K и соединим прямой полученные начальные точки E₀ и M₀. Отрезок прямой E₀M₀ есть высота заданного прямоугольника.

Используя масштаб высот, от точки M₀ отложим отрезок M₀ , равный n, и от точки вверх и вниз отрезки, равные радиусу R окружности, определим точки и . Начальные точки , и соединяем прямыми с точкой P.

Применяя масштаб глубин, от начальной точки M₀ на основании картины OO откладываем отрезок M₀3_H , равный l, и от точки 3_H в обе стороны откладываем отрезки, равные радиусу R окружности, получая точки 1_H и 5_H. Воспользуемся дистанционной точкой D на линии горизонта hh и соединим её прямыми с начальными точками 1_H , 3_H и 5_H. Прямые D1_H, D3_H и D5_H являются перспективами параллельных прямых, расположенных в предметной плоскости и наклонённых под углом 45° к плоскости Π_K, с точкой схода D. Из точек 1_KB, 3_KB и 5_KB пересечения этих прямых с перспективой M_KL_K стороны прямоугольника восстановим перпендикуляры. Точки пересечения их с перспективами P , P и P являются перспективами центра 9_K окружности, 1_K5_K и 3_K7_K – сопряженных диаметров и описанного вокруг окружности квадрата.

Для нахождения недостающих перспектив 2_K, 4_K, 6_K и 8_K четырёх точек эллипса применим рассмотренный на рис. 2.8 способ. Отрезок является натуральной величиной стороны квадрата, а точка его серединой. Поэтому из точек и проводим прямые под углом 45° до пересечения в точке C. Радиусом C из точки проводим полуокружность и на пересечении с отрезком прямой находим точки N и G. Соединяем эти точки с главной точкой P картины прямыми и на пересечении их с диагоналями перспективы квадрата находим искомые перспективы 2_K, 4_K, 6_K и 8_K точек эллипса.

Перспективу падающей тени отверстия круглой формы строим по точкам, путём проведения через перспективу каждой точки и её вторичной проекции прямых, соответственно параллельных направлениям r и r_T до их пересечения. Так, например, перспективой тени от точки 3_K с перспективой вторичной проекции 3_KB будет точка 3₀. Таким образом, перспективой тени от кривой линии в виде окружности будет эллипс1₀2₀…8₀.

Очевидно, перспектива падающей тени от плоскости прямоугольника с круглым отверстием ограничена контуром четырёхугольника E₀Q₀L_KM_K и контуром эллипса 1₀2₀…8₀. Поскольку плоскость прямоугольника освещается слева направо, то собственная тень расположится между контурами E_KQ_KL_KM_K и 1_K2_K…8_K.

3. Тень от пространственного объекта. Рассмотрим последовательность построения границы контуров собственной и падающей тени от пространственных объектов простейших геометрических тел (параллелепипеда, пирамиды, цилиндра и др.). Одновременно, при необходимости, остановимся на основных моментах построения их перспективных изображений.

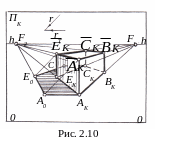3.1. Параллелепипед. Предположим, что на картинной плоскости Π_K (рис. 2.10) задано изображение прямого параллелепипеда, построенного с применением способа перспективных масштабов и масштабных точек (см. п. 3 раздела 1.6, рис. 1.41).

При освещении справа налево параллельно плоскости Π_K требуется построить собственную и падающую тень от параллелепипеда с нижним основанием ABCE, лежащим в предметной плоскости Τ.

Через перспективы , , , и A_K, B_K, C_K, E_K вершин верхнего и нижнего оснований параллелепипеда проводим прямые, соответственно параллельные лучам света r и вторичным проекциям r_T, до их пересечения. Ломаная линия A_KA₀E₀C₀C_K является контуром падающей тени. Четырёхугольник A_K E_K есть контур видимой части собственной тени.

3.2. Пирамида. Пусть требуется построить собственную и падающую тень от правильной четырёхугольной пирамиды с основанием, произвольно расположенным на картинной плоскости Π_K, сторона основания которого равна a и высота n (рис. 2.11). Примем освещение слева направо параллельно плоскости Π_K. Направление потока световых лучей и их вторичных проекций заданы стрелками r и r_T.

Прежде всего отметим, что в связи с произвольным расположением основания пирамиды относительно Π_K, точки схода перспектив его сторон неизвестны. Поэтому на плоскости помимо главной точки P картины зададим перспективу A_K вершины основания пирамиды и перспективу A_KF₁ прямой произвольного направления.

Дальнейшие построения выполняем с применением способа перспективных масштабов и масштабных точек. Тогда относительно совмещённой с Π_K точки зрения S и точки схода F₁ перспектив параллельных сторон основания, одна из которых проходит через точку A,

построим угол 90° и на линии горизонта найдём точку схода F₂ перспектив двух других параллельных сторон. Точки S и P должны быть расположены на одном перпендикуляре к линии hh. Соединим точки A_K и F₂ прямой.

На линии горизонта hh находим масштабные точки M₁ и M₂. Для этого из точек схода F₁ и F₂ радиусами, соответственно равными F₁S и F₂S, проводим дуги окружностей.

Соединяем точку A_K с точками M₁ и M₂ прямыми до пересечения их с основанием OO картины в точках A_H и M_H. На линии OO от точек A_H и M_H откладываем отрезки A_HB_H и M_HE_H, равные стороне a квадрата основания. Полученные точки B_H и E_H соединяем прямыми с точками M₁ и M₂. На пересечении этих прямых с перспективами A_KF₁ и A_KF₂ находим перспективы B_K и E_K вершин основания.

Используя точки схода F₁ и F₂ перспектив параллельных сторон основания пирамиды, проводим прямые B_KF₂ и E_KF₁, на пересечении которых находим перспективу C_K четвёртой невидимой вершины основания.

Для построения перспективы G_K вершины пирамиды из главной точки P картины проводим прямую, например в левый нижний угол рамки картинной плоскости П_K, до пересечения с основанием OO картины, отмечая точку N_H, от которой по вертикали вверх откладываем отрезок N_HN, равный высоте n пирамиды. Соединяем точку N с точкой Р. Из точки G_KB пересечения диагоналей основания A_KB_KC_KE_K проводим горизонтальную прямую до пересечения с прямой PN_H в точке К, из которой поднимаем вертикаль до пересечения с прямой PN в точке L. Отрезок KL соответствует высоте n пирамиды и определяет положение перспективы G_K вершины пирамиды. Точку G_K соединяем прямыми с точкам A_K, B_K, C_K и E_K, получая в результате перспективу пирамиды.

При построении перспективы падающей тени от пирамиды сначала находим перспективу G₀ тени от её вершины. Затем точку G₀ соединяем прямыми с точками A_K и C_K. Видимая часть собственной тени ограничена контуром треугольника A_KB_KG_K. Перспектива падающей тени находится внутри контура ломаной линии A_KG₀C_KB_KA_K.

3.3. Цилиндр. Рассмотрим построение перспектив собственной и падающей теней от прямого кругового цилиндра с нижним основанием в виде окружности с диаметром 2R, лежащим в произвольном месте на предметной плоскости (рис. 2.12). На картинной плоскости Π_K зададим точки схода F₁ и F₂ перспектив лучей света и их вторичных проекций при параллельном освещении слева сзади. Высоту цилиндра принимаем равной l.

Вначале построим перспективу цилиндра. Используем для этого способ применения дистанционной точки D. Построение перспективы начинаем выполнять с нижнего основания, предварительно описав относительно окружности квадрат. Однако, в отличие от изложенного в п. 4 раздела 1.5, построение перспективы будем осуществлять без совмещения изображения окружности на предметной плоскости с картинной плоскостью.

На плоскости Π_K выбираем местоположение перспективы Q_K центра окружности. Через точку Q_K и главную точку P картины проводим прямую до пересечения с основанием OO картины в точке 1_H. От точки 1_H на линии OO в обе стороны откладываем отрезки 1_H3_H и 1_H7_H, равные радиусу R окружности и соединяем точки 3_H и 7_H с точкой P. Поскольку прямые, перспективы которых 3_HP и 7_HP параллельны между собой и перпендикулярны плоскости Π_K, то отрезок прямой 3_H7_H является натуральной величиной диаметра, перспектива которого 3_K7_K.

Соединяем прямыми перспективу Q_K с дистанционными точками D ₁ и D₂. На пересечении их с перспективами 3_HP и 7_HP находим перспективы A_K, B_K, C_K и E_K квадрата, описанного относительно окружности основания цилиндра. Одновременно находим перспективы 1_K, 3_K, 5_K и 7_K точек окружности, касательных к сторонам квадрата.

Для нахождения ещё четырёх перспектив 2_K, 4_K, 6_K и 8_K точек на окружности используем приём, рассмотренный на рис. 2.8. Из точек A_K и 1_K, являющейся серединой отрезка A_KB_K, под углом 45° навстречу друг другу проводим прямые до пересечения в точке V. Далее из точки 1_K радиусом 1_KV проводим дугу окружности до пересечения с отрезком A_KB_K в двух точках, которые соединяем прямыми с точкой P. На пересечении этих прямых с диагоналями перспективы квадрата A_KB_KC_KE_K находим точки 2_K, 4_K, 6_K и 8_K эллипса.

Все точки окружности верхнего основания цилиндра расположены на расстоянии l от предметной плоскости. Следовательно начальные точки вспомогательных прямых, проведённых через точки , ,…, под углом 45° и перпендикулярно к картинной плоскости Π_K, будут лежать на линии, параллельной OO, на расстоянии l от неё.

Заметим, что в данном случае нет необходимости строить перспективу квадрата, описанного относительно окружности верхнего основания. Достаточно ограничиться нахождением начальных точек только тех прямых, которые перпендикулярны плоскости Π_K (эти прямые не показаны). При построении перспективы таких прямых соединяют прямыми начальные точки с точкой P, на пересечении которых с вертикалями, проведенными из одноимённых перспектив точек окружности нижнего основания, находим перспективы , ,…, точек окружности верхнего основания.

Так, например, для прямой, проведённой через точку _K окружности верхнего основания, начальной точкой будет точка ₀, расположенная на одном перпендикуляре с точкой 1_H. На пересечении перспективы ₀ P этой прямой с вертикалями, проведёнными из точек 1_K и 5_K, находим перспективы и . Аналогичным образом находим перспективы других точек окружности верхнего основания.

После соединения найденных перспектив точек нижнего и верхнего оснований цилиндра плавной кривой линией по лекалу, с учётом их видимости, и касательных к эллипсам (очерковые образующие), приступаем к построению перспективы собственной и падающей тени от цилиндра.

К перспективе нижнего основания из точки схода F₂ проводим две касательные, являющиеся вторичными проекциями лучей света и находим точки касания M и N. Из этих точек проводим образующие M и N поверхности цилиндра. Очевидно перспектива собственной тени на поверхности цилиндра ограничена контуром, составленным из образующих M , N и дугами эллипсов между ними.

Через точки и M, и 2_K, … и N также проводим прямые к точкам схода F₁ и F₂, в точках пересечения которых найдём перспективы падающих теней от точек, расположенных на окружности верхнего основания. Таким образом, перспективное изображение падающей тени от цилиндра находится внутри контура MM₀2₀…N, ограниченного дугой M2_K3_K…N эллипса нижнего основания.

3.4. Конус. При заданных точках схода F₁ и F₂ перспектив лучей света и их вторичных проекций параллельного освещения справа сзади прямого кругового конуса с основанием, расположенным на предметной плоскости и высотой l, требуется построить перспективное изображение собственной и падающей тени от конуса. Пусть необходимо задать расположение перспективы Q_K центра окружности основания конуса с диаметром, равным 2R, на картинной плоскости Π_K по своему усмотрению.

Для решения задачи воспользуемся методикой построения перспективы окружности нижнего основания прямого кругового цилиндра (см. рис. 2.12). В результате выполненных построений с использованием дистанционной точки D находим перспективу окружности основания конуса (рис. 2.13).

Вершина G конуса отстоит на расстоянии l от предметной плоскости, а следовательно и от основания OO картины. Для нахождения перспективы G_K вершины конуса используем дистанционную точку D, которая является точкой схода перспектив параллельных прямых, наклонённых к плоскости П_К под углом 45°. Поэтому параллельные прямые, проходящие через центр Q и точку B описанного вокруг окружности основания квадрата, и через вершину G конуса, имеют начальные точки соответственно 9_H и _H. Перспектива G_K вершины конуса находится в точке пересечения перспективы _HD прямой с перпендикуляром, восстановленным из точки Q_K. Как видно из рис. 2.13 построения, выполненные по масштабу высот, дают тот же результат.

Для нахождения перспективы собственной и падающей тени от конуса прежде всего необходимо на картинной плоскости Π_K задать расположение точек схода F₁ и F₂ перспектив соответственно лучей света и их вторичных проекций. Причём точки F₁ и F₂ должны быть расположены на одном перпендикуляре к основанию OO картины и слева от главной точки P. При этом точка схода F₂ должна лежать на линии горизонта hh, а F₁ – ниже её. Чем больше расстояние F₁ F₂, тем под большим углом к предметной плоскости направлен поток параллельных лучей света.

Сначала построим перспективу G₀ тени от вершины G конуса. Тень G₀ находится в точке пересечения прямых, проведённых из точки F₁ в точку G_K и из точки F₂ в точку Q_K. Из точки G₀ проводим касательные к основанию (эллипсу), и находим точки M и N касания. Поверхность конуса, расположенная между образующими MG_K и NG_K и дугой M7_K6_K5_KN эллипса, есть перспектива собственной тени. Перспектива падающей тени ограничена контуром MG₀N и той же дугой эллипса.

3.5. Сфера. Построение перспективного изображения собственной и падающей тени от сферической поверхности является довольно трудоёмким процессом. Связано это с тем, что перспектива сферы, расположенной в предметном пространстве за картинной плоскостью, есть эллипс или, в крайне редко встречающемся случае, – окружность. В этом легко убедиться.

На рис. 2.14 для построения перспективы сферы на картинной плоскости Π_K из точки зрения S проводим проецирующие лучи, касательные к поверхности сферы, которые в совокупности образуют коническую поверхность вращения. При пересечении поверхности конуса плоскостью Π_K, расположенной под острым углом к оси вращения, получим перспективу сферы в виде эллипса. Лишь в частном случае, когда центр сферы будет расположен на продолжении главного луча SP, в перспективе будем иметь окружность.

Из чисто психологических соображений изображение сферы в виде эллипса не воспринимается человеком. Поэтому на картинной плоскости, без крайней необходимости, сферу изображают в виде окружности. Рассмотрим приближённый способ аппроксимации перспективного изображения сферы в виде эллипса на окружность, а также те особенности, которые возникают при построении перспективы собственной и падающей тени.

Предположим, что сфера расположена внутри прямого кругового цилиндра того же диаметра с основанием, лежащим на предметной плоскости.

На рис. 2.15 построена перспектива такого цилиндра по методике, применённой в разделе 2.2, рис. 2.12, но без построения изображения верхнего основания. Перспектива квадрата, описанного вокруг окружности нижнего основания, есть A_KB_KC_KE_K. Диаметр цилиндра равен 2R.

Построим перспективу сферы, вписанную в цилиндр и опирающуюся на предметную плоскость в точке Q. По масштабу высот находим перспективу центра сферы, из которого описываем окружность так, чтобы

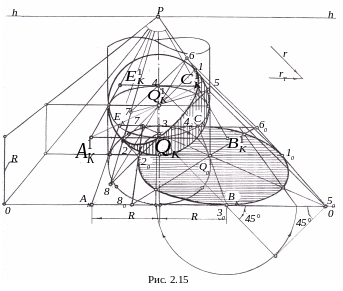
перспективы очерковых образующих цилиндра были касательными к ней. Отметим, что радиус R сферы равен половине расстояния между перспективами очерковых образующих цилиндра. При смещении перспективы Q_K влево от главной точки P картины центр сферы имеет тенденцию смещаться влево по горизонтали, а при смещении в противоположную сторону – вправо. В этих случаях необходимо вносить корректировку расположения центра сферы относительно перспективы центра Q_K нижнего основания цилиндра, что объясняется принятыми допущениями при аппроксимации.

Считаем также, что ортогональной проекцией сферы на предметную плоскость является окружность (в перспективе – эллипс с центром в точке Q_K ).

Далее строим перспективу горизонтально расположенного экватора (окружности) сферы с центром в точке , предварительно построив перспективу , описанного вокруг него квадрата.

При заданном направлении потока лучей света r и их вторичных проекций r_T освещения слева направо параллельно картинной плоскости к перспективам очерка сферы и её экватору проводим касательные, соответственно параллельные r и r_T, определяя точки касания 1, 2, 3 и 4. Эти точки расположены на серединах сторон квадрата 5678, стороны 56 и 78 которого перпендикулярны, а стороны 58 и 67 параллельны к Π_K.

Вторичной проекцией перспективы квадрата является перспектива A_KB_KC_KE_K квадрата нижнего основания цилиндра. Более того, фигура 5678 конгруэнтна фигуре . Поэтому перспектива 5₀6₀7₀8₀ есть падающая тень от перспективы квадрата 5678, описанного вокруг контура (окружности) собственной тени.

Контур перспективы падающей тени будет эллипс, вписанный в фигуру 5₀6₀7₀8₀. Построение эллипса осуществим по восьми его точкам, из которых точки 1₀, 2₀, 3₀ и 4₀ найдём на пересечении прямых, параллельных направлению лучей света r, проведённых из точек 1, 2, 3 и 4, с соответствующими сторонами перспективы5₀6₀7₀8₀. Остальные точки (цифрами не обозначены) найдём, используя тот же самый приём, показанный на рис. 2.15.

Таким образом, перспективой падающей тени от сферы является плоская фигура, ограниченная контуром построенного эллипса.

Плоскость квадрата 5678 перпендикулярна потоку параллельных лучей света r. Поэтому эллипс, вписанный в этот квадрат будет являться контуром собственной тени. Однако из-за принятых допущений при аппроксимации могут возникнуть значительные перспективные искажения. Поэтому ограничимся построением дуги эллипса лишь на видимой части поверхности сферы, используя известный из аксонометрии приём построения эллипса по его большой оси (отрезок 12) и дополнительной точке 3 (см. раздел 7, часть 1).

3.6. Тор. Методику построения перспективы собственной и падающей тени от тора рассмотрим на примере закрытой торовой поверхности, полученной вращением образующей l в виде дуги окружности радиуса R вокруг оси i. На рис. 2.16 показана фронтальная проекция тора. При рассечении его плоскостями Σ, Τ и Г образуются окружности с соответствующими диаметрами d₁, d₂ и d₃.

Предварительно строим перспективу поверхности тора. Сущность методики сводится к построению перспектив окружностей, расположенных на расстояниях n₁, n₂ и n₃ от окружности основания, диаметр которой равен d. Перспективы окружностей будем строить с помощью описанных вокруг них квадратов. Как и в предыдущих случаях, задаваясь расположением перспективы Q_K окружности нижнего основания на картинной плоскости Π_K, соединяем её прямой с главной точкой P картины и на основании OO находим точку 4_H пересечения. Соединяем точку Q_K с дистанционной точкой D прямой, на пересечении её с перспективами A_HP и B_HP находим точки B_K и E_K. Фигура A_KB_KC_KE_K есть перспектива I квадрата, описанного вокруг окружности с центром Q.

Перспективы и находим на одном перпендикуляре к Q_K по способу масштаба высот с помощью фронтальной проекции тора. Перспективы II, III и IV квадратов построим аналогичным образом. Впишем в перспективы I, II, III и IV квадратов эллипсы по восьми точкам, которые являются перспективами соответствующих окружностей тора. Находим также перспективу верхней точки тора.

К построенным эллипсам из точки слева и справа проводим перспективы очерковых касательных, получая в результате перспективу тора.

Для построения перспективы собственной тени зададим направление потока световых лучей r и их вторичных проекций r_T слева направо, параллельно картинной плоскости Π_K. Рассечём поверхность тора секущими плоскостями Φ, Ψ и Ω параллельными плоскости Π_K. Так, плоскость Φ рассечёт эллипсы с центрами Q_K, и по хордам a, b, c и коснётся эллипса с центром в точке 5. Последовательно соединив точки на концах этих хорд и точку 5 плавной кривой линией, получим перспективу линии пересечения поверхности тора плоскостью Φ. Аналогичным способом находим линии пересечения поверхности тора плоскостями Ψ и Ω.

Проводим касательные, параллельные лучам света r, к перспективам очерковой образующей тора и найденным линиям пересечения, определяя точки касания 1_K, 2_K, 3_K и 4_K. Соединяя эти точки плавной кривой линией, находим линию контура собственной тени на поверхности тора. Для более точного построения контура собственной тени необходимо взять большее количество секущих плоскостей.

Перспективы вторичных проекций точек 1, 2, 3 и 4 расположены на соответствующих хордах, поэтому легко находим перспективы 1₀, 2₀, 3₀ и т. д. падающих теней от этих точек (на рис. 2.16 не показаны), соединяя которые кривой линией по лекалу, находим контур падающей тени от тора.

С помощью рассмотренного способа можно построить перспективы различного вида поверхностей тора и контуров собственной и падающей теней. Более того, данный способ можно рекомендовать для получения перспективных изображений различных по форме поверхностей вращения и теней от них.