8. Приближенное дифференцирование функций

1. Цель работы

Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу» Приближенное дифференцирование», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.

2. Задание

Построить зависимости производных первого и второго порядка от аргумента в диапазоне 1..10 с единичным шагом.

Определить оптимальное значение шага, обеспечивающее минимальную погрешность приближенных расчетов производных первого и второго порядков для x=3.

Примеры заданий:

y=5x5+4x3 y=x4 y=ex y=2x3+x4 y=x3+x5

y=x5 y=x2+x4 y=x3+x4 y=e2x y=x3

8.3 Теоретические сведения

Задача приближенного дифференцирования возникает для сложных аналитических функций или функций , заданных дискретными данными. Функция приближенно описывается интерполяционным полиномом, дифференцирование которого не вызывает трудностей.

Таблица 8.1

xi	yi	Δy	Δ2y	Δ3y	Δ4y	Δ5y
x0	y0	Δy0	Δ2y0	Δ3y0	Δ4y0	Δ5y0
x1	y1	Δy1	Δ2y1	Δ3y1	Δ5y1
x2	y2	Δy2	Δ2y2	Δ3y2
x3	y3	Δy3	Δ2y3
x4	y4	Δy4
x5	y5

Представим любую исходную функцию в виде таблицы 8.1 соответствующих значений x_i и y_i и конечных разностей Δy_i , Δ²y_i, Δ³y_i….В таблице конечные разности различных порядков рассчитываются по формулам

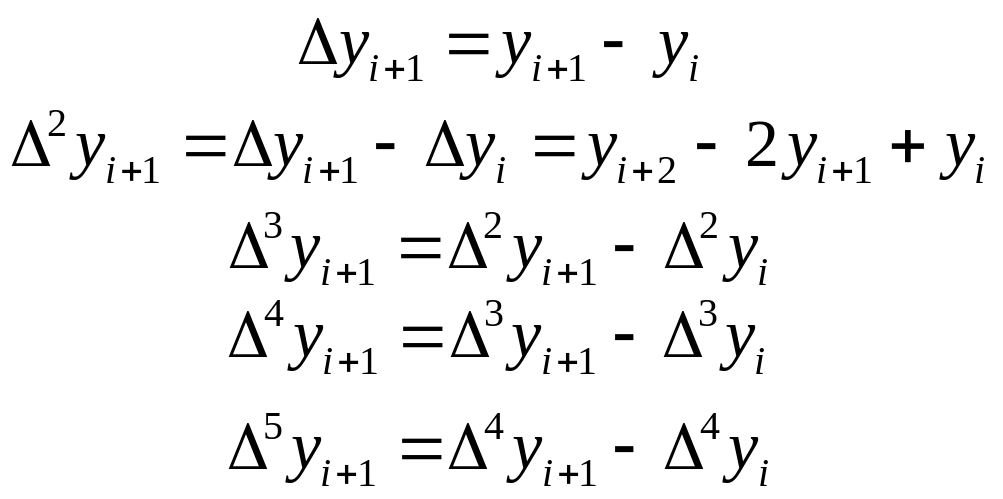(8.1)

Запишем интерполяционный полином в форме Ньютона :

(8.2)

Продифференцируем (8.2) по x :

(8.3)

Продифференцируем (8.3) по x :

(8.4)

При x=x₀

(8.5)

Ограничиваясь только первым членом в разложениях ,получим

; (8.6)

В случае h=1 формулы еще больше упрощаются и производные численно равны соответствующим конечным разностям

; (8.7)

При уменьшении величины шага погрешность расчетов уменьшается. Наилучшая точность , которая может быть достигнута при уменьшении шага по оси x , определяется погрешностью округления, зависящей от используемого программного и аппаратного обеспечения.

Если при расчетах производных не ограничиваться только первыми членами суммы, то можно получить более точные формулы для расчета производных, учитывающие информацию не только о соседней, но и о более удаленных точках.

Для двух слагаемых( трехточечная схема) формулы (8.5) можно привести к виду

(8.8)

Можно получить ещё более точные формулы, использую информацию о большем количестве точек. В этих случаях интерполяционный полином удобнее записывать в форме Лагранжа .

Для пятиточечной системы имеем

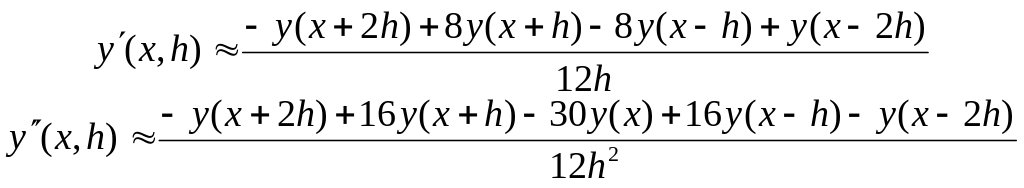(8.9)

Р ассмотрим функцию

. (8.10)

При x=0.5 и h=0.01 получаем

Процедура определения производной в Mathcad дает значения

Рис.8.1 Графики функции (8.10) и её производных

На рисунке 8.1 показаны графики при x=0..2 при шаге h=0.01.

Результаты расчетов в зависимости от шага h имеют различную относительную ошибку.

lg(Δ)

-1

-3

-5

-7

Рис. 8.2

На рисунке 8.2 показана зависимость абсолютной ошибки первой производной от величины шага h для функции y(x)=x³ при x=3.

При шаге h=10^-8достигается минимальная ошибка вычислений . Методическая погрешность убывает с уменьшением шага. При этом погрешность округления с уменьшением шага увеличивается, поэтому оптимальная величина суммарной погрешности вычислений достигается при h=10^-8.

Для численного дифференцирования в Mathcad используется метод Риддера, в котором для оценки точности производной последовательно определяются конечные разности высоких порядков. Максимальная степень оператора однократного вычисления производной равна пяти.

Для вычисления производных порядка >5 следует использовать смешенную запись.

Для получения производной в символьном виде нужно записать оператор численного определения производной и затем поставить знак → из меню символьных вычислений , также можно использовать команду «Дифференцировать» из меню Символика.