Вариант № 5

1.  Най­ди­те зна­че­ние вы­ра­же­ния  .

2.  Най­ди­те сумму чисел   и  .

3. Тет­радь стоит 40 руб­лей. Какое наи­боль­шее число таких тет­ра­дей можно будет ку­пить на 950 руб­лей после по­ни­же­ния цены на 25%?

4.  Най­ди­те   из ра­вен­ства   если   и 

5. Най­ди­те зна­че­ние вы­ра­же­ния  .

6.  Вы­пуск­ни­ки 11а по­ку­па­ют бу­ке­ты цве­тов для по­след­не­го звон­ка: из 3 роз каж­до­му учи­те­лю и из 7 роз класс­но­му ру­ко­во­ди­те­лю и ди­рек­то­ру. Они со­би­ра­ют­ся по­да­рить бу­ке­ты 15 учи­те­лям (вклю­чая ди­рек­то­ра и класс­но­го ру­ко­во­ди­те­ля), розы по­ку­па­ют­ся по опто­вой цене 35 руб­лей за штуку. Сколь­ко руб­лей стоят все розы?

7.  Ре­ши­те урав­не­ние  . В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

8. Пря­мая   па­рал­лель­на ка­са­тель­ной к гра­фи­ку функ­ции  . Най­ди­те абс­цис­су точки ка­са­ния.

9.  Уста­но­ви­те со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми зна­че­ни­я­ми: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го столб­ца.

 

ВЕ­ЛИ­ЧИ­НЫ		ВОЗ­МОЖ­НЫЕ ЗНА­ЧЕ­НИЯ
А) длина хо­бот­ка мухи Б) длина эк­ва­то­ра В) длина то­вар­но­го по­ез­да Г) тор­моз­ной путь ав­то­мо­би­ля		1) 40 000 км 2) 100 м 3) 0,2 см 4) 1,5 км

 

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

A	Б	В	Г

10.  В сред­нем из 1300 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 13 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

11.  Ко­эф­фи­ци­ент по­лез­но­го дей­ствия (КПД) кор­мо­за­пар­ни­ка равен от­но­ше­нию ко­ли­че­ства теп­ло­ты, за­тра­чен­но­го на на­гре­ва­ние воды мас­сой   (в ки­ло­грам­мах) от тем­пе­ра­ту­ры   до тем­пе­ра­ту­ры   (в гра­ду­сах Цель­сия) к ко­ли­че­ству теп­ло­ты, по­лу­чен­но­му от сжи­га­ния дров массы  кг. Он опре­де­ля­ет­ся фор­му­лой  , где   Дж/(кг К) – теплоёмкость воды,   Дж/кг – удель­ная теп­ло­та сго­ра­ния дров. Опре­де­ли­те наи­мень­шее ко­ли­че­ство дров, ко­то­рое по­на­до­бит­ся сжечь в кор­мо­за­пар­ни­ке, чтобы на­греть   кг воды от   до ки­пе­ния, если из­вест­но, что КПД кор­мо­за­пар­ни­ка не боль­ше  . Ответ вы­ра­зи­те в ки­ло­грам­мах.

12.  Рей­тин­го­вое агент­ство опре­де­ля­ет рей­тинг со­от­но­ше­ния «цена-ка­че­ство» мик­ро­вол­но­вых печей. Рей­тинг вы­чис­ля­ет­ся на ос­но­ве сред­ней цены P и оце­нок функ­ци­о­наль­но­сти F, ка­че­ства Q и ди­зай­на D. Каж­дый от­дель­ный по­ка­за­тель оце­ни­ва­ет­ся экс­пер­та­ми по 5-балль­ной шкале це­лы­ми чис­ла­ми от 0 до 4. Ито­го­вый рей­тинг вы­чис­ля­ет­ся по фор­му­ле

 

R = 8(F + Q) + 4D − 0,01P.

 

В таб­ли­це даны оцен­ки каж­до­го по­ка­за­те­ля для не­сколь­ких мо­де­лей печей. Опре­де­ли­те, какая мо­дель имеет наи­выс­ший рей­тинг. В от­ве­те за­пи­ши­те зна­че­ние этого рей­тин­га.

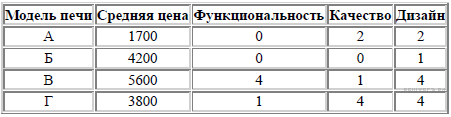
13.  По двум па­рал­лель­ным же­лез­но­до­рож­ным путям в одном на­прав­ле­нии сле­ду­ют пас­са­жир­ский и то­вар­ный по­ез­да, ско­ро­сти ко­то­рых равны со­от­вет­ствен­но 90 км/ч и 30 км/ч. Длина то­вар­но­го по­ез­да равна 600 мет­рам. Най­ди­те длину пас­са­жир­ско­го по­ез­да, если время, за ко­то­рое он про­шел мимо то­вар­но­го по­ез­да, равно 1 ми­ну­те. Ответ дайте в мет­рах.

14.  Най­ди­те точку ми­ни­му­ма функ­ции  .

15. 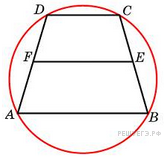  Около тра­пе­ции опи­са­на окруж­ность. Пе­ри­метр тра­пе­ции равен 22, сред­няя линия равна 5. Най­ди­те бо­ко­вую сто­ро­ну тра­пе­ции.

16. 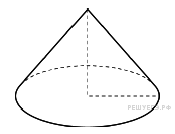  Вы­со­та ко­ну­са равна 4, а диа­метр ос­но­ва­ния равен 6. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

17.  На ко­ор­ди­нат­ной пря­мой от­ме­че­ны точки K, L, M и N.

 

Про число m из­вест­но, что оно равно  .

Уста­но­ви­те со­от­вет­ствие между ука­зан­ны­ми точ­ка­ми и чис­ла­ми из пра­во­го столб­ца, ко­то­рые им со­от­вет­ству­ют.

 

ТОЧКИ		ЧИСЛА
А) K Б) L В) M Г) N		1)  2)  3)  4)

 

Впи­ши­те в при­ведённую в от­ве­те таб­ли­цу под каж­дой бук­вой со­от­вет­ству­ю­щую цифру. 

А	Б	В	Г

18.  Среди вось­ми­класс­ни­ков не­ко­то­рые участ­во­ва­ли в олим­пиа­де по ма­те­ма­ти­ке, а не­ко­то­рые — по об­ще­ст­во­зна­нию. Все те школь­ни­ки, ко­то­рые участ­во­ва­ли в олим­пиа­де по об­ще­ст­во­зна­нию не участ­во­ва­ли в олим­пиа­де по ма­те­ма­ти­ке. Вы­бе­ри­те утвер­жде­ния, ко­то­рые сле­ду­ют из при­ведённых дан­ных.

1) Вось­ми­класс­ник, ко­то­рый участ­во­вал в олим­пиа­де по ма­те­ма­ти­ке не участ­во­вал в олим­пиа­де по об­ще­ст­во­зна­нию.

2) Все вось­ми­класс­ни­ки участ­во­ва­ли в олим­пиа­де либо по ма­те­ма­ти­ке, либо по об­ще­ст­во­зна­нию.

3) Среди тех вось­ми­класс­ни­ков, ко­то­рые участ­во­ва­ли в олим­пиа­де по ма­те­ма­ти­ке есть хотя бы один участ­ник, ко­то­рый участ­во­вал в олим­пиа­де по об­ще­ст­во­зна­нию.

4) Нет ни од­но­го вось­ми­класс­ни­ка, ко­то­рый участ­во­вал и в олим­пиа­де по ма­те­ма­ти­ке и в олим­пиа­де по об­ще­ст­во­зна­нию.

19.  Най­ди­те трёхзнач­ное число, сумма цифр ко­то­ро­го равна 25, если из­вест­но, что его квад­рат де­лит­ся на 16.

20.  В ма­га­зи­не бы­то­вой тех­ни­ки объём про­даж хо­ло­диль­ни­ков носит се­зон­ный ха­рак­тер. В ян­ва­ре было про­да­но 10 хо­ло­диль­ни­ков, и в три по­сле­ду­ю­щих ме­ся­ца про­да­ва­ли по 10 хо­ло­диль­ни­ков. С мая про­да­жи уве­ли­чи­ва­лись на 15 еди­ниц по срав­не­нию с преды­ду­щим ме­ся­цем. С сен­тяб­ря объём про­даж начал умень­шать­ся на 15 хо­ло­диль­ни­ков каж­дый месяц от­но­си­тель­но преды­ду­ще­го ме­ся­ца. Сколь­ко хо­ло­диль­ни­ков про­дал ма­га­зин за год?

Вариант 6

1.  Най­ди­те зна­че­ние вы­ра­же­ния  .

2. Най­ди­те зна­че­ние вы­ра­же­ния  .

3.  Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 13 050 руб­лей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Кон­стан­ти­нов­ны?

4.  В фирме «Эх, про­ка­чу!» сто­и­мость по­езд­ки на такси (в руб­лях) рас­счи­ты­ва­ет­ся по фор­му­ле  , где   — дли­тель­ность по­езд­ки, вы­ра­жен­ная в ми­ну­тах  . Поль­зу­ясь этой фор­му­лой, рас­счи­тай­те сто­и­мость 8-ми­нут­ной по­езд­ки.

5.  Най­ди­те  , если  .

6. На счету На­сти­но­го мо­биль­но­го те­ле­фо­на было 79 руб­лей, а после раз­го­во­ра с Вовой оста­лось 40 руб­лей. Сколь­ко минут длил­ся раз­го­вор с Вовой, если одна ми­ну­та раз­го­во­ра стоит 1 рубль 50 ко­пе­ек?

7.  Най­ди­те ко­рень урав­не­ния  .

8. 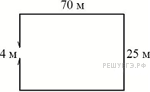  Уча­сток земли имеет пря­мо­уголь­ную форму. Сто­ро­ны пря­мо­уголь­ни­ка 25 м и 70 м. Най­ди­те длину за­бо­ра (в мет­рах), ко­то­рым нужно ого­ро­дить уча­сток, если в за­бо­ре нужно преду­смот­реть во­ро­та ши­ри­ной 4 м.

9. Уста­но­ви­те со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми зна­че­ни­я­ми: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий эле­мент из вто­ро­го столб­ца.

 

ВЕ­ЛИ­ЧИ­НЫ		ВОЗ­МОЖ­НЫЕ ЗНА­ЧЕ­НИЯ
А) пло­щадь го­ро­да Санкт-Пе­тер­бург Б) пло­щадь ла­до­ни взрос­ло­го че­ло­ве­ка В) пло­щадь по­верх­но­сти тум­боч­ки Г) пло­щадь бас­кет­боль­ной пло­щад­ки		1) 364 кв. м 2) 100 кв. см 3) 1399 кв. км 4) 0,2 кв. м

В таб­ли­це под каж­дой бук­вой, со­от­вет­ству­ю­щей ве­ли­чи­не, ука­жи­те номер её воз­мож­но­го зна­че­ния.

A	Б	В	Г

10.  На эк­за­ме­не по гео­мет­рии школь­ник от­ве­ча­ет на один во­прос из спис­ка эк­за­ме­на­ци­он­ных во­про­сов. Ве­ро­ят­ность того, что это во­прос по теме «Три­го­но­мет­рия», равна 0,3. Ве­ро­ят­ность того, что это во­прос по теме «Впи­сан­ная окруж­ность», равна 0,25. Во­про­сов, ко­то­рые од­но­вре­мен­но от­но­сят­ся к этим двум темам, нет. Най­ди­те ве­ро­ят­ность того, что на эк­за­ме­не школь­ни­ку до­ста­нет­ся во­прос по одной из этих двух тем.

11.

Скейт­бор­дист пры­га­ет на сто­я­щую на рель­сах плат­фор­му, со ско­ро­стью   м/с под ост­рым углом  к рель­сам. От толч­ка плат­фор­ма на­чи­на­ет ехать со ско­ро­стью   (м/с), где   кг — масса скейт­бор­ди­ста со скей­том, а   кг — масса плат­фор­мы. Под каким мак­си­маль­ным углом   (в гра­ду­сах) нужно пры­гать, чтобы разо­гнать плат­фор­му не менее чем до 0,3 м/с?

12.

 

В сред­нем граж­да­нин А. в днев­ное время рас­хо­ду­ет 125 кВт ч элек­тро­энер­гии в месяц, а в ноч­ное время — 155 кВт ч элек­тро­энер­гии. Рань­ше у А. в квар­ти­ре был уста­нов­лен од­но­та­риф­ный счет­чик, и всю элек­тро­энер­гию он опла­чи­вал по та­ри­фу 2,5 руб. за кВт ч. Год назад А. уста­но­вил двух­та­риф­ный счeтчик, при этом днев­ной рас­ход элек­тро­энер­гии опла­чи­ва­ет­ся по та­ри­фу 2,5 руб. за кВт ч, а ноч­ной рас­ход опла­чи­ва­ет­ся по та­ри­фу 0,7 руб. за кВт ч.

 В те­че­ние 12 ме­ся­цев режим по­треб­ле­ния и та­ри­фы опла­ты элек­тро­энер­гии не ме­ня­лись.

На сколь­ко боль­ше за­пла­тил бы А. за этот пе­ри­од, если бы не по­ме­нял­ся счет­чик? Ответ дайте в руб­лях.

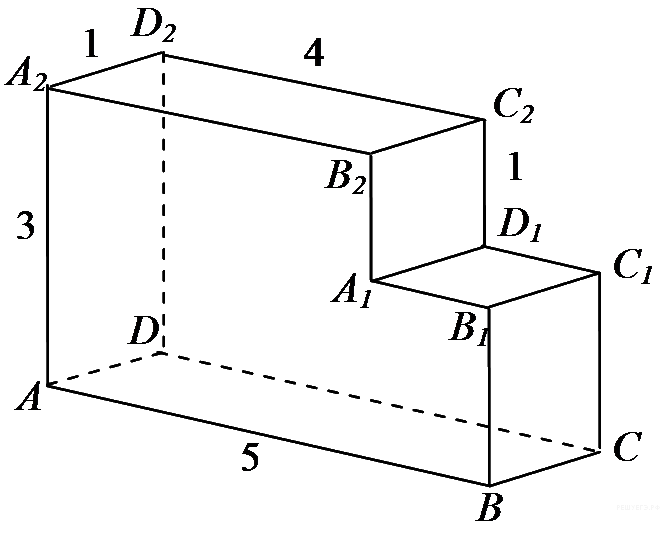
13.   Най­ди­те тан­генс угла   мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

14.  Най­ди­те точку мак­си­му­ма функ­ции 

15. 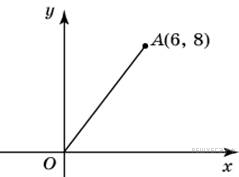  Най­ди­те ор­ди­на­ту се­ре­ди­ны от­рез­ка, со­еди­ня­ю­ще­го точки O (0; 0) и A (6; 8).

16.

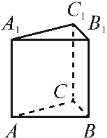
Най­ди­те объём мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки   пра­виль­ной тре­уголь­ной приз­мы   пло­щадь ос­но­ва­ния ко­то­рой равна 9, а бо­ко­вое ребро равно 8.

17.  На пря­мой от­ме­че­но число m и точки K, L, M и N.

 

 

ТОЧКИ		ЧИСЛА
А) K Б) L В) M Г) N		1)  2)  3)  4)

 

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В	Г

18.  Со­глас­но гра­до­стро­и­тель­ным нор­мам, в домах выше 5 эта­жей дол­жен быть уста­нов­лен лифт. Счи­тая, что эти нормы не­укос­ни­тель­но ис­пол­ня­ют­ся, вы­бе­ри­те утвер­жде­ния, ко­то­рые не­по­сред­ствен­но из этого сле­ду­ют.

 

1) Если в доме нет лифта, то он не выше 5 эта­жей.

2) Если в доме 3 этажа, то в нём лифта нет.

3) Если в доме боль­ше 5 эта­жей, то в нём есть лифт.

4) Если в доме есть лифт, то он выше 5 эта­жей.

 

В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

19.  При­ве­ди­те при­мер трёхзнач­но­го на­ту­раль­но­го числа, ко­то­рое при де­ле­нии на 4 и на 15 даёт рав­ные не­ну­ле­вые остат­ки и пер­вая спра­ва цифра ко­то­ро­го яв­ля­ет­ся сред­ним ариф­ме­ти­че­ским двух дру­гих цифр. В от­ве­те ука­жи­те ровно одно такое число.

20.  В ма­га­зи­не бы­то­вой тех­ни­ки объём про­даж хо­ло­диль­ни­ков носит се­зон­ный ха­рак­тер. В ян­ва­ре было про­да­но 10 хо­ло­диль­ни­ков, и в три по­сле­ду­ю­щих ме­ся­ца про­да­ва­ли по 10 хо­ло­диль­ни­ков. С мая про­да­жи уве­ли­чи­ва­лись на 15 еди­ниц по срав­не­нию с преды­ду­щим ме­ся­цем. С сен­тяб­ря объём про­даж начал умень­шать­ся на 15 хо­ло­диль­ни­ков каж­дый месяц от­но­си­тель­но преды­ду­ще­го ме­ся­ца. Сколь­ко хо­ло­диль­ни­ков про­дал ма­га­зин за год?

13. . Бри­га­да ма­ля­ров кра­сит забор дли­ной 240 мет­ров, еже­днев­но уве­ли­чи­вая норму по­крас­ки на одно и то же число мет­ров. Из­вест­но, что за пер­вый и по­след­ний день в сумме бри­га­да по­кра­си­ла 60 мет­ров за­бо­ра. Опре­де­ли­те, сколь­ко дней бри­га­да ма­ля­ров кра­си­ла весь забор.

14.  Най­ди­те наи­мень­шее зна­че­ние функ­ции   на от­рез­ке  .

15.

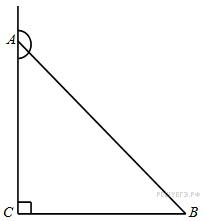
В тре­уголь­ни­ке   угол   равен 90°, синус внеш­не­го угла при вер­ши­не   равен 0,5,  . Най­ди­те  .

16. 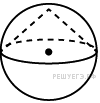  Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Ра­ди­ус сферы равен   Най­ди­те об­ра­зу­ю­щую ко­ну­са.

17.  Каж­до­му из четырёх не­ра­венств в левом столб­це со­от­вет­ству­ет одно из ре­ше­ний из пра­во­го столб­ца. Уста­но­ви­те со­от­вет­ствие между не­ра­вен­ства­ми и их ре­ше­ни­я­ми.

 

НЕ­РА­ВЕН­СТВА		РЕ­ШЕ­НИЯ
А)  Б)  В)  Г)		1)  2)  3)  4)

 

Впи­ши­те в при­ведённую в от­ве­те таб­ли­цу под каж­дой бук­вой со­от­вет­ству­ю­щую цифру. 

А	Б	В	Г

18.  Из­вест­но, что берёзы — де­ре­вья, также из­вест­но, что все де­ре­вья вы­де­ля­ют кис­ло­род. Под­сол­ну­хи тоже вы­де­ля­ют кис­ло­род. Вы­бе­ри­те утвер­жде­ния, ко­то­рые сле­ду­ют из при­ведённых дан­ных.

1) Все берёзы вы­де­ля­ют кис­ло­род

2) Все под­сол­ну­хи яв­ля­ют­ся берёзами

3) Не­ко­то­рые рас­те­ния, вы­де­ля­ю­щие кис­ло­род, яв­ля­ют­ся берёзами

4) Если рас­те­ние не вы­де­ля­ет кис­ло­род, то оно — не под­сол­нух

 

В от­ве­те ука­жи­те но­ме­ра вы­бран­ных утвер­жде­ний без про­бе­лов, за­пя­тых и дру­гих до­пол­ни­тель­ных сим­во­лов.

19.  При­ве­ди­те при­мер трёхзнач­но­го на­ту­раль­но­го числа, боль­ше­го 500, ко­то­рое при де­ле­нии на 3, на 4 и на 5 даёт в остат­ке 2 и в за­пи­си ко­то­ро­го есть толь­ко две раз­лич­ные цифры. В от­ве­те ука­жи­те ровно одно такое число.

20.  В бак объёмом 38 лит­ров каж­дый час, на­чи­ная с 12 часов, на­ли­ва­ют пол­ное ведро воды объёмом 8 лит­ров. Но в днище бака есть не­боль­шая щель, и из неё за час вы­те­ка­ет 3 литра. В какой мо­мент вре­ме­ни (в часах) бак будет за­пол­нен пол­но­стью.

Вариант № 8

1.  Най­ди­те зна­че­ние вы­ра­же­ния 

2.  Най­ди­те зна­че­ние вы­ра­же­ния  .

3. Тет­радь стоит 7 руб­лей. Сколь­ко руб­лей за­пла­тит по­ку­па­тель за 90 тет­ра­дей, если при по­куп­ке боль­ше 50 тет­ра­дей ма­га­зин де­ла­ет скид­ку 20% от сто­и­мо­сти всей по­куп­ки?

4.  Пло­щадь четырёхуголь­ни­ка можно вы­чис­лить по фор­му­ле   где  и   — длины диа­го­на­лей четырёхуголь­ни­ка,   — угол между диа­го­на­ля­ми. Поль­зу­ясь этой фор­му­лой, най­ди­те длину диа­го­на­ли   если     а  .

5.  Най­ди­те зна­че­ние вы­ра­же­ния  .

6.  Каж­дый день во время кон­фе­рен­ции рас­хо­ду­ет­ся 90 па­ке­ти­ков чая. Кон­фе­рен­ция длит­ся 3 дня. Чай продаётся в пач­ках по 50 па­ке­ти­ков. Сколь­ко пачек чая нужно ку­пить на все дни кон­фе­рен­ции?

7.  Най­ди­те ко­рень урав­не­ния  .

8.  Н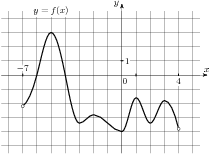 а ри­сун­ке изоб­ра­жен гра­фик функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те сумму точек экс­тре­му­ма функ­ции f(x).