3 Кінетостатичний аналіз

3.1 Визначення реакцій у кінематичних парах та зрівноважувальної сили методом кінетостатики

3.1.1. Для визначення реакцій у кінематичних парах механізму необхідно розподілити його на структурні групи і розглянути всі сили та моменти, що діють на ланки.

Згідно правил структурного аналізу даний механізм розподіляється на первинний механізм (тобто ведучу ланку) та одну структурну групу (групу Ассура), яка складається з ланок 2 та 3 (рис. 3.1).

а б

а – первинний механізм; б – структурна група

Рисунок 3.1 – Структурний розподіл кривошипно-шатунного механізму

3.1.2. Розглянемо спочатку структурну групу (рис. 3.1, б).

Покажемо всі сили та моменти, що діють на ланки 2 та 3, а також реакції, що виникають у кінематичних парах.

На ланки структурної групи діють: динамічний момент М_д2, сили ваги другої та третьої ланок та , сили інерції другої та третьої ланок та , сила опору , реакція опори на третю ланку , реакція дії першої ланки на другу з нормальною і тангенціальною складовими (рис. 3.2).

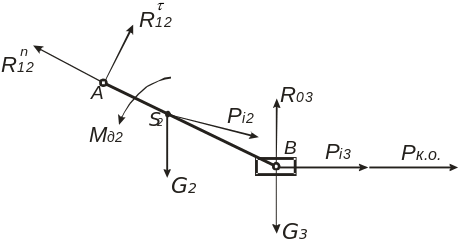
Рисунок 3.2 – Сили та реакції у кінематичних парах, що діють на структурну групу

При побудові необхідно дотримуватися наступних правил. Динамічний момент завжди направлений проти кутового прискорення . Сили інерції та завжди спрямовані у напрямку, протилежному до прискорень та відповідно, сила опору – у напрямку, протилежному до вектора швидкості точки В.

Реакція дії першої ланки на другу містить у собі дві складові: нормальну (спрямована вздовж осі ланки АВ у напрямку від точки В до точки А) і тангенціальну (спрямована у будь-який бік перпендикулярно до нормальної складової). Реакція дії опори (нерухомої ланки) на третю ланку проходить через точку В і спрямована вертикально (вгору або вниз).

3.1.3. Розрахуємо величини динамічного моменту, сил ваги та сил інерції.

, (3.1)

де – динамічний момент, Н∙м;

– момент інерції мас другої ланки відносно центру ваги, кг∙м²:

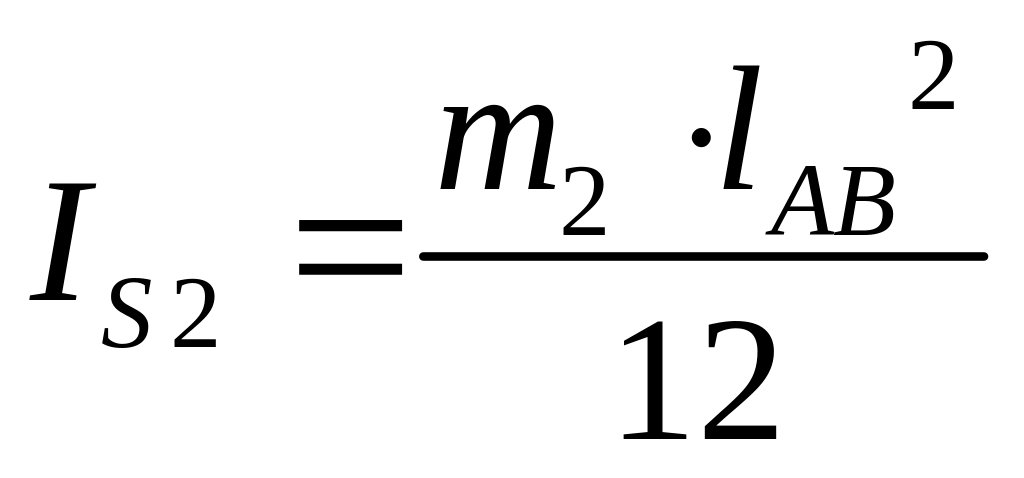. (3.2)

; (3.3)

, (3.4)

де m₂, m₃ – маси другої та третьої ланок відповідно, кг (з умови завдання);

l_AB – довжина ланки АВ, м (з умови завдання);

g – прискорення вільного падіння, g=9,8 м/с²;

G₂ і G₃ – сили ваги другої та третьої ланок відповідно, Н.

; (3.5)

, (3.6)

де , а_В – прискорення центру ваги другої ланки та прискорення повзуна відповідно, м/с²;

, – сили інерції другої та третьої ланок відповідно, Н.

3.1.4. Для знаходження сили опору необхідно побудувати діаграму навантаження (рис. 3.3). Діаграма має вигляд паралелограма і будується під планом механізму або над ним: крайній лівий кут паралелограма – під крайнім лівим положенням повзуна (на рис. 3.3 точка В₆), а крайній правий кут – під крайнім правим положенням повзуна (точка В₀). При цьому відстань ОS_max на діаграмі відповідає відстані В₀В₆ між двома крайніми положеннями повзуна механізму.

Мінімальне значення тиску р_min і максимальне його значення р_max та кут нахилу бічних сторін діаграми навантаження задаються викладачем.

Масштаб побудови μ_р діаграми визначається самостійно. Наприклад, для довільно вибраного h (див рис 3.3):

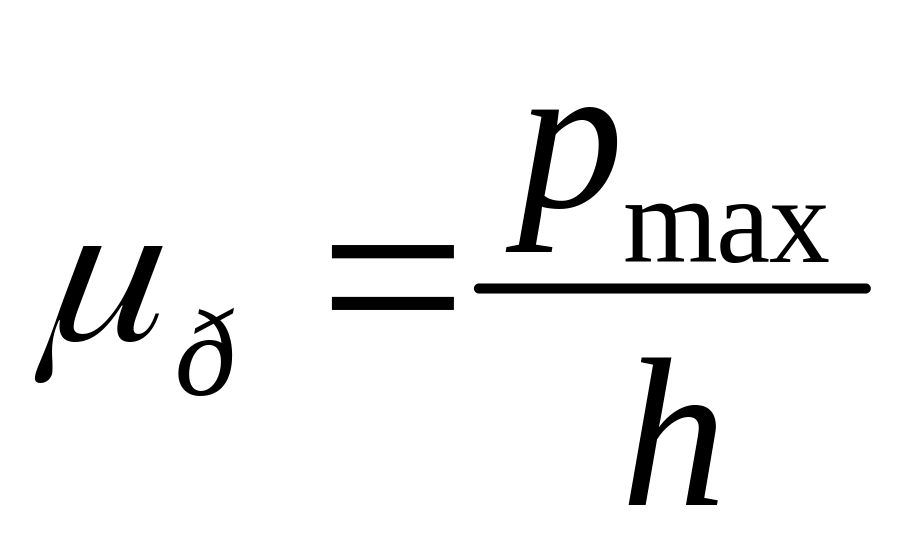, МПа/мм. (3.7)

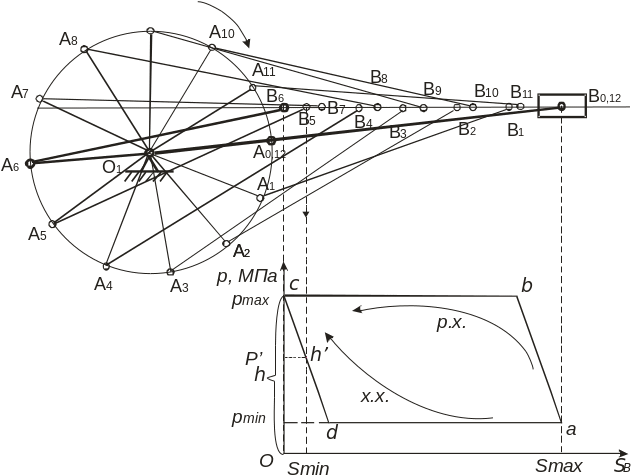
Рисунок 3.3 – Діаграма навантаження (залежність тиску на поршень р від переміщення повзуна S_B)

Щоб визначити силу опору для певного положення механізму (надалі – n-го положення), необхідно провести вертикальну пряму з точки В_n до перетину з паралелограмом. Причому слід враховувати, що робочому ходу відповідають більші значення тиску на діаграмі, а холостому – менші його значення. Так, на рисунку 3.3 ділянка аbc відповідає робочому ходу (р.х.), а ділянка adc – холостому ходу (х.х.).

3.1.5. Обчислимо силу опору:

, Н (3.8)

або

, Н, (3.9)

де р^/ – значення тиску у n-му положенні повзуна при певному h^/ (див. рис. 3.3):

, МПа; (3.10)

S_п – площа поршня:

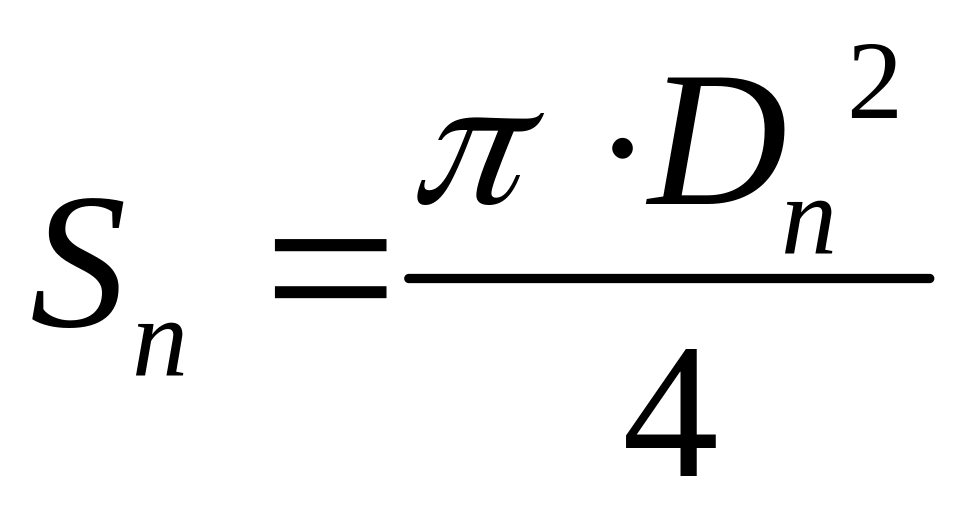, мм² (3.11)

де D_n – діаметр поршня, мм (з умови завдання).

3.1.6. Реакції , та визначаються з наступних умов рівноваги.

1. Сума моментів усіх сил відносно точки В дорівнює нулю:

; (3.12)

, (3.13)

де , та – плечі відповідних сил, мм (перпендикуляри з точки В до лінії дії сили, їх довжини вимірюються на листі).

З даного рівняння визначаємо тангенціальну складову реакції дії першої ланки на другу:

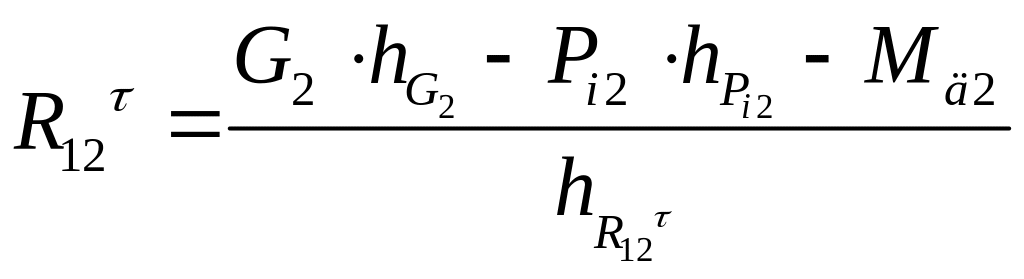, Н. (3.14)

Якщо результат одержали зі знаком «–», то напрямок дії реакції змінюється на протилежний.

2. Векторна сума всіх сил, що діють на ланки, дорівнює нулю:

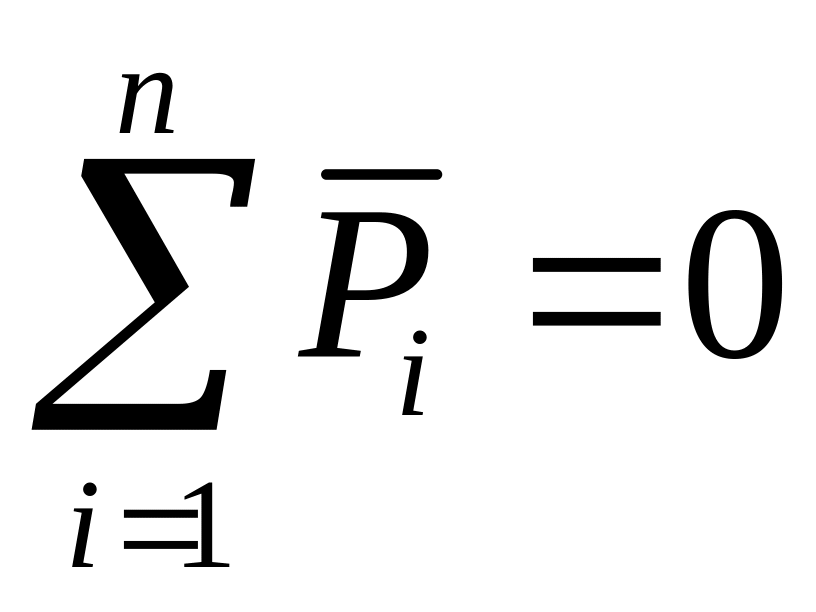; (3.15)

. (3.16)

За даним рівнянням рівноваги будуємо векторний силовий багатокутник. Невідомі реакції у рівнянні рівноваги слід записати на початку та в кінці виразу, а всі інші силові фактори - у довільному порядку.

3.1.7. Масштаб побудови багатокутника μ_р (Н/мм) визначається з огляду на найменшу за модулем силу з усіх, що входять до рівняння (3.16).

3.1.8. Побудуємо векторний силовий багатокутник. Для цього проводимо лінію, паралельну осі ланки АВ, вздовж якої діє реакція . Вибираємо на ній довільну точку і проводимо з неї вектор , що був визначений раніше. Далі, враховуючи масштаб μ_р, проводимо всі наступні вектори у порядку, вказаному в рівнянні рівноваги (3.16). Вектор реакції проводиться до перетину з лінією дії реакції . У результаті побудови одержимо довжини векторів та (рис. 3.4). Сумарний вектор реакції дії першої ланки на другу знайдемо як суму векторів та .

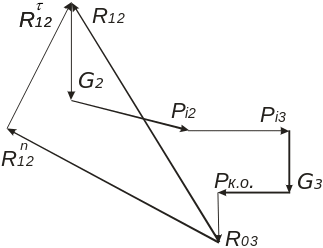
Рисунок 3.4 – Векторний силовий багатокутник

3.1.9. Визначимо числові значення знайдених реакцій:

, Н; (3.17)

, Н, (3.18)

де та – довжини векторів з багатокутника, мм;

μ_р - масштаб побудови багатокутника, Н/мм.

3.1.10. Сумарний вектор реакції дії першої ланки на другу:

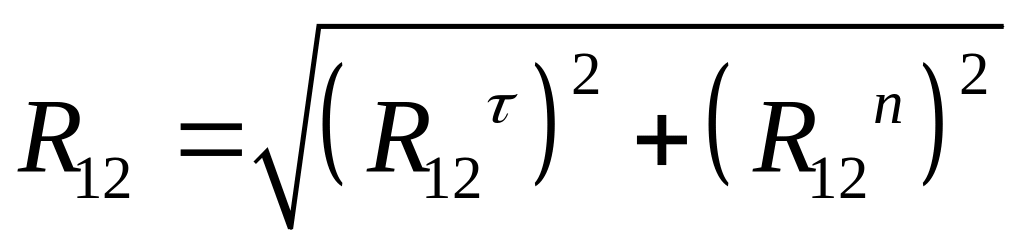, Н. (3.19)

3.1.11. Розглянемо первинний механізм. На нього діють: сила ваги першої ланки , реакція дії опори на першу ланку , реакція дії другої ланки на першу та зрівноважувальна сила (рис. 3.5).

Рисунок 3.5 – Схема сил, що діють на первинний механізм

Реакція опори на первинний механізм є невідомою і показується спочатку в довільному напрямку. Реакція дії другої ланки на першу показується у точці А протилежно до напрямку одержаної раніше реакції . Зрівноважувальна сила спрямована перпендикулярно до ланки О₁А (див. рис. 3.5).

3.1.12. Сила ваги першої ланки:

, Н. (3.20)

3.1.13. Реакцію та зрівноважувальну силу знаходимо з умов рівноваги.

1. Сума моментів усіх сил відносно точки О₁ дорівнює нулю:

; (3.21)

, (3.22)

де та – плечі зрівноважувальної сили та реакції дії другої ланки на першу відповідно, мм.

Звідси знаходимо зрівноважувальну силу:

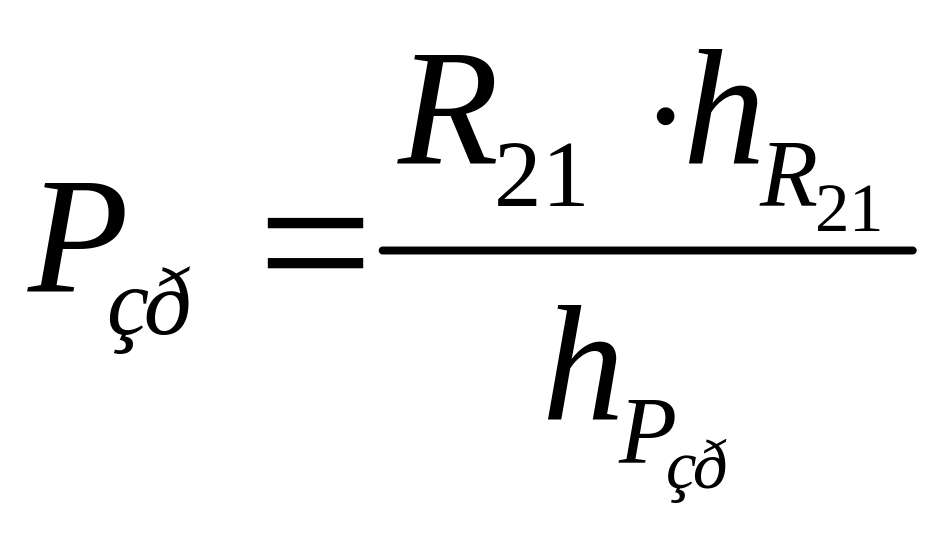, Н. (3.23)

Якщо одержали результат зі знаком «–», напрямок сили змінюємо на протилежний.

2. Векторна сума усіх сил, що діють на першу ланку, дорівнює нулю:

; (3.24)

. (3.25)

Для знаходження невідомої реакції згідно рівняння рівноваги будуємо векторний силовий багатокутник у вибраному масштабі. Масштаб побудови багатокутника μ_р визначаємо довільно за найменшою з сил, що входять до рівняння (3.25). Вектор реакції визначається як замикаючий в силовому багатокутнику (рис. 3.6).

Примітка. Масштаби побудови силових багатокутників при визначенні реакцій за рівняннями (3.16) та (3.25) можуть бути різними.

3.1.14. Величина реакції дії опори на першу ланку:

, (3.26)

де – довжина вектора реакції R₀₁ з багатокутника, мм;

μ_р – масштаб побудови, Н/мм.

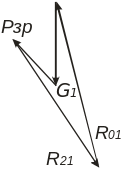
Рисунок 3.6 – Векторний багатокутник