31. Вещественная форма ряда Фурье.
Пусть функция f(x) удовлетворяет на [a; a+T] условиям Дирихле, тогда она представима на этом промежутке рядом Фурье:
f(x)
=
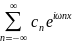(1) , где Cn
=
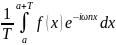(2)
Преобразуем ряд (1)
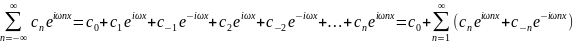
Используя формулы:
eiy=cosy + isiny; e-iy= cosy – isiny, получим:
f(x) =
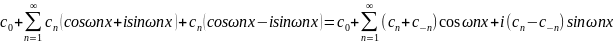
Ввведем обозначения:
c0=a0/2 ; cn+c-n=an ; i(cn-c-n) = bn
Имеем
f(x)=
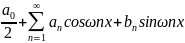
Получим формулы для коэффициентов
a0=
2c0 =
;
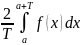an =
cn+
c-n =
так как cosy=
,
то an=
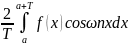
bn
= i(cn
– c-n)
= i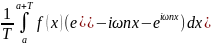
так как sinsy=
,
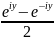то bn=
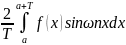
Итак, ряд Фурье в вещественной форме для функции f(x) на [a; a+T] имеет вид:
f(x) =
a0 =
an=
bn=
Достаточные условия разложимости функции в ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.
Фотки
Разложение функции в ряд Фурье на отрезке произвольной длины. Фотки
Ряд Фурье в комплексной форме. Фотки
Интеграл Фурье как предельный случай ряда Фурье. Вещественная форма интеграла Фурье
Непериодическая функция f(x) не может быть разложена в ряд Фурье, однако если функция удовлетворяет условиям Дирихле, то она может быть представлена интегралом Фурье.
При этом функция
f(x) должна
быть еще и абсолютно интегрируемой, то
есть
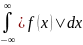должен быть конечным. Тогда для всех x
имеет место равенство:
f(x)=
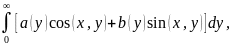(1)
, где
a(y) =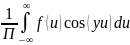
b(y) =
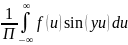
Правая часть (1) есть интеграл Фурье функции f(x).
Если f-
четная, то b(y)=0,
a(y) =
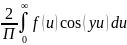
F(x) =
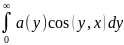
Если f-
нечетная, то a(y)
=0, b(y)=
f(x)=
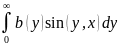
Интеграл Фурье в комплексной форме. Прямое и обратное преобразование ряда.-
Изображение функции по Лапласу. Простейшие свойства преобразования Лапласа.
Пусть задана функция
действительной переменной t,
определенная при t
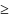0.
Будем считать, что функция f(t) кусочно- непрерывная, т.е. такая, что в любом конечном интервале она имеет конечное число точек разрыва первого рода.
Будем предполагать, что существуют постоянные положительные числа М и S0 такие, что
|f(t)|<
M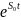
(1)
Рассмотрим произведение функции f(t) на комплексную функцию e-pt, где p = a+ib (a>0):
e-ptf(t)e-ibt = e-atf(t)cosbt-ie-atf(t)sinbt
Рассмотрим несобственный интеграл:
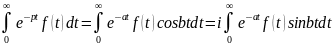
Покажем, что если функция f(t) удовлетворяет условию (1) и a>S0, то интегралы , стоящие в правой части равенства, существуют, и сходимость интегралов абсолютная.
Оценим первый:
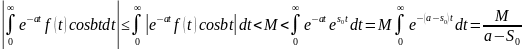
Аналогично оцениваем
второй интеграл. Итак, интеграл
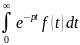существует. Он определяет некоторую
функцию от р ,
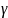мы обозначим F(p)
F(p) =
Функция F(p) называется Лапласовым изображением или L-изображением, или просто изображением функции f(t).
Функцию f(t) называют начальной функцией (оригиналом)
Если F(p)
есть изображение функции f(t),
то
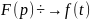
Из определения изображения следуют его простейшие свойства:
Линейность
Для любых комплексных постоянных a и b
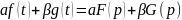
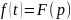g(t)
= G(p)
Теорема подобия
Для любого постоянного а>0
f(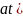
=1/2F(p/2)
Дифференцирование оригинала
Если функции f(t),
f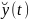
,
f|(t)…fn(t)
является функциями- оригиналами и
f(t)=F(p)
, то f’(t) =
pF(p) – f(0)
f’’(t) = p2F(p)-pf(0)-f’(0)
fn(t)
= pnF(p)
– pn-1f(0)
– pn-2f’(0)-…fn-1(0),
где под fk(0)
(k=1,2…3) понимается
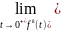
Дифференцирование изображения
Дифференцирование изображения сводится к умножению на (t) оригинала
F’(p) = -tf(t) или Fn(p) = (-t)nf(t)
Интегрирование оригинала
Интегрирование
оригинала сводится к делению изображения
на p , т.е. если f(t)
= F(p), то
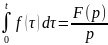
Интегрирование изображения
Если интеграл
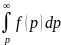сходится,
то он служит изображением функции
Теорема смещения
Если f(t)
= F(p) , то для
любого комплексного !!!
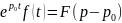
Теорема запаздывания
Если f(t) = F(p) , то для любого t>0
F(t-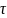
)
=
Теоремы подобия, смещения и запаздывания операции исчисления.
Теорема подобия
Для любого постоянного а>0
f( =1/2F(p/2)
Теорема смещения
Если f(t) = F(p) , то для любого комплексного p0
Теорема запаздывания
Если f(t) = F(p) , то для любого t>0
F(t- ) =
Дифференцирование и интегрирование оригинала и изображения функции.
Дифференцирование оригинала
Если функции f(t), f , f|(t)…fn(t) является функциями- оригиналами и f(t)=F(p) , то f’(t) = pF(p) – f(0)
f’’(t) = p2F(p)-pf(0)-f’(0)
fn(t) = pnF(p) – pn-1f(0) – pn-2f’(0)-…fn-1(0), где под fk(0) (k=1,2…3) понимается
Дифференцирование изображения
Дифференцирование изображения сводится к умножению на (t) оригинала
F’(p) = -tf(t) или Fn(p) = (-t)nf(t)
Интегрирование оригинала
Интегрирование оригинала сводится к делению изображения на p , т.е. если f(t) = F(p), то
Интегрирование изображения
Если интеграл сходится, то он служит изображением функции