26. Ряды с функциональными членами; точка сходимости и область сходимости.

Последовательность функций U₁(x),U₂(x),…U_n(x) от одной и той же переменной х, определенных на некотором числовом множестве Х , называется функциональной последовательностью.

Если для любого значения x принадлежащего X, существует конечный предел 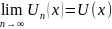, то говорят , что на множестве Х определена предельная функция для функциональной последовательности.

Функциональным рядом называется выражение вида U₁(x) + U₂(x) +…+ U_n(x) +… =

Точка x_{0 ­­}принадлежащая Х, такая , что числовой ряд U₁(x₀) + U₂(x₀) + …+ U_n(x₀) +… = сходится , называется точкой сходимости ряда. Множество всех точек сходимости ряда называются областью сходимости ряда.

27. Понятие степенного ряда. Теорема Абеля. Интервал сходимости.

Степенным рядом называется функциональный ряд вида a₀+ a₁x +a₂x² +…a_nxⁿ =

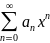
a₀,a₁,a₂…a_n­ – постоянные числа, называемые коэффициентами степенного ряда.

Теорема Абеля:

Если степенной ряд сходится при x=x₀ (x₀ не равно 0), то он сходится абсолютно при всех х, удовлетворяющих неравенству |x|<|x₀|

Следствие из теоремы Абеля:

Если ряд 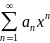сходится не при всех значениях х, то существует такое число R>0 , что :

1. Ряд сходится абсолютно при всех х, удовлетворяющих неравенству |x|<R

2. Ряд сходится при всех х, удовлетворяющих неравенству |x|>R

3. Число R называют радиусом сходимости степенного ряда, а интервал (R,-R) – интервалом сходимости степенного ряда.

Замечание 1: Любой степенной ряд имеет свой радиус сходимости

Замечание 2: Существуют степенные ряды, у которых радиус сходимости R=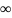 , а также ряды R = 0

Замечание 3: При x=R и x=-R степенной ряд может как сходиться, так и расходиться.

Теорема:

Пусть дан ряд . Тогда, если существует предел 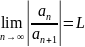, то радиус сходимости данного ряда совпадает с этим пределом, т.е. R=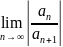

28. Ряд Тейлора.

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

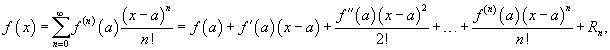
где R_n − остаточный член в форме Лагранжа определяется выражением

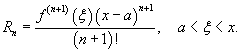
Если приведенное разложение сходится в некотором интервале x, т.е. , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена:

29. Разложение элементарных функций в ряд Маклорена. Применение степенных рядов в приближенных значениях.

Если a = 0, то такое разложение называется рядом Маклорена: (из пред. вопроса)

Применение степенных рядов в приближенном вычислении:

Например, требуется найти sin1 с точностью до 0.001



Находим sin 1 = 1 – 1/3! + 1/5! – 1/7! + 1/9!...

1/5! = 0.0083>0.001

1/7! = 0.0002<0.001

Sin1= 1-1/3!+1/5!=0,842; Табличное значение sin 1 =0.8415

30. Тригонометрическая система функций. Коэффициенты Фурье функции. Формулы Фурье.

Система функций 1,cosx,sinx,cos2x,sin2x…cosnx,sinnx… называется тригонометрической системой.

Ряд вида

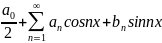(1) называется тригонометрическим рядом, а числа a_n,b_n, n=1.2…- его коэффициентами. n-частота.

Тригонометрическая система функций (1) имеет следующие свойства:

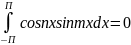
1. Интеграл по отрезку [-П,П] от произведения двух различных функций этой системы равен -, т.е. 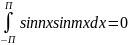, где n не равен 0.

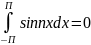
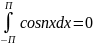(n=1,2…)

2. Интеграл по отрезку [-П,П] от функций sin²nx,cos²nx ( n=1,2) равен П, т.е.

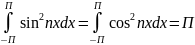
Теорема: Пусть на промежутке [-П,П] ряд (1) сходится равномерно и f(x) – их сумма, f(x) = , x принадлежит [-П,П]

Тогда

a_n= 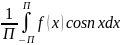(2)

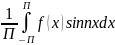b_n= (3)

Пусть функция f(x) абсолютно интегрируема на отрезке [-П,П]. Тогда тригонометрический ряд (1), коэффициенты задаются уравнениями (2) и (3) называется рядом Фурье функции f(x) на промежутке [-П,П], а числа a₀,a_n,b_n n принадлежит N – коэффициентами Фурье этой функции