12. Линейное неоднородное дифференциальное уравнение со специальной правой частью; нахождение его частного решения когда правая часть равна

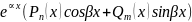
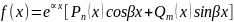
Частное решение в этом случае:

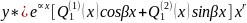
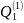- многочлены, степень которых равна наивысшей степени многочленов P_n(x)  и Q_m(x) , т.е. e=max(m,n);

r- число корней хар-кого уравнения, равных значению

Например, y” – 5y’ +6y = 13sin3x

k²-5k+6 =0

D = 25-24 = 1

k₁=3; k₂=2

= С₁e^3x + C₂e^2x

y*= Asin3x + Bcos3x

y*’=3Acos3x – 3Bsin3x

y*” = -9Asin3x – 9Bcos3x

-9Asin3x – 9Bcos3x – 5(3Acos3x -3Bsin3x) + 6(Asin3x+Bcos3x) = 13sin3x

-9sin3x -9Bcos3x -15Acos3x +15Bsin3x + 6Asin3x +6Bcos3x = 13sin3x

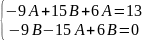
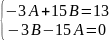B= -15A/3 = -5A

-3A +15(-5A) = 13

-3A – 75A = 13

-78A = 13; A= -13/78; B= 65/78

y*= -13/78 sin3x + 65/78 cos3x

y= + y*= C₁e^3x +C₂e^2x –13/78 sin3x + 65/78 cos3x

12. Нормальная система дифференциальных уравнений 1-го порядка; структура общего решения системы линейных однородных уравнений 1-го порядка ; интегрирование системы дифференциальных уравнений методом исключений

Фотки

20. Понятие числового ряда ; частичная сумма ряда

Пусть каждому натуральному числу n поставлено в соответствие по определенному признаку (правилу) a_n­, тогда совокупность чисел a_n- числовая последовательность.

Формальная запись бесконечной суммы чисел a₁+a₂+…a_n – числовой ряд, а числа a­₁,a_2…,a_n-члены ряда

Сумма конечного числа n первых членов ряда называется n-ной частичной суммой рядов

S_n=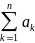

Ряд, членами которого являются все члены исходного ряда, начиная с (n+1) называются

n-ным остатком исходного ряда r_n = a_n+1+a_n+2 +…

21. Сходимость числового ряда; необходимое условие сходимости ряда, критерий Коши сходимости ряда.

Сходимость числового ряда. Ряд    называют сходящимся, если существует и конечен предел последовательности     частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают  , 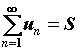. Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность называется остатком ряда. Очевидно, что для сходящегося ряда   . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то  (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.

Необходимое условие сходимости ряда:

Если ряд -сходится, то его общий член стремится к нулю:

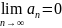
Критерий Коши сходимости ряда:

Для того, чтобы ряд 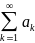сходился, необходимо и достаточно, чтобы

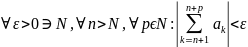
21. Числовой ряд с положительными членами. Признаки сравнения сходимости ряда с положительными членами.

Числовой ряд называется знакоположительным, если все его члены положительны, то есть, .

Необходимое и достаточное условие сходимости знакоположительного числового ряда.

Для сходимости знакоположительного числового ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Начнем с признаков сравнения рядов. Их суть заключается в сравнении исследуемого числового ряда с рядом, сходимость или расходимость которого известна.

Первый, второй и третий признаки сравнения.

Первый признак сравнения рядов.

Пусть и - два знакоположительных числовых ряда и выполняется неравенство для всех k = 1, 2, 3, ... Тогда из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .

Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом , то есть, гармонический ряд.

Второй признак сравнения.

Пусть и - знакоположительные числовые ряды. Если , то из сходимости ряда следует сходимость . Если , то из расходимости числового ряда следует расходимость .

Следствие.

Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.

Исследуем ряд на сходимость с помощью второго признака сравнения. В качестве ряда возьмем сходящийся ряд . Найдем предел отношения k-ых членов числовых рядов:

Таким образом, по второму признаку сравнения из сходимости числового ряда следует сходимость исходного ряда.

Признак Коши. Пусть для числового ряда ( 1 ) с положительными членами существует предел

                                        σ =

Тогда при σ < 1 ряд сходится, а при σ > 1 ряд расходится.

Можно указать как сходящиеся, так и расходящиеся ряды, для которых σ = 1.