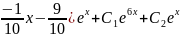8. Линейные дифференциальные уравнения n-го порядка, структура общего решения

Дифференциальное уравнение n-го порядка символически можно записать в виде:

F(x,y,y’,y’’,…,yⁿ)=0

Дифференциальное уравнение n-го порядка называется линейным, если оно первой степени относительно совокупности искомой функции y и её производных y’,…, y^n-1,yⁿ т.е. a₀yⁿ + a₁y^(n-1) + …a_ny = f(x)

f(x)-правая часть уравнения

Если f(x)=0 – ур-е однородное, если не равно 0 – ур-е неоднородное

Теорема 1: Если y₁ и y₂ – 2 частных решения линейного уравнения второго порядка, то y₁+y₂ – тоже решение этого уравнения.

Теорема 2: Если y₁- решение уравнения, C- постоянная, то Cy₁ решение уравнения.

Два решения уравнения (y₁ и y₂) являются линейно зависимыми на отрезке [a,b] если y₁/y₂=const, иначе линейно независимы

Если y₁ и y₂ суть функции от x, то определитель

W(y₁,y₂)=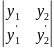 = y₁y₂’-y₁’y₂- определитель Вронского данных функций)

W(y₁,y₂)=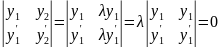

Теорема 3: Если определитель Вронского W(y₁,y₂), составленный для решений y₁ и y₂ линейного однородного уравнения, не равен нулю при каком-нибудь значении x=x₀ на отрезке [a,b], где коэффициенты уравнения непрерывны, то он не обращается в 0 ни при каком значении x на этом отрезке.

Теорема 4: Если решения y₁ и y₂ уравнения линейно независимы на отрезке [a,b], то определитель Вронского W, составленный для этих решений , не обращаются в нуль ни в одной точке указанного отрезка

Теорема 5: Если y₁ и y₂ – два линейно независимых решения уравнения, то y=C₁y₁+C₂y₂

Теорема 6: Если известно одно частное решение линейного однородного уравнения второго порядка, то нахождение общего решения сводится к интегрированию функций.

9. Решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами.

y’’+py’+qy=0 – общий вид уравнения

Записываем характеристическое уравнение:

k²+pk+q=0

1.p²/4-q > 0 k₁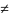 k₂ -вещественные

у=С₁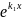 + С₂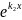

2. p²/4-q < 0 k₁ k₂ - комплексные

;

;

,

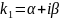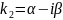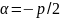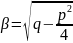
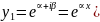+i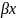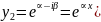*sin )

-i*sin )

3. p²/4-q = 0 k₁=k₂=k

y₁=

Общий интеграл у=С₁ + С₂ =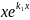

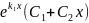
10. Структура решения линейного неоднородного дифференциального уравнения n-го порядка.

y”+a₁y’+a₂y=f(x)

Теорема 1: Общее решение неоднородного уравнения представляется как сумма какого-нибудь частного решения этого уравнения y* и общего решения соответствующего однородного уравнения

y=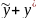 -общее решение

Теорема 2: Решение y* уравнения y”+a₁y’+a₂y=f₁(x)+f₂(x), где правая часть есть сумма двух функций f₁(x) и f₂(x), то y*=y₁*+y₂*, где y₁* и y₂* есть соответственно решение уравнений

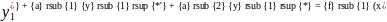
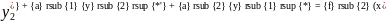
11. Определение частного решения линейного неоднородного дифференциального уравнения 2-го порядка методом вариации произвольных постоянных.

Метод вариации постоянных

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения. Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений  y₁(x) и y₂(x):

12. 

где C₁, C₂ − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C₁ и C₂ рассматриваются функции C₁(x) и C₂(x), которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению. Производные неизвестных функций C₁(x) и C₂(x) можно определить из системы уравнений

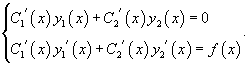
Главным определителем этой системы является вронскиан функций y₁ и y₂, который не равен нулю в силу линейной независимости решений y₁ и y₂. Поэтому данная система уравнений всегда имеет однозначное решение. Окончательные формулы для C₁' (x) и C₂' (x) имеют вид

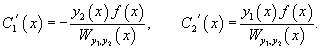
Применяя метод вариации параметров, важно помнить, что функция f(x) должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент a₀(x) перед старшей производной должен быть равен 1. Далее, зная производные C₁' (x) и C₂' (x), можно найти и сами функции C₁(x) и C₂(x):

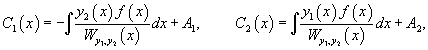
где A₁, A₂ − постоянные интегрирования. Тогда общее решение исходного неоднородного уравнения будет выражаться формулой

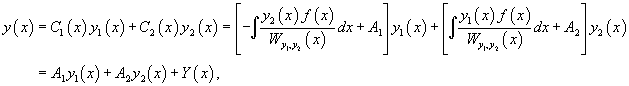
в которой

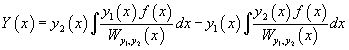
обозначает частное решение неоднородного уравнения.

Пример

Найти общее решение дифференциального уравнения  x²y'' − 2xy' + 2y = x² + 1 (при x > 0).

Решение.

Рассмотрим сначала однородное уравнение и построим его фундаментальную систему решений. Можно заметить, что одним из решений однородного уравнения

     

является функция y₁ = x. Найдем второе независимое решение y₂ по формуле Лиувилля-Остроградского:

     

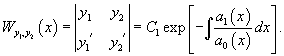
Следовательно,

     

Делим обе части уравнения на y₁²:

     

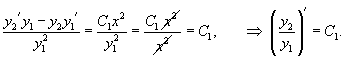
После интегрирования имеем

     

Итак, общее решение однородного уравнения выражается функцией

     

где C₁, C₂ − произвольные постоянные. Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C₁ и C₂ как функции от переменной x. Производные этих функций определяются из системы уравнений

     

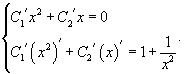
Здесь правая часть во втором уравнении записана после преобразования исходного дифференциального уравнения в стандартную форму:

     

Решая данную систему уравнений, находим производные C₁' (x), C₂' (x) и затем сами функции C₁(x) и C₂(x). Имеем

     

где A₁, A₂ − постоянные интегрирования. В результате получаем общее решение неоднородного уравнения в виде

     

12. Линейное неоднородное дифференциальное уравнение со специальной правой частью; нахождение его частного решения когда правая часть равна 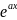*P_n(x)

f(x) = *P_n(x)

Частное решение следует искать в виде: y*=x^rQ_n(x) , где Q_n(x) - многочлен такой же степени как и P_n(x); r- число корней характеристического уравнения k²+pk+q=0, совпадающих с

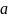
Например, y” – 7y’ + 6y = (x-2)e^x

y*= xQ₁(x)e^x = x(Ax+B)e^x

1. Решим однородное уравнение

k²-7k+6=0

D= 49 – 4*6 = 25 = 5²>0

k₁= 6; k₂ = 1.

Следовательно общее решение однородного уравнения :

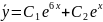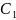, где и 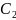– постоянные числа.

Так как k₂=1 совпадает с e^1x, то частное решение неординарного уравнения будем искать в виде y₂= x(Ax+B)e^x

y₂’= (Ax²+Bx)e^x = (2Ax+B)e^x + (Ax²+Bx)e^x

y₂”= 2Ae^x + (2Ax+B)e^x + (2Ax+B)e^x + (Ax²+Bx)e^x

Подставляем:

2Ae^x +(2Ax+B)e^x + (2Ax+B)e^x + (Ax²+Bx)e^x – 7((2Ax+B)e^x) + (Ax²+Bx)e^x) + 6xe^x (Ax+B)= (x-2)e^x

2A + 2Ax + B + 2Ax + B + Ax² + Bx – 14 Ax – 7B – 7 Ax² – 7Bx +6x(Ax+B)= xe^x

2A + 10Ax + 2B - 6Ax² – 6Bx + 6Ax² + 6xB = x-2

2A + 2B – 10Ax = x-2

-10Ax +(2A +2B) = x-2

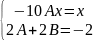
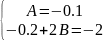
2B = -2+0.2 = -9/5

B= -9/5*1/2 = -9/10

y* = x (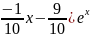

y=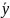 + y*=x (