Линейные дифференциальные уравнения первого порядка
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
Использование интегрирующего множителя;
Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение диффференциального уравнения выражается в виде:
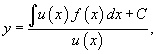
где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Уравнение Бернулли
Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде
где a(x) и b(x) − непрерывные функции. Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки
Новое дифференциальное уравнение для функции z(x) имеет вид
Найти общее решение уравнения y' − y = y2ex.
Решение.
Для заданного уравнения Бернулли m = 2, поэтому сделаем подстановку
Дифференцируя обе части уравнения (переменная y при этом рассматривается как сложная функция x), можно записать:
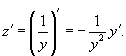
Разделим обе части исходного дифференциального уравнения на y2:
Подставляя z и z', находим:
Мы получили линейное уравнение для функции z(x). Решим его с помощью интегрирующего множителя:
Общее решение линейного уравнения выражается формулой
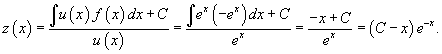
Возвращаясь к функции y(x), получаем ответ в неявной форме:
который можно записать также в виде:
Заметим, что при делении уравнения на y2 мы потеряли решение y = 0. В результате, полный ответ записывается в виде:
Дифференциальные уравнения в полных дифференциалах
Дифференциальное уравнение вида
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
Общее решение уравнения в полных дифференциалах определяется формулой
где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
Алгоритм решения уравнения в полных дифференциалах
Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
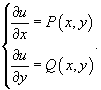
Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
Отсюда получаем выражение для производной неизвестной функции φ(y):
Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
Общее решение уравнения в полных дифференциалах записывается в виде:
