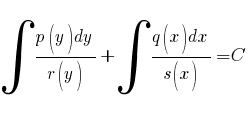1. Понятие дифференциального уравнения (ду). Общее и частное решение ду. Задача Коши для ду 1-го порядка.

Дифференциальные уравнения – это соотношение вида F(x₁,x₂,x₃,..,y,y′,y′′,...y⁽ⁿ⁾) = 0, связывающее независимые переменные x₁,x₂,x₃,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов.

Обыкновенные дифференциальные уравнения – это дифференциальные уравнения, в которых содержится только одна независимая переменная.

Дифференциальные уравнения в частных производных – это дифференциальные уравнения, в которых содержится две и более независимых переменных.

Решение дифференциального уравнения – это функция y(x), определенная и достаточное число раз дифференцируемая в некоторой области, при подстановке которой в исходное уравнение получается тождество.

Общее решение дифференциального уравнения – это соотношение вида y = y(x,C₁,C_2,C₃,...C_n), зависящее от n произвольных постоянных.

Частное решение дифференциального уравнения – это общее решение при заданных значениях постоянных C₁,C_2,C₃,...C_n.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

2. Дифференциальные уравнения с разделяющимися переменными.

Дифференциальные уравнения с разделяющимися переменными – это уравнения вида

В исходном уравнении:

Выразим y' через дифференциалы: ; ; Умножим на dx: ;

Иногда уравнение задается в таком виде. Это означает, что переменные x и y равноправны. Разделим уравнение на s(x)r(y): Интегрируем:

3. Однородные дифференциальные уравнения

Однородные дифференциальные уравнения первого порядка – это уравнения вида

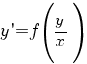
Как распознать однородное дифференциальное уравнение

Для того, чтобы распознать однородное дифференциальное уравнение, нужно ввести постоянную t и сделать замену y → ty, x → tx. Если, в результате такого преобразования, постоянная t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется:

Пример 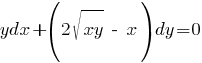Делаем замену y → ty, x → tx: , или . Сокращаем на t²:

Уравнение не содержит t - значит это однородное уравнение.

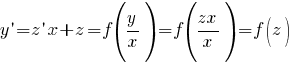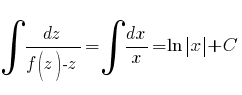Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки: y = zx, где z - функция от x. Действительно, y′ = (zx)′ = z′x + z(x)′ = z′x + z Подставляем в исходное уравнение: , или , или Разделяем переменные. Умножим на dx и разделим на x(f(z) - z). При f(z) - z ≠ 0 и x ≠ 0 получаем: Интегрируем: И мы получили общий интеграл уравнения: Постоянную интегрирования C часто бывает удобно записать в виде lnC, тогда Знак модуля можно опустить, поскольку нужный знак определяется выбором знака постоянной C. Тогда общий интеграл примет вид:

Далее следует рассмотреть корни уравнения: f(z) - z = 0 и решение x = 0 (если есть смысл).