34. Ряд Фурье в комплексной форме

Определение 1. Функциональный ряд вида

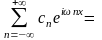
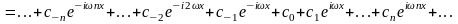(1)

называется тригонометрическим рядом. Числа 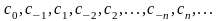называются коэффициентами ряда.

Определение 2. Тригонометрический ряд называется рядом Фурье для функции на , если коэффициенты ряда вычисляются по формулам

. (2)

Теорема (Необходимый признак представительности функции тригонометрическим рядом)

Для того, чтобы функция была представима на тригонометрическим рядом вида 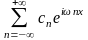, необходимо, чтобы этот ряд являлся рядом Фурье, т.е. чтобы коэффициенты 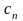вычислялись по формулам , .

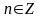Доказательство

Пусть функция представима на тригонометрическим рядом .

Умножим обе части этого равенства на :

.

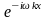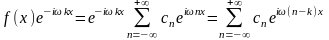Предполагая возможность интегрирования под знаком ряда, проинтегрируем по промежутку :

.

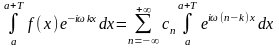Т.к.

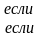
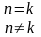, то

.

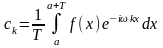3 5. Интеграл Фурье как предельный случай ряда Фурье; вещественная форма интеграла Фурье

36. Интеграл Фурье в комплексной форме. Прямое и обратное преобразование Фурье.

37. Изображение функции по Лапласу. Простейшие свойства преобразования Лапаласа

Функцией-оригиналом называется комплекснозначная функция f (t) действительного аргумента t, удовлетворяющая условиям:

1. f (t) интегрируема на любом конечном интервале оси t;

2. f (t)=0 для всех отрицательных t;

3.  f (t) возрастает не быстрее показательной функции, т. е. существуют такие постоянные М и 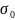 , что 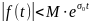 для всех t

Изображением функции  f (t) (по Лапласу) называется функция F(p) комплексного переменного p= +i , определяемая равенством

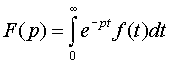
Тот факт, что F(p) есть изображение  f (t), будем символически записывать так:

Для любой функции-оригинала  f (t) изображение определено в полуплоскости Rep>₀ и является в этой полуплоскости аналитической функцией.

Из определения изображения следуют его простейшие свойства:

Линейность. Для любых комплексных постоянных a и b:

f(t)=F(p), g(t)=G(p)

Теорема подобия. Для любого постоянного a >0

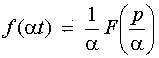
Дифференцирование оригинала. Если функции f (t), f (t) , f (t),…, f ⁽ⁿ⁾(t) являются функциями-оригиналами и f(t)=F(p), то

,

,

,

где под f ^(k)(0), (k= 1, 2,…, n-1) понимается 

4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала

или вообще

.

5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то

.

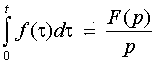6. Интегрирование изображения. Если интеграл  сходится, то он служит изображением функции

.

7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р₀

.

8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0

.

38. Теоремы подобия, смещения и запаздывания операционного исчисления

Операционное исчисление в настоящее время стало одной из важнейших глав практического математического анализа. Операционный метод непосредственно используется при решении обыкновенных дифференциальных уравнений и систем таких уравнений; его можно использовать и при решении дифференциальных уравнений в частных производных.

 Преобразование Лапласа 

(f - оригинал; F - изображение).

     Запись 

     Условия на оригинал 

     1. 

     2. f - кусочно-непрерывна на R.

     3.   такие, что 

     Линейность 

     Теорема подобия 

     Если   то 

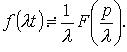
     Теорема запаздывания 

     Если   то 

     Теорема смещения 

     Если   то