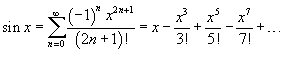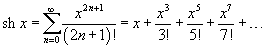- •Уравнение с разделяющимеся переменными
- •Однородные дифуравнения
- •Линейное уравнение первого порядка
- •Уравнение Бернулли.
- •Определение уравнения в полных дифференциалах
- •Дифуравнения второго порядка
- •Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами
- •Структура решения линейного неоднородного уравнения
- •Вопрос 11. Определение частного решения линейного неоднородного диф. Уравнения 2-го порядка методом вариации произвольных постоянных(метод Лагранжа).
- •Вопрос 12.
- •Вопрос 13. Линейное неоднородное дифференциальное уравнение со специальной правой частью; нахождение его частного решения, когда правая часть равна
- •Вопрос 14. Нормальная система диф. Уравнений 1-го порядка; структура общего решения системы линейных однородных диф. Уравнений 1-го порядка.
- •Вопрос 15.Решение системы диф. Уравнений 1-го порядка методом вариации произвольных постоянных.
- •Вопрос 16
- •17. Квазилинейные дифференциальные уравнения в частных производных первого порядка; характеристики квазилинейного дифференциального уравнения.
- •Вопрос 18.Решение квазилинейного диф. Уравнения в частных производных 1-го порядка.
- •Вопрос 19
- •Вопрос 20. Понятие числового ряда
- •21.Сходимость числового ряда
- •22.Числовой ряд с положительными членами.
- •23.Признак Даламбера сходимости ряда
- •24. Знакопеременные ряды
- •25. Знакочередующиеся ряды
- •Вопрос 26. Ряды с функциональными числами. Точка сходимости и область сходимости
- •Вопрос 27.Понятие степенного ряда. Теорема Абеля. Интервал сходимости.
- •1. Основные понятия. Область сходимости.
- •28. Ряд Тейлора
- •29. Разложение элементарных функций в ряд Маклорена. Применение степенных рядов в приближенных вычислениях
- •30. Тригонометрическая система функций. Коэффициенты Фурье функции, формулы Фурье Тригонометрическая система
- •31. Вещественная форма ряда Фурье
- •32. Достаточное условия разложимости функции в ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.
- •33. Разложение функции в ряд Фурье на отрезке произвольной длины
- •34. Ряд Фурье в комплексной форме
- •3 5. Интеграл Фурье как предельный случай ряда Фурье; вещественная форма интеграла Фурье
- •36. Интеграл Фурье в комплексной форме. Прямое и обратное преобразование Фурье.
- •37. Изображение функции по Лапласу. Простейшие свойства преобразования Лапаласа
- •38. Теоремы подобия, смещения и запаздывания операционного исчисления
- •39. Дифференцирование и интегрирование оригинала и изображения функции
- •40. Решение линейных дифференциальных уравнений с постоянными коэффициентами с помощью операционного исчисления
Вопрос 27.Понятие степенного ряда. Теорема Абеля. Интервал сходимости.
1. Основные понятия. Область сходимости.
Определение 1.1. Степенным рядом называется функциональный ряд вида
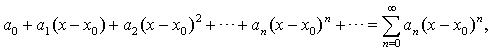 (1.1)
(1.1)
где a0, a1, a2, …,an,…, а также x0 – постоянные числа. Точку x0 называют центром степенного ряда.
Сначала рассмотрим степенные ряды с центром 0, т.е. ряды вида
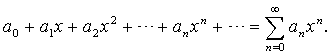 (1.2)
(1.2)
Такой ряд всегда сходится при x=0 и, значит, его область сходимости есть непустое множество.
Теорема
1.1. (теорема Абеля). Если
степенной ряд (1.2) сходится при некотором ![]() ,
где
,
где![]() -число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что
-число,
не равное нулю, то он сходится абсолютно
при всех значениях x таких,
что ![]() Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что
Наоборот,
если ряд (12) расходится при
,
то он расходится при всех значениях x таких,
что ![]()
Доказательство. Пусть числовой ряд
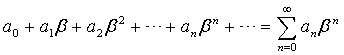 (1.3)
(1.3)
сходится.
Поэтому ![]() Но
любая последовательность, имеющая
предел, ограничена, значит, существует
такое число M,
что
Но
любая последовательность, имеющая
предел, ограничена, значит, существует
такое число M,
что ![]() для
всех n=0,1,2,…
для
всех n=0,1,2,…
Рассмотрим теперь ряд
![]() (1.4)
(1.4)
предполагая,
что ![]() Так
как
Так
как 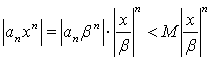 и
при этом
и
при этом ![]() то
члены ряда (3.4) не превосходят соответствующих
членов сходящегося ряда
то
члены ряда (3.4) не превосходят соответствующих
членов сходящегося ряда

(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.
Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.
Теорема Абеля позволяет дать описание области сходимости степенного ряда.
Теорема 1.2. Для степенного ряда (1.2) возможны только три случая:
1) ряд сходится в единственной точке x=0;
2) ряд сходится при всех значениях x;
3) существует
такое R>0,
что ряд сходится при всех значениях x,
для которых ![]() и
расходится при всех x,
для которых
и
расходится при всех x,
для которых ![]()
Определение 1.2. Интервал (-R,R), где число R определено в теореме 1.2, называется интервалом сходимости ряда (1.2), а число R – радиусом сходимости этого ряда.
Понятие
радиуса сходимости будет распространяться
на все три случая в теореме (3.2): для этого
в случае 1 условимся считать R=0,
а в случае 2 ![]()
На
практике радиус сходимости степенного
ряда чаще всего определяют с помощью
признака сходимости Даламбера.
Предположим, что все коэффициенты ряда
(1.2) отличны от нуля и существует
предел 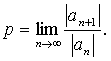 Тогда
радиус сходимости находится по формуле
Тогда
радиус сходимости находится по формуле ![]()
Действительно, в силу признака Даламбера ряд
![]()
сходится, если число
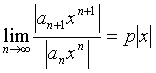
меньше
1, и расходится, если этот предел больше
1. Иначе говоря, ряд сходится для
всех x таких,
что 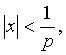 и
расходится при
и
расходится при 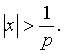 Это
и означает, что число
Это
и означает, что число ![]() является
радиусом сходимости ряда
является
радиусом сходимости ряда
28. Ряд Тейлора
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
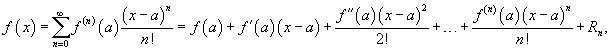
где Rn − остаточный член в форме Лагранжа определяется выражением
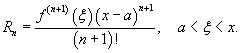
Если
приведенное разложение сходится в
некотором интервале x,
т.е. ![]() ,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
29. Разложение элементарных функций в ряд Маклорена. Применение степенных рядов в приближенных вычислениях
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если приведенное разложение сходится в некотором интервале x, т.е. , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена:
![]()
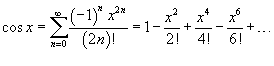 Разложение
некоторых функций в ряд Маклорена
Разложение
некоторых функций в ряд Маклорена