22.Числовой ряд с положительными членами.

1)Числовой ряд называется рядом с положительными членами, если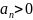 при любом n.

2) Любой ряд с положительными членами либо сходится и его сумма есть положительное число, либо расходится и его сумма равна + .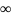

Доказательство: Пусть дан ряд с положительными членами . Запишем последовательность частичных сумм: S=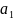 ; ;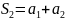 ; 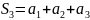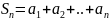. Таким образом , последовательность частичных сумм является строго возрастающей, но тогда возможны два случая:

1. Последовательность частичных сумм ограничена сверху. Это ознчает что ряд сходится.

2. Последовательность частичных сумм возрастает неограниченно, тогда ряд расходится.

23.Признак Даламбера сходимости ряда

Применять нужно, когда : 1. В общий член ряда входит какое-нибудь число в степени, например, 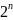, ,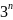  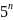и так далее. 2. В общий член ряда входит факториал.

Признак Даламбера: Рассмотрим положительный числовой ряд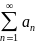 . Если существует предел отношения последующего члена к предыдущему: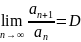 , то:

а) При D < 1 ряд сходится. В частности, ряд сходится при D = 0.

б) При D > 1 ряд расходится. В частности, ряд расходится при D = .

в) При D = 1 признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.

2) Интегральный признак сходимости ряда. Если f(x) – непрерывная , положительная и монотонно убывающая функция, то ряд 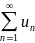где 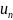= f(n) сходится или расзодится в зависимости от того, сходится или расходится интеграл .

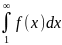Пример:

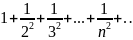
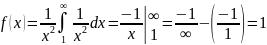– сходится интеграл, значит сходится и ряд.

24. Знакопеременные ряды

Ряд называется знакопеременным, если среди его членов имеются как положительные , так и отрецательные.

Теорема. Если знакопеременный ряд 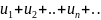таков что ряд составленный из абсолютных величин его членов, 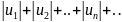сходится, то и данный знакопеременный ряд также сходится.

2) Абсолютная и условная сходимость

Ряд называется абсолютно сходящимся, если ряд 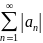также сходится.

Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

25. Знакочередующиеся ряды

 Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.

a₁ - a₂ + a₃ - a₄ + a₅ - ...    

2) Признак Лейбница

1.Ряд является знакочередующимся

2.Члены ряда убывают по модолю 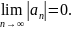Причем убыают монотонно. Если оба условия выполняются, то ряд сходится.

Вопрос 26. Ряды с функциональными числами. Точка сходимости и область сходимости

Ряд, членами которого являются функции от х, называется функциональным:

.

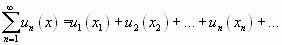
Придавая   определенное значение  , получим числовой ряд

,

который может быть как сходящимся, так и расходящимся.

Если полученный числовой ряд сходится, то точка х0 называется точкой сходимости функционального ряда; если же ряд расходится – точкой расходимости функционального ряда.

Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется егообластью сходимости.

В области сходимости функционального ряда его сумма является некоторой функцией от х: .

Определяется она в области сходимости равенством

, где

- частичная сумма ряда.