Вопрос 18.Решение квазилинейного диф. Уравнения в частных производных 1-го порядка.

Квазилинейным уравнением в частных производных первого порядка называется уравнение вида

                     ,            (1)

где   - функции, определенные в некоторой области переменных  . Для решения уравнения (1) нужно составить систему обыкновенных дифференциальных уравнений

 ,

интегрируя которую находим n независимых первых интегралов:

                                                                                        (2)

Общий интеграл уравнения (1) записывают в виде

,

где   - произвольная дифференцируемая функция.

В частности, если u входит только в один из первых интегралов (2), например в последний, то общее решение можно написать в виде:

         ,                                               (3)

где F - произвольная дифференцируемая функция. Разрешив равенство (3) относительно u, получим общее решение уравнения (1) в явном виде.

Вопрос 19

Нихуя

Вопрос 20. Понятие числового ряда

Числовой ряд – это сумма членов числовой последовательности вида  .

В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5:  .

 называют общим членом числового ряда или k–ым членом ряда.

Для предыдущего примера общий член числового ряда имеет вид  .

Частичная сумма числового ряда – это сумма вида  , где n – некоторое натуральное число.   называют также n-ой частичной суммой числового ряда.

К примеру, четвертая частичная сумма ряда   есть  .

Частичные суммы   образуют бесконечную последовательность частичных сумм числового ряда.

Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии  , то есть, будем иметь следующую последовательность частичных сумм:  .

Числовой ряд   называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд   называется расходящимся.

Суммой сходящегося числового ряда   называется предел последовательности его частичных сумм, то есть,  .

В нашем примере  , следовательно, ряд   сходится, причем его сумма равна шестнадцати третьим:  .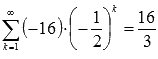

В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: 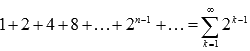 . n–ая частичная сумма определяется выражением  , а предел частичных сумм бесконечен:  .

Еще одним примером расходящегося числового ряда является сумма вида  . В этом случае n–ая частичная сумма может быть вычислена как  . Предел частичных сумм бесконечен  .

Сумма вида   называется гармоническим числовым рядом.

Сумма вида 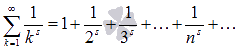 , где s – некоторое действительное число, называется обобщенно гармоническим числовым рядом.

21.Сходимость числового ряда

1)Числовой ряд 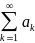называется сходящимся, если существует конечный предел последовательности частичных сумм S=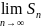 . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

2) (критерий Коши сходимости числового ряда)Для того, чтобы ряд сходился, необходимо и достаточно, чтобы ∀ε > 0 ∃N, ∀n > N,∀p ∈ N: 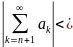ε

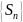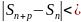Доказательство: Сходимость числового ряда —это сходимость последовательности его частичных сумм, а для сходимости последовательности , необходимо и достаточно, чтобы она была фундаментальной, т.е.∀ε>0∃N,∀n>N,∀p∈N: ε, или 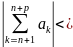ε , что и доказывает теорему.