Вопрос 12.

НИХУЯ

Вопрос 13. Линейное неоднородное дифференциальное уравнение со специальной правой частью; нахождение его частного решения, когда правая часть равна

Вопрос 14. Нормальная система диф. Уравнений 1-го порядка; структура общего решения системы линейных однородных диф. Уравнений 1-го порядка.

Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входят независимая переменная, искомые функции и их производные .Всегда предполагается, что число уравнений равно числу неизвестных функций.

Например, система двух дифференциальных уравнений 1-го порядка имеет вид:

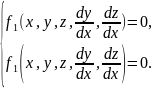
Решение этой системы дифференциальных уравнений состоит в нахождении функций y= y(x) и z = z(x) , удовлетворяющих обоим уравнениям системы.

Нормальной системой дифференциальных уравнений называется система дифференциальных уравнений 1-гопорядка, разрешённых относительно производной:

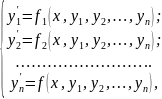
где х – независимая переменная, 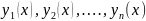− неизвестные функции.

Вопрос 15.Решение системы диф. Уравнений 1-го порядка методом вариации произвольных постоянных.

Метод вариации произвольных постоянных применяется для решения неоднородных дифференциальных уравнений. Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с непрерывными на [a; b] коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x),..., y_n(x) решений соответствующего однородного уравнения  

 y⁽ⁿ⁾ +a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) ,

где C₁(x), C₂(x) , ... , C_n(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y₁(x), y₂(x),..., y_n(x) — фундаментальная система решений однородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде

y*(x) = y(x,C₁,..., C_n) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) .

Неизвестные функции C₁(x), C₂(x) , ... , C_n(x) находятся из системы

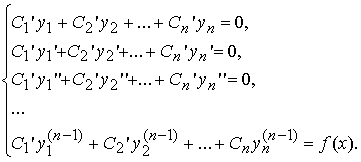
Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных или методом Лагранжа.

Вопрос 16

Нихуя

17. Квазилинейные дифференциальные уравнения в частных производных первого порядка; характеристики квазилинейного дифференциального уравнения.

Квазилинейным уравнением в частных производных первого порядка называется уравнение вида

                     ,            (1)

где   - функции, определенные в некоторой области переменных  . Для решения уравнения (1) нужно составить систему обыкновенных дифференциальных уравнений

 ,

интегрируя которую находим n независимых первых интегралов:

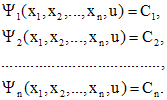                                                                                                                              (2)

Общий интеграл уравнения (1) записывают в виде

,

где   - произвольная дифференцируемая функция.

В частности, если u входит только в один из первых интегралов (2), например в последний, то общее решение можно написать в виде:

                                                          ,                                               (3)

где F - произвольная дифференцируемая функция. Разрешив равенство (3) относительно u, получим общее решение уравнения (1) в явном виде.

Пример 1. Найти общее решение уравнения

.

Решение.

Составляем систему дифференциальных уравнений

.

Ясно, что одним из первых интегралов этой системы будет  . Уравнение

является уравнением в полных дифференциалах, общее решение которого имеет вид  . Следовательно, еще один первый интеграл системы имеет вид  . Поскольку найденные первые интегралы являются линейно независимыми, то общий интеграл данного уравнения имеет вид

.

Разрешив последнее уравнение относительно u, получим общее решение в виде,

,

где f - произвольная дифференцируемая функция.

Чтобы найти поверхность  , удовлетворяющую дифференциальному уравнению

                                                                                                         (4)

и проходящую через данную линию

                                                     ,                                                                (5)

надо найти два независимых первых интеграла   системы(характеристической)

                                                               .                                                                            (6)

Поскольку вдоль каждой интегральной кривой характеристической системы функции   постоянны, а каждая интегральная кривая этой системы пересекается с заданной линией L, то

исключая из этой системы t, находим зависимость  , тем самым на интегральной кривой C справедливо соотношение

                                                                 .                                                                         (7)

В силу произвольности интегральной кривой соотношение (7) является представлением решения поставленной задачи.