10. Структура решения линейного неоднородного уравнения

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x)соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод вариации постоянных

Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.  Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).  Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений:

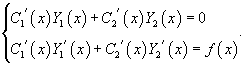
Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.  Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1. 

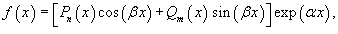2.   где P_n(x) и Q_m(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.  В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении.  В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.  Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Принцип суперпозиции

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида

то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части. 

Вопрос 11. Определение частного решения линейного неоднородного диф. Уравнения 2-го порядка методом вариации произвольных постоянных(метод Лагранжа).

Рассмотрим  линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами  b, c:                                          y''(x) + by'(x) + cy(x) = 0.                            (1)

Уравнение (1) имеет частное решение вида y(x) =  .  Коэффициент k удовлетворяет алгебраическому уравнению второго порядка                                            + bk + c = 0,                                             (2)

которое возникает после подстановки функции y(x) =   в уравнение (1).  Уравнение (2) имеет либо два различных корня  ,  , либо один кратный корень  .

В первом случае линейно независимые решения уравнения (1) имеют вид

                                y(x) =   (x) =    ,     y(x) =  (x) =            (3)  

Во втором случае линейно независимыми решениями являются функции                                 y(x) =   (x) =  ,       y(x) =  (x) = x          (4)

Линейная независимость решений означает, что не найдется такой константы С ≠ 0, что тождественно по x выполняется соотношение  (x) = С  (x).

И в первом, и во втором случае общее решение уравнения (1) может быть записано в виде линейной комбинации                                          y(x) =    (x) +     (x),                             (5)

где  ,   произвольные постоянные.

Метод вариации постоянных (метод Лагранжа) решения неоднородного дифференциального уравнения второго порядка                                       y''(x) + by'(x) + cy(x) = f(x)                               (6)

заключается в том, что решение уравнения (6) ищут в виде (5), но допускают зависимость  ,   от независимой переменной x, т.е. в виде                                       y(x) =  (x)  (x) +   (x)  (x).                        (7)

Найдем первую производную решения (7)                 y'(x) =  (x)  (x) +   (x)  (x) +  (x)  (x) +   (x)  (x).       (8)  

Потребуем, чтобы сумма первых двух членов в правой части формулы (8) была равна 0, т.е.                                (x)  (x) +   (x)  (x) = 0,                                (9) и, таким образом:                                y'(x) =  (x)  (x) +   (x)  (x).                          (10)

В силу (10) для второй производной функции y(x) имеем выражение                y''(x) =  (x)  (x) +   (x)  (x) +  (x)  (x) +   (x)  (x).  (11)

Подставляя (7), (10) и (11) в уравнение (6) и производя группировку членов, приходим к соотношению    (x)(a(x)  (x) + b(x)  (x) + c(x)  (x)) +   (x)(a(x)  (x) + b(x)  (x) + c(x)  (x)) + a(x)( (x)  (x) +   (x)  (x) ) =f(x)                                              (12)

В силу того, что функции  (x) ,  (x) решения линейного однородного уравнения (1), уравнение (12) принимает вид                                (x)  (x) +   (x)  (x) = f(x)                       (13)

Таким образом, для функций  (x),  (x) справедлива следующая система дифференциальных уравнений первого порядка                                    (x)  (x) +  (x)  (x) = 0,                                    (x)  (x) +   (x)  (x) = f(x)                       (14)

Из системы (14) можно найти, что           (x) =  ,                                

(x) =    .                (15)

Из (15) функции   (x),  (x) находятся интегрированием.

Если для уравнения (3) поставлена задача Коши, т.е. заданы начальные условия                                   y(0) =  , y'(0) =  ,                                                            (16)

то  для функций   (x),  (x) можно написать формулы                     (x) =  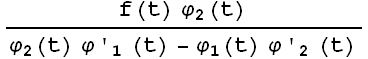dt  + α                (17)                       (x) =  dt  + β                 (18)

где α и β постоянные интегрирования. Они находятся подстановкой решения (7), в котором  (x),  (x) задаются формулами (17), (18), в начальные условия (16). В результате получаются алгебраические уравнения для α и β:                                          α  (0) + β  (0) =  ,                                          α  (0) + β  (0) =  .                                      (19)

Решая их, находим  α и β.