
- •Уравнение с разделяющимеся переменными
- •Однородные дифуравнения
- •Линейное уравнение первого порядка
- •Уравнение Бернулли.
- •Определение уравнения в полных дифференциалах
- •Дифуравнения второго порядка
- •Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами
- •Структура решения линейного неоднородного уравнения
- •Вопрос 11. Определение частного решения линейного неоднородного диф. Уравнения 2-го порядка методом вариации произвольных постоянных(метод Лагранжа).
- •Вопрос 12.
- •Вопрос 13. Линейное неоднородное дифференциальное уравнение со специальной правой частью; нахождение его частного решения, когда правая часть равна
- •Вопрос 14. Нормальная система диф. Уравнений 1-го порядка; структура общего решения системы линейных однородных диф. Уравнений 1-го порядка.
- •Вопрос 15.Решение системы диф. Уравнений 1-го порядка методом вариации произвольных постоянных.
- •Вопрос 16
- •17. Квазилинейные дифференциальные уравнения в частных производных первого порядка; характеристики квазилинейного дифференциального уравнения.
- •Вопрос 18.Решение квазилинейного диф. Уравнения в частных производных 1-го порядка.
- •Вопрос 19
- •Вопрос 20. Понятие числового ряда
- •21.Сходимость числового ряда
- •22.Числовой ряд с положительными членами.
- •23.Признак Даламбера сходимости ряда
- •24. Знакопеременные ряды
- •25. Знакочередующиеся ряды
- •Вопрос 26. Ряды с функциональными числами. Точка сходимости и область сходимости
- •Вопрос 27.Понятие степенного ряда. Теорема Абеля. Интервал сходимости.
- •1. Основные понятия. Область сходимости.
- •28. Ряд Тейлора
- •29. Разложение элементарных функций в ряд Маклорена. Применение степенных рядов в приближенных вычислениях
- •30. Тригонометрическая система функций. Коэффициенты Фурье функции, формулы Фурье Тригонометрическая система
- •31. Вещественная форма ряда Фурье
- •32. Достаточное условия разложимости функции в ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.
- •33. Разложение функции в ряд Фурье на отрезке произвольной длины
- •34. Ряд Фурье в комплексной форме
- •3 5. Интеграл Фурье как предельный случай ряда Фурье; вещественная форма интеграла Фурье
- •36. Интеграл Фурье в комплексной форме. Прямое и обратное преобразование Фурье.
- •37. Изображение функции по Лапласу. Простейшие свойства преобразования Лапаласа
- •38. Теоремы подобия, смещения и запаздывания операционного исчисления
- •39. Дифференцирование и интегрирование оригинала и изображения функции
- •40. Решение линейных дифференциальных уравнений с постоянными коэффициентами с помощью операционного исчисления
Дифференциальным уравнением называется уравнение, связывающее независимую переменную
 ,
искомую функцию
,
искомую функцию 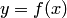 и
её производные
и
её производные 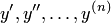 ,
т. е. уравнение вида
,
т. е. уравнение вида
![]()
Если
искомая функция ![]() есть
функция одной независимой переменной
,
дифференциальное уравнение
называется обыкновенным
есть
функция одной независимой переменной
,
дифференциальное уравнение
называется обыкновенным
Порядком дифференциального уравнения называют порядок старшей производной неизвестной функции, входящей в это уравнение.
Общим решением дифференциального уравнения называется функция y = фи (x, C1, C2,…, Cn), зависящая от n констант, если она является решением дифференциального уравнения при любых значениях постоянных C1, C2,…, Cn.
Частное решение дифференциального уравнения F (x, y, y',..., у (n))= 0, решение у = φ(х), получающееся из общего решения у = φ(х, C1,..., Cn) этого уравнения при некотором конкретном выборепроизвольных постоянных C1,..., Cn.
Например, общее решение уравнения у" + у = 0 есть у = C1cosx + C2sinx;полагая C1 = 2, C2 = —1, получим Ч. р. этого уравнения у = 2cosx — sinx.
Задачей Коши для дифференциального уравнения 1-го порядка, разрешенного относительно производной, называют задачу об отыскании решения уравнения, удовлетворяющего начальному условию:
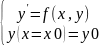
ИЛИ теорема Коши: Если функция f(х,y) и ее частная производная f'y(х,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (x0,y0) области G, в некоторой окрестности этой точки существует единственное решение уравнения у'=f(x,у), удовлетворяющее условиям:
у =у0 при х =х0
Уравнение с разделяющимеся переменными

Однородные дифуравнения

Линейное уравнение первого порядка
Линейное
уравнение первого порядка в
стандартной записи имеет
вид:
![]()
Решение таких уравнений осуществляется по следующей схеме:
1. Ищется решение дифференциального уравнения вида, которое называют линейным однородным дифференциальным уравнением 1го порядка.
v’ + pv=0;
2. В исходном уравнении совершается переход от переменной y к переменной u по формулам
y =uv, y’=u’v+uv’
3. Полученное для переменной u уравнение решается так:
u’v+uv’+puv
=q
=>u’v+u(v’+pv)
=q
=>u’v
= q
=>u’
=
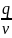 =>
=>
u
=
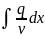 ;
;
Уравнение Бернулли.
Дифференциальные уравнения вида
![]() ,
,
где p=p(x), q=q(x), а n − любое число, отличное от 1, называют уравнениями Бернулли.
Если n = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда n = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки
![]()
Новое дифференциальное уравнение для функции z(x) имеет вид
![]() -
линейноедифуравнение
первого порядка
-
линейноедифуравнение
первого порядка
Определение уравнения в полных дифференциалах
Дифференциальное уравнение вида
![]()
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение
![]()
Общее решение уравнения в полных дифференциалах определяется формулой
![]()
где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
![]()
Алгоритм решения уравнения в полных дифференциалах
Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
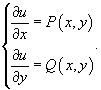
Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
![]()
Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
![]()
Отсюда получаем выражение для производной неизвестной функции φ(y):
![]()
Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
Общее решение уравнения в полных дифференциалах записывается в виде:
![]()
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ(x).
Дифуравнения второго порядка
В общем случае дифференциальное уравнение второго порядка можно записать в виде
![]()
где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:
![]()
В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такиенеполные уравнения включают в себя 5 различных типов:
![]()
С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y'';
Функция F(x, y, y', y'') является точной производной функции первого порядка Ф(x, y, y').
Итак, рассмотрим указанные случаи понижения порядка более подробно.
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение y'' = f(x), то его порядок можно понизить введением новой функции p(x), такой, чтоy' = p(x). В результате мы получим дифференциальное уравнение первого порядка
![]()
Решая его, находим функцию p(x). Затем решаем второе уравнение
![]()
и получаем общее решение исходного уравнения.
Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p(y), полагаяy' = p(y). Тогда можно записать:
![]()
и уравнение принимает вид:
![]()
Решая его, находим функцию p(y). Затем находим решение уравнения y' = p(y), то есть функцию y(x).
Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию y' = p(x) и получаем уравнение
![]()
которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p(x) и затем функцию y(x).
Случай 4. Уравнение вида y''= f (x,y' )
Используем подстановку y' = p(x), где p(x) − новая неизвестная функция, и получаем уравнение первого порядка
![]()
Интегрируя, определяем функцию p(x). Далее решаем еще одно уравнение 1-го порядка
и находим общее решение y(x).
Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию p(y), полагая y' = p(y). Дифференцирование этого равенства по x приводит к уравнению
![]()
В результате наше исходное уравнение записывается в виде уравнения 1-го порядка
![]()
Решая его, находим функцию p(y). Затем решаем еще одно уравнение первого порядка
![]()
и определяем общее решение y(x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.
Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''
Если левая часть дифференциального уравнения
![]()
удовлетворяет условию однородности, т.е. для любого k справедливо соотношение
![]()
то порядок уравнения можно понизить с помощью подстановки
![]()
После нахождения функции z(x) исходная функция y(x) находится интегрированием по формуле
![]()
где C2 − постоянная интегрирования.
Случай 7. Функция F(x, y, y', y'') является точной производной
Если удается найти такую функцию Ф(x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству
![]()
то решение исходного уравнения представляется интегралом
![]()
Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.
