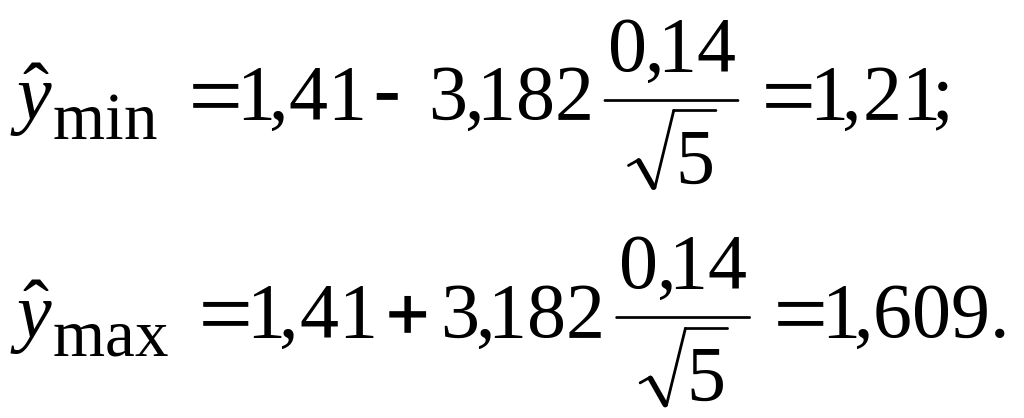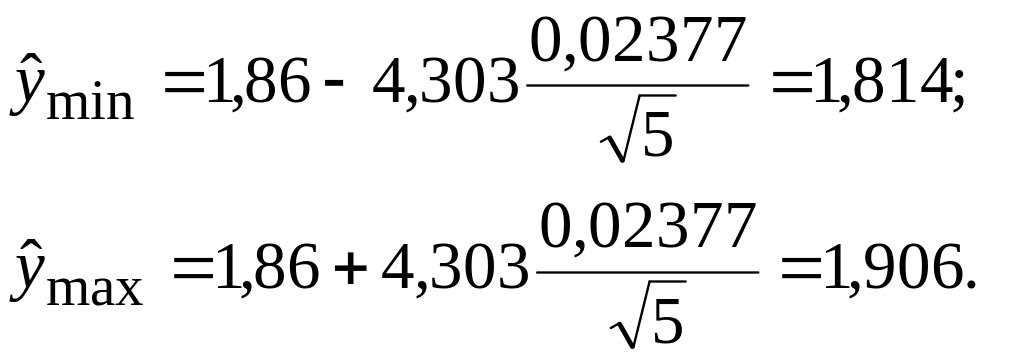Пример 2.
Для
рассмотренных выше данных о строительстве
жилья построим интервальный прогноз
объемов строительства жилья на 2008 г.,
используя две функции тренда: линейную
и параболу
.
Соберем ранее рассчитанные выровненные
уровни ряда динамики (колонки 9 и 10
таблицы 1, с. 2) в табл. 3.
Таблица 3
Параметры для построения интервального прогноза
Годы
|
Объемы жилищного строительства, млн. кв.м |
Условные обозначения периодов |
Выровненные уровни динамики, млн. кв. м (прямая) |
Квадраты отклонений фактических и рассчитанных значений (прямая) |
Выровненные уровни динамики, млн. кв. м (парабола) |
Квадраты отклонений фактических и рассчитанных значений (парабола) |
i |
yi |
ti |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
2003 |
2,9 |
-2 |
2,76 |
0,0196 |
2,89 |
0,000121 |
2004 |
2,4 |
-1 |
2,49 |
0,0081 |
2,43 |
0,000676 |
2005 |
2,1 |
0 |
2,22 |
0,0144 |
2,09 |
0,000081 |
2006 |
1,9 |
+1 |
1,95 |
0,0025 |
1,89 |
0,000196 |
2007 |
1,8 |
+2 |
1,68 |
0,0144 |
1,81 |
0,000081 |
2008 |
- |
+3 |
|
|
|
|
Итого |
11,1 |
0 |
11,1 |
0,0590 |
11,10 |
0,001155 |
Таблица 4
Построение интервального прогноза
Подход 1
тренд
– линейная функция:
|
Подход 2
тренд
– парабола второго порядка:
|
1. Точечная экстраполяция.
Найдем
|
|
Прогноз строительства жилья в 1995 г. 1,41 млн. кв. м |
Прогноз строительства жилья в 1995 г. 1,86 млн. кв. м |
2. Поиск доверительного интервала, Пусть задана вероятность попадания в интервал p=0,95%
Величины
|
|
уровень значимости a: a=100%-p=5%. n=5 – число уровней ряда; m=2 – число параметров в уравнении тренда; k=n-m=3 – количество степеней свободы; ta =3,182 – табличное значение t-критерия Стьюдента. |
уровень значимости a: a=100%-p=5%. n=5 – число уровней ряда; m=3 – число параметров в уравнении тренда; k=n-m=2 – количество степеней свободы; ta =4,303 – табличное значение t-критерия Стьюдента. |
;
для этого подставим в функцию тренда
t=3
рассчитаны в
итоге колонки 2, а
величины
для
линейного тренда и параболы в итогах
колонок 5 и 7 таблицы 3.Продолжение таблицы 4
– величина среднеквадратического
отклонения
от тренда:
Величина доверительного интервала
Вывод: Таким образом, с вероятностью 95% можно ожидать, что в 1995 г. жилищно-строительные кооперативы построят жилья не меньше чем 1,21 млн. кв. м, но не больше 1,609 млн. кв. м. Относительная ошибка уравнения
где
( |
– величина среднеквадратического отклонения от тренда:
Величина доверительного интервала
Вывод: Таким образом, с вероятностью 95% можно ожидать, что в 1995 г. жилищно-строительные кооперативы построят жилья не меньше чем 1,814 млн. кв. м, но не больше 1,906 млн. кв. м. Относительная ошибка уравнения
где ( ). |
Очевидные различия выводов, полученных при первом и втором подходах объясняются видом кривой, характеризующей тенденцию развития жилищного строительства. Применение метода конечных разностей показывает, что парабола более пригодна для выравнивания данного динамического ряда. Об этом свидетельствует и величина относительной ошибки уравнения: для параболы второго порядка она равна 1,07%, что существенно меньше, чем для линейной функции (6,32%). Графическая интерпретация тренда и прогноза представлена на рис. 1. |
|
).
Рис. 1. Интервальный прогноз объемов строительства жилья
по линейному и параболическому тренду