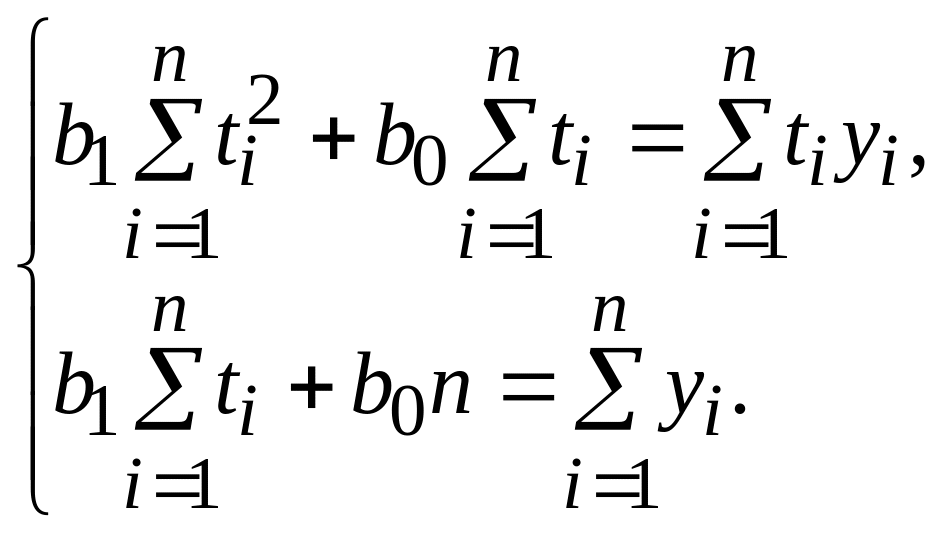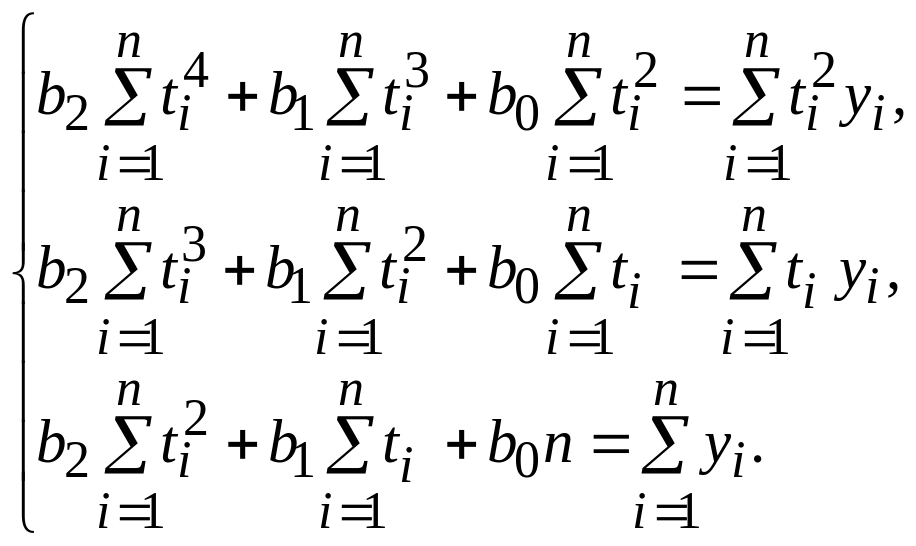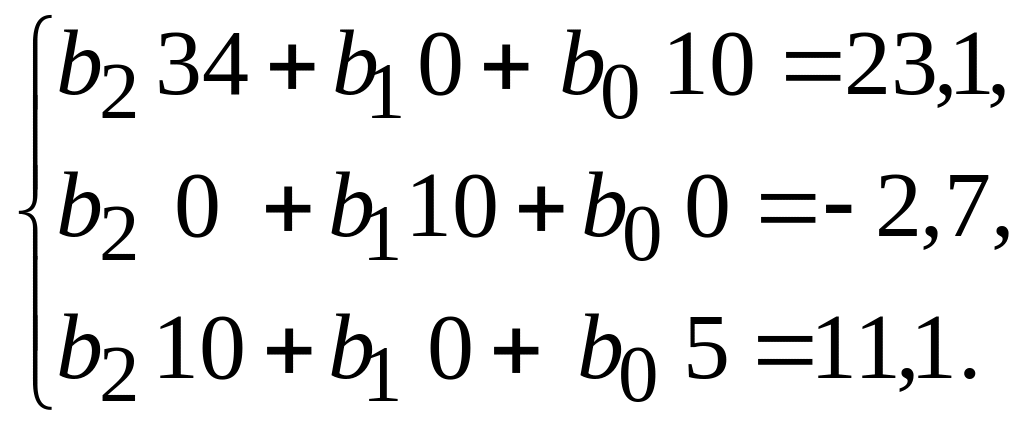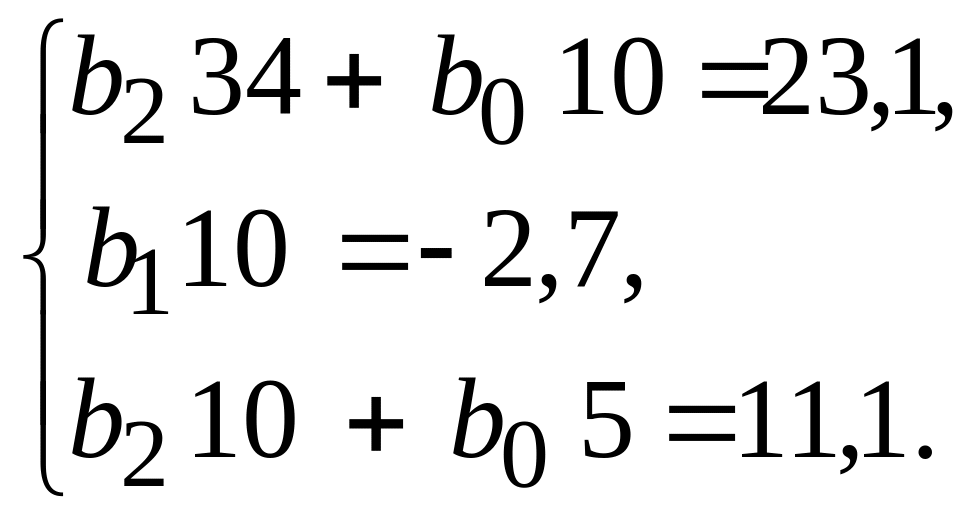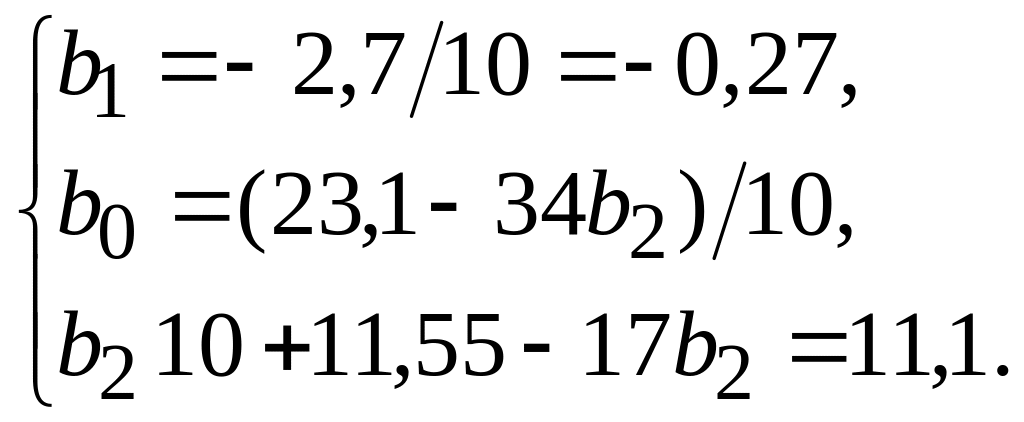4.4. Определение параметров функции тренда. Точечный прогноз

Если вид функции тренда выбран, то параметры функции b₀, b₁ и др. можно рассчитать по методу наимень­ших квадратов. Ниже представлены системы уравнений для трех основных видов функций.

а) Линейный тренд y=b0+b1t. Параметры определяются из системы:

б) Параболический тренд y=b0+b1t+bа2t2. Параметры определяются из системы:

в) Показательный тренд y=b₀·t^b1.

Параметры определяются следующим образом:

→ z=c₀ + c₁·v.

Параметры с₀, с₁ находятся как для линейной функции регрессии относительно логарифмов исходных данных t и y. Затем b₀=е^с0, b₁= с₁.

Поиск параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю. Для этого:

• при нечетном числе уровней ряда динамики, уровень, находящийся в середине ряда, принимается за условное начало от­счета времени (0). Даты, стоящие выше этого уровня, обозначаются (-1,-2, -3 и т.д.), а ниже – (+1, +2, +3 и т.д.).

• при четном числе уровней ряда динамики, периоды вре­мени верхней половины ряда (до середины) нумеруются -1,-3,-5 и т.д., а нижней +1,+3,+5, и т.д. Тогда ∑t_i=0 будет равна нулю.

Пример 1. Рассмотрим аналитическое выравнивание ряда ди­намики объемов строительства жилья жилищно-строительными коопера­тивами в России. Исходные данные и расчет параметров систем урав­нений линейного и параболического трендов представлены в таблице.

Таблица 1

Исходные данные и параметры систем уравнений трендов

Годы	Объемы стро­и­­тельства жилья, млн. кв.м	Условные обозначения периодов						Выровненные уровни ряда, млн. кв. м прямая	Выровненные уровни ряда, млн. кв. м прабола
i	yi	ti	yiti	ti2	ti3	yiti2	ti4
1	2	3	4	5	6	7	8	9	10
2003	2,9	-2	-5,8	4	8	11,6	16	2,76	2,89
2004	2,4	-1	-2,4	1	1	2,4	1	2,49	2,43
2005	2,1	0	0	0	0	0	0	2,22	2,09
2006	1,9	+1	1,9	1	-	1,9	1	1,95	1,89
2007	1,8	+2	3,6	4	-8	7,2	16	1,68	1,81
Итого	11,1	0	-2,7	10	0	23,1	34	11,1	11,1

Колонки 3-8 таблицы 1 заполнены в соответствии с параметрами систем уравнений для линейного и параболического трендов, представленными на с. 1.

1) Используя итоги колонок 2-5, определим систему уравнений и параметры линейного тренда:

Таким образом, тренд ряда динамики объемов жилищного строительства может быть представлен прямой: .

Используя приведенное уравнение, рассчитаем для каждого года оценки фактических данных по тренду и заполним колонки 6, 7 и 8:

для 2003 г. ;

для 2004 г. ; и т.д.

Для расчета прогнозной оценки на 2008 г. подставим в уравнение тренда соответствующее значение t, которое в данном случае будет равно 3:

для 2008 г. .

2) Используя итоги колонок 2-8, определим систему уравнений и параметры параболического тренда:

b₀=2,0914; b₁=- 0,27; b₂=0,0643.

Таким образом, динамика объемов жилищного строительства может быть представлена параболическим трендом:

.

Подставляя в данное уравнение значения t определим оценки фактических данных по параболическому тренду (выровненные уровни ряда динамики) и заполним колонку 10 таблицы 1.

Проверка правильности расчета уровней выравниваемого ряда дина­мики: сумма зна­чений эмпирического ряда должна совпадать с суммой вычисленных уровней выровненного ряда (итоги колонок 2 и 9 для линейной функции и колонок 2 и 10 для параболы).