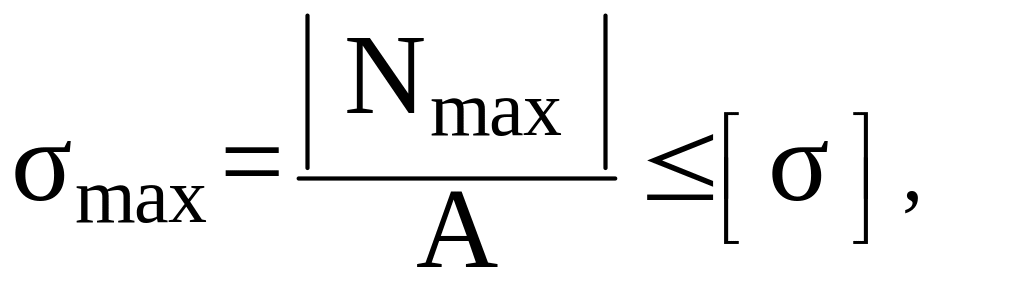Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

“Уфимский государственный нефтяной

технический университет”

Кафедра “Оборудование предприятий нефтехимии и нефтепереработки”

РАсчетно-проектировочные работы

по сопротивлению материалов и механике

Расчеты при простых деформациях

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

для самостоятельной работы студентов

Уфа 2010

В учебно-методическом пособии приведены теоретические предпосылки, примеры решения задач, а также исходные данные и схемы для выполнения расчетно-проектировочных работ по сопротивлению материалов и механике. Перечень решаемых задач охватывает начальную часть указанных дисциплин и соответствует учебным планам образовательной программы механического (специальность 240801 “Машины и аппараты химических производств”) и немеханического (специальность 240403 “Химическая технология природных энергоносителей и углеродных материалов”) профилей.

В пособии рассмотрены вопросы проведения расчетов на прочность при простых деформациях (растяжении – сжатии и кручении). Наличие многовариантности предлагаемых к решению задач позволяет составлять расчетные задания, соответствующие рабочим программам названных специальностей.

Составители: Газиев Р.Р., доцент, канд. техн. наук

Захаров Н.М., доцент, канд. техн. наук

Рецензенты Амиров И.З., главный конструктор

ОАО ”Салаватнефтемаш”

Баширов М.Г., профессор, д-р техн. наук

 Уфимский государственный нефтяной технический университет, 2010

ОБЩИЕ ТРЕБОВАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ

1 Вариант задания и перечень задач расчетно-проектировочной работы (РПР) выдается преподавателем.

2 Перед выполнением РПР следует изучить теоретический материал соответствующего раздела курса и приобрести необходимые навыки решения задач и их оформления в соответствии с нормативными документами.

3 Каждая РПР оформляется согласно ГОСТ 2.105-95 ЕСКД. “Общие требования к текстовым документам” черными чернилами, пастой или тушью, рукописным, машинописным текстом или на ЭВМ. РПР состоит из пояснительной записки с титульным листом и графической части.

3.1 Каждая задача РПР начинается с новой страницы, на которой указывается номер и название задачи, задание и порядок решения, исходные данные и заданная исходная схема (согласно варианту).

3.2 На последующих страницах выполняется решение задачи, основные этапы которого сопровождаются краткими пояснениями с указанием использованных библиографических источников, расчетными схемами, рисунками, эскизами и таблицами.

3.3 Расчетная схема и основные результаты решения представляются в графической форме на отдельной странице, которая может быть размещена после задания или в конце пояснительной записки (может быть увеличенного формата в виде приложения). Эпюры внутренних силовых факторов, напряжений и перемещений изображаются строго под расчетной схемой на той же странице.

3.4 Каждый этап решения задач выполняется в аналитической форме. Числовые значения подставляются только в окончательные выражения в основных единицах системы СИ с соблюдением правил ведения технических записей (см. решения примеров).

3.5 При повторном представлении РПР на проверку после исправления указанных замечаний следует сохранять все листы с пометками преподавателя.

1 Растяжение и сжатие

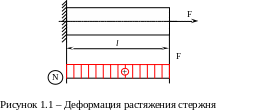
Центральным растяжением или сжатием называется такой вид деформации, при котором в сечении бруса, называемого стержнем, возникает только один внутренний силовой фактор – продольная сила N_z (рисунок 1.1).

При растяжении-сжатии в поперечных и наклонных сечениях стержня возникают как нормальные , так и касательные  напряжения. Рассмотрим их более подробно.

1.1 Напряжения в поперечных сечениях стержня

Получим зависимость для нормального напряжения, которое возникает в поперечных сечениях стержня. Для этого рассмотрим следующие стороны задачи о растяжении стержня с постоянной площадью поперечного сечения А.

Статическая сторона задачи. Используем интегральное уравнение равновесия, связывающее между собой продольную силу N_z и нормальное напряжение _z, возникающее в поперечном сечении стержня

Чтобы из данного уравнения получить зависимость для нахождения нормального напряжения _z, необходимо провести анализ напряженно-деформированного состояния стержня, т.е. установить закон изменения деформаций и напряжений в поперечном сечении стержня.

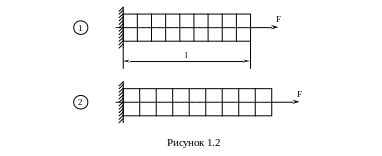
Геометрическая сторона задачи. Нанесем на поверхность стержня перпендикулярно к продольной оси сетку с постоянным шагом. После нагружения бруса можно видеть, что линии сетки перемещаются с одинаковым приращением параллельно самим себе, оставаясь прямыми и перпендикулярными к оси стержня (рисунок 1.2). Анализ деформации стержня показывает, что при растяжении-сжатии является справедливой гипотеза плоских сечений (гипотеза Бернулли): поперечные сечения стержня, плоские до деформации, остаются плоскими и после деформации, перемещаясь поступательно вдоль его продольной оси.

На основании этого можно считать, что продольные волокна стержня удлиняются на одну и ту же величину. Следовательно, в поперечных сечениях стержня продольные деформации и нормальные напряжения распределяются равномерно, т.е. по постоянному закону

Преобразуем (1.1) с учетом (1.2), имеем

Выражая нормальное напряжение _z из (1.3), получим

Таким образом, при растяжении-сжатии в поперечных сечениях стержня возникают нормальные напряжения, определяемые отношением продольной силы к площади сечения.

Зависимость (1.4) является справедливой только при определенных условиях, обусловленных принципом Сен-Венана. Принцип Сен-Венана: на некотором удалении от места приложения нагрузки напряжения не зависят от способа приложения нагрузки и определяются по величине равнодействующей этой нагрузки (рисунок 1.2).

Аналогично принципу Сен-Венана резкое изменение напряжений, т.е. концентрация напряжений, наблюдается в местах, где изменяется поперечный размер сечения бруса. Таким образом, концентраторами напряжения являются отверстия, различные выточки, ступенчатые переходы, шпоночные канавки и т.д. (рисунок 1.3). Для учета концентраций напряжений в формуле (1.4) площадь берется с учетом ослабления А_нетто, т.е.

здесь А_нетто – “нетто” площадь определяемая с учетом ослабления по формуле

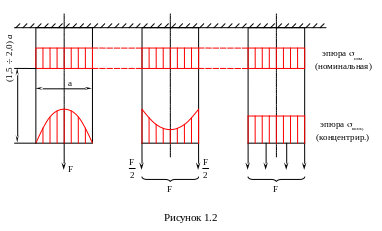
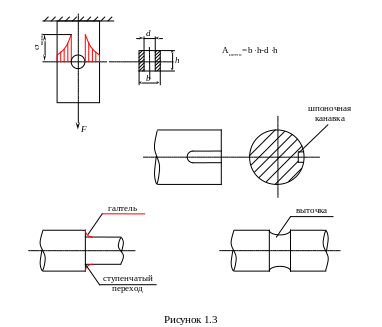
Таким образом, в поперечных сечениях растянутого или сжатого стержня возникают нормальные напряжения, определяемые по зависимостям (1.4) и (1.5).

1.2 Напряжение в наклонных сечениях стержня

Выделим в растянутом стержне (рисунок 1.4) два сечения – поперечное (I–I) с площадью A и наклонное (II–II) с площадью A_ ,связанные зависимостью

В наклонном сечении (II–II) возникает продольная сила N_z, которую удобно разбить на две составляющие к сечению (II–II) – нормальную N_ и касательную T_

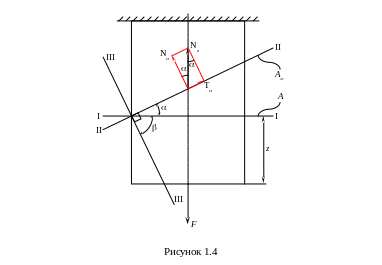
В наклонном сечении возникают нормальные и касательные напряжения, определяемые следующим образом:

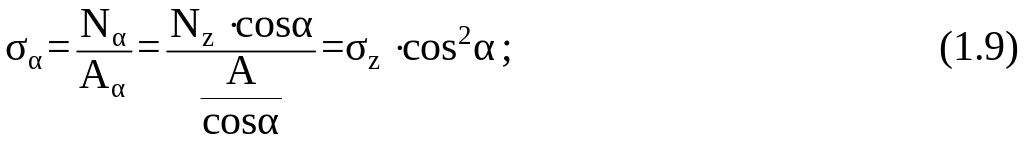
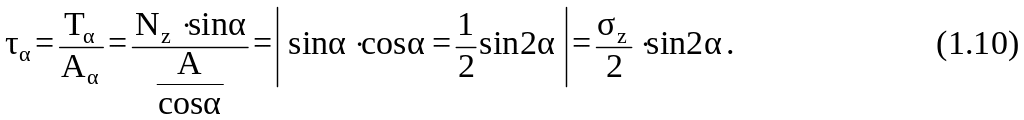
Анализируя зависимости (1.9) и (1.10), видим, что нормальные и касательные напряжения ( и ) будут максимальны при следующих углах:

Полученные условия позволяют объяснить характер разрушения многих элементов конструкций по схеме нормального отрыва или по схеме смещения или касательного сдвига (рисунок 1.5).

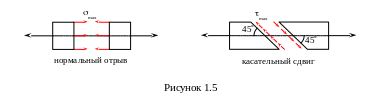
Проведем еще одно наклонное сечение (III–III) под углом  к поперечному сечению (I–I) или перпендикулярно к сечению (II–II), причем

Определим напряжения, действующие в сечении (III–III), для чего воспользуемся зависимостями (1.9), (1.10) и (1.11):

Сложим нормальные напряжения, действующие в сечениях (II–II) и (III–III), получим

Зависимость (1.14) выражает закон суммы нормальных напряжений: сумма нормальных напряжений, действующих на двух взаимно перпендикулярных площадках, есть величина постоянная и равная максимальному нормальному напряжению, возникающему в поперечных сечениях растянутого стержня.

Сложим касательные напряжения, действующие в сечениях (II–II) и (III–III), получим

или

(1.15)

Зависимость (1.15) выражает закон парности касательных напряжений: касательные напряжения, действующие на двух взаимно перпендикулярных площадках, равны по величине и противоположны по направлению (рисунок 1.6).

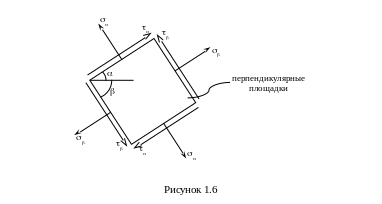
1.3. Деформации и перемещения. Закон Гука при растяжении или сжатии

При растяжении-сжатии возникают продольные и поперечные деформации. Рассмотрим их более подробно (рисунок 1.7).

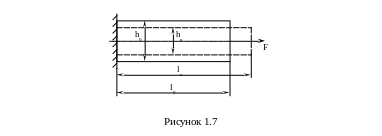
Здесь:

l₀ и h₀ – продольные и поперечные размеры стержня до деформации, м;

l_к и h_к – продольные и поперечные размеры стержня после деформации, м;

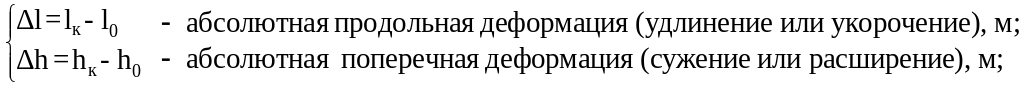
Относительные деформации  и  – величины безразмерные или могут измеряться в процентах.

Отношение поперечной деформации к продольной является константой материала, которая называется коэффициентом поперечной деформации или коэффициентом Пуассона

Для реальных материалов коэффициент Пуассона изменяется в следующих пределах

0   0,5.

Так, этот коэффициент равен для

- пробкового дерева  = 0;

- для стали  = 0,3;

- каучука  = 0,5.

При помощи коэффициента Пуассона можно определить поперечную деформацию через продольную и наоборот

Продольная деформация и нормальные напряжения при растяжении-сжатии связаны между собой законом линейной пропорциональности, который называется законом Гука - продольные деформации изменяются пропорционально изменению нормальных напряжений

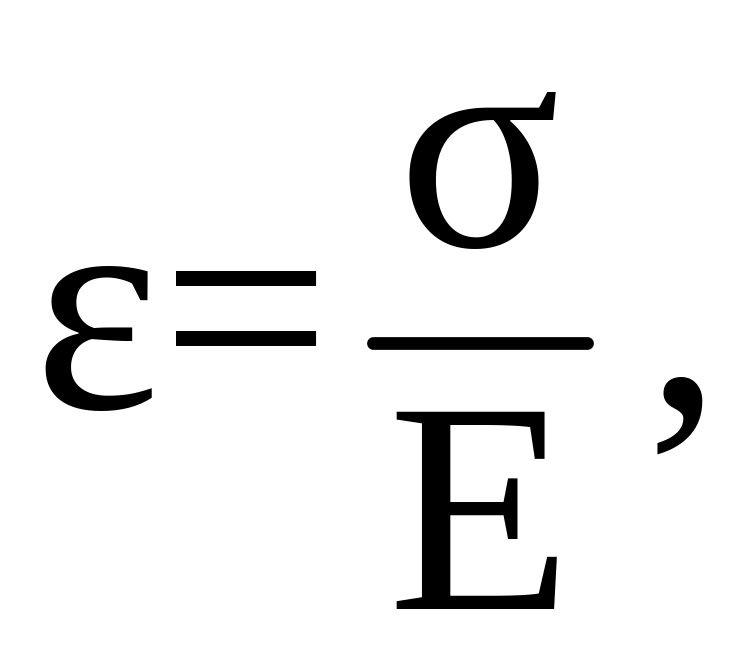
(1.18)

где E – модуль упругости первого рода (или модуль Юнга) – это физическая постоянная материала, характеризующая его упругие свойства, численно равная нормальному напряжению, которое вызывает деформацию, равную единице

Модуль упругости первого рода принимает значение для:

- стали Е_сталь = (1,9…2.2)10⁵ МПа;

- чугуна Е_чугун = 1,210⁵ МПа

Закон Гука (1.18) иногда применяется и в таком виде

 = Е .

(1.20)

Пользуясь законом Гука, получим зависимость для нахождения абсолютных деформаций при растяжении-сжатии

здесь EA - жесткость сечения стержня, .

Зависимость (1.21) выражает закон Гука для абсолютной деформации при растяжении-сжатии.

При нахождении полной деформации ступенчатого стержня (рисунок 1.8) определяют сумму деформаций отдельных ступеней стержня по формуле

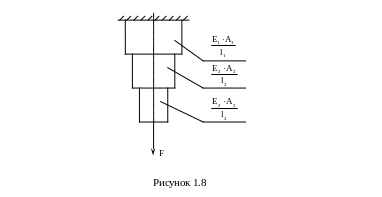
Если стержень имеет переменное сечение и по длине нагружен переменной нагрузкой, например, собственным весом (рисунок 1.9), то его полная деформация определяется в интегральной форме

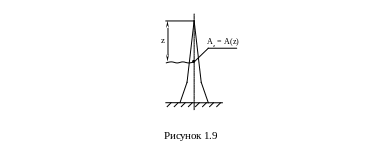
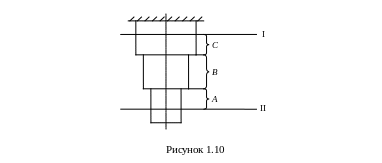
В некоторых случаях возникает необходимость в нахождении перемещений точек стержня по отношению к какому-либо сечению (например, к месту закрепления). В этом случае перемещение, представляющее собой изменение местоположения искомого сечения, найдется как абсолютная деформация участка бруса, заключенного между заданными сечениями (рисунок 1.10)

(1.24)

1.4 Потенциальная энергия упругой деформации

Довольно часто приходится оценивать напряженно-деформированное состояние с позиции работы или энергии, затраченной на деформирование. В случае растяжения или сжатия работа деформирования, переходящая в потенциальную энергию упругой деформации, найдется как произведение средней продольной силы на создаваемую деформацию стержня,

где U – потенциальная энергия упругой деформации, Дж;

P – работа внешней силы, Дж;

F – внешняя сила, Н, по величине которой определяется продольная сила, причем F = N.

Тогда, с учетом (1.22), получим

Потенциальная энергия упругой деформации равна площади диаграммы растяжения (рисунок 1.11).

Для оценки энергетических свойств материала нагруженного стержня полученную потенциальную энергию упругой деформации относят к объему стержня, то есть определяют удельную потенциальную энергию упругой деформации

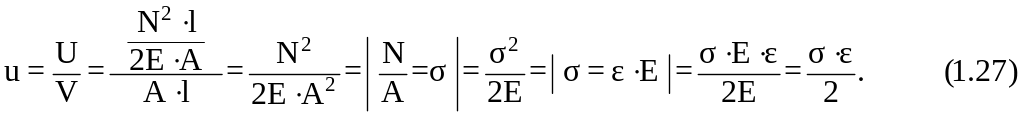
Удельную потенциальную энергию упругой деформации графически можно интерпретировать как площадь диаграммы упругого растяжения (рисунок 1.12)

По величине потенциальной энергии упругой деформации можно судить о способности материала стержня сопротивляться динамическим и ударным нагрузкам.

1.5 Экспериментальное изучение механических свойств материалов. Испытание на растяжение

Экспериментальные исследования выполняются с целью изучения механических свойств материалов, проверки точности расчетных формул, оценки работоспособности проектируемой конструкции на лабораторных моделях. Лабораторные испытания материалов производят при различных деформациях таких, как растяжение, сжатие, сдвиг, кручение, изгиб.

Одним из наиболее важных видов экспериментальных исследований является одноосное испытание на растяжение, т.к. при этом определяются наиболее важные механические характеристики материалов. Для испытания применяются лабораторные образцы цилиндрической формы (рисунок 1.13) или плоской формы (рисунок 1.14), размеры и режим нагружения которых соответствуют ГОСТ 1497-84.

Для испытаний на растяжение применяют разрывные машины, позволяющие в процессе испытания определять усилия и соответствующие им деформации образца. В результате проведенного испытания получают диаграмму растяжения, в которой по оси ординат откладываются усилия, а по оси абсцисс – соответствующие им удлинения. Типичный вид такой диаграммы для малоуглеродистой стали изображен на рисунке 1.15.

После обработки экспериментальных данных определяются механические характеристики прочности и пластичности. К характеристикам прочности, МПа, относятся:

- предел пропорциональности σ_пц;

- предел упругости σ_уп;

- предел текучести σ_т;

- предел прочности σ_в ,;

- напряжение в момент разрыва - условное и истинное σ_р^у, σ_р^и .

К характеристикам пластичности, %, относятся:

- относительное удлинение при разрыве δ;

- относительное сужение при разрыве ψ.

Также определяются энергетические характеристики материала:

- полная работа, затраченная на разрушение образца Р, Дж;

- удельная работа, затраченная на разрушение образца р, Дж/м³.

Основными характеристиками прочности материалов, которые используются в практических расчетах как предельные напряжения, являются предел временного сопротивления разрыву (предел прочности) и предел текучести .

Предел текучести является напряжением, опасным обычно для пластичного материала, а предел прочности - для хрупкого.

1.6 Основные принципы расчета элементов конструкции. Условия и виды расчетов при растяжении-сжатии

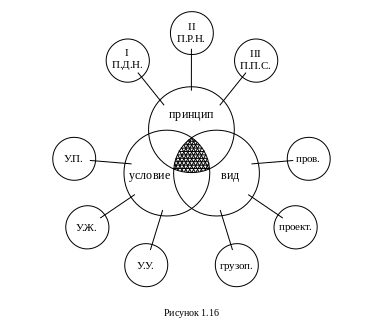
В курсе сопротивления материалов расчет элементов конструкций выполняется по различным условиям с применением трех основных принципов расчета и рассмотрением трех видов расчета. Принципы, условия и виды расчетов можно схематически представить следующим образом (рисунок 1.16):

I принцип расчета: – принцип допускаемых напряжений (П.Д.Н.) – принимает в качестве критерия работоспособности конструкции наибольшее напряжение, которое не должно превышать допускаемого значения материала этой конструкции, т.е.

,

где [] (или [τ]) – допускаемое напряжение, МПа, превышение которого (с некоторым запасом) может привести к разрушению конструкции; оно определяется как отношение предельного напряжения _пред к коэффициенту запаса прочности n

(1.29)

В качестве предельного напряжения принимается:

– для пластичного материала – предел текучести _т,с целью предотвращения появления остаточных деформаций,;

– для хрупкого материала – предел прочности _в, с целью предотвращения полного разрушения материала.

Коэффициент запаса прочности принимается по нормативным документам или с учетом разнообразных факторов проектируемой конструкции. К этим факторам можно отнести: ответственность конструкции, срок ее эксплуатации, точность нахождения действующих нагрузок, правильность расчетных формул и т.д.

Коэффициент запаса прочности всегда превышает единицу и выбирается в зависимости от материала следующим образом:

n_пласт = 1,5 - 2,0;

n_хруп = 1,8 - 2,5,

Принцип допускаемых напряжений широко применяется в курсе сопротивления материалов в силу своей простоты.

II принцип расчета – принцип разрушающих нагрузок (П.Р.Н.) – принимает в качестве критерия работоспособности наибольшую нагрузку в элементе конструкции, которая не должна превышать допустимой нагрузки

где [F] – допускаемая нагрузка, Н, определяемая как

Предельная нагрузка выбирается в зависимости от материала для случая растяжения-сжатия из условия

(1.32)

При расчете статически определимых систем первым или вторым принципом получают одинаковые значения искомых параметров, а в случае решения статически неопределимых систем расчет по первому принципу является более надежным, а по второму – более экономичным.

III принцип расчета: – принцип предельных состояний (П.П.С.) – производится по соответсвующим нормативным документам, в которых учитываются разнообразные факторы, влияющие на работоспособность или предельное состояние конструкции (например, ГОСТы, СНиПы, ТУ, МР, СТП). В курсе сопротивления материалов данный принцип расчета применяется редко.

В каждом принципе расчета используются условия расчета, которые обусловливают предельные величины параметров напряженно-деформированных состояний. В курсе сопротивления материалов расчет выполняется по условиям прочности, жесткости или устойчивости. Рассмотрим более подробно условия прочности и жесткости для случая растяжения или сжатия.

Для растянутого или сжатого стержня должны выполняться следующие условия прочности и жесткости:

(1.33)

(1.34)

По условиям (1.33) и (1.34) можно выполнить три основных вида расчетов: проверочный, проектировочный и нахождение максимальной грузоподъемности конструкции.

Рассмотрим эти виды расчетов на примере условия прочности (1.33):

- при проверочном расчете по известной внешней нагрузке, размерах и материале конструкции производится проверка выполнения условия (1.33);

- при проектировочном расчете по известной внешней нагрузке, и материале определяются размеры конструкции по условию

- при расчете максимальной грузоподъемности по известным размерам и материалу определяется максимальная нагрузка, воспринимаемая конструкцией, по условию

При выполнении расчетов одновременно по условию прочности и условию жесткости в конечном итоге выбирается то значение искомого параметра, которое одновременно отвечает как условию прочности, так и условию жесткости, например

.

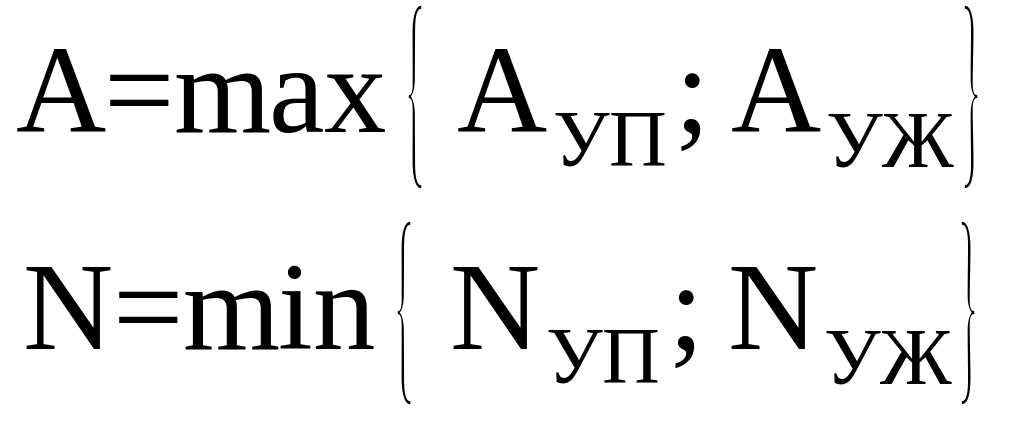1.7 Статически неопределимые системы при растяжении - сжатии

Статически неопределимой системой называется система, в которой число неизвестных усилий (например, реакций связи) превышает число уравнений статики. Степень статически неопределимой системы представляет собой разность между числом неизвестных усилий и числом уравнений статики

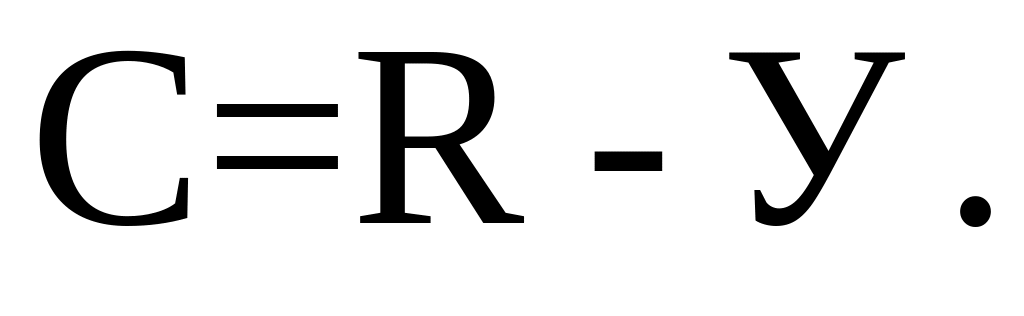
(1.36)

Система, изображенная на рисунке 1.17, считается статически неопределимой, так как для этой системы можно составить только три уравнения статики, а неизвестных реакций связи четыре, т.е.

С = 4 – 3 = 1.

В статически неопределимой системе существуют так называемые «лишние» связи, устранение которых не нарушает геометрической неизменяемости всей системы, т.е. не превращает систему в механизм.

Степень статически неопределимой системы характеризует число «лишних» связей системы, и тем самым обуславливает количество дополнительных уравнений, необходимых для раскрытия статической неопределимости системы.

Статически неопределимые системы являются более прочными, жесткими и устойчивыми, однако обладают рядом особенностей, которые принято представлять в виде трех основных свойств

– свойство жесткости – усилия в элементах статически неопределимых систем распределяются пропорционально их жесткости независимо от абсолютных размеров этих элементов;

– свойство о монтажных напряжениях – при неточном изготовлении или сборке элементов статически неопределимых систем в них возникают дополнительные напряжения, называемые монтажными напряжениями;

– свойство о температурных напряжениях – при изменении температуры окружающей среды в элементах статически неопределимых систем возникают температурные напряжения

где  – коэффициент линейного температурного расширения, град^–1.

Для решения статически неопределимых систем (с.н.с.), т.е. раскрытия их статической неопределимости в курсе сопротивления материалов используется метод сил. Рассмотрим его на примере решения жесткой балки, закрепленной с помощью двух стержней 1 и 2 (рисунок 1.18). Определим усилия, возникающие в этих стержнях, а также их площади сечения (А₁ и А₂ ).

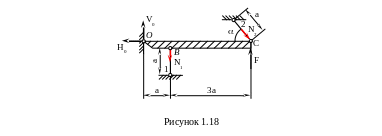
Исходные данные: [] = 160 МПа; F = 800 кН; А₁ : А₂ = 2 : 1;  = 60.

Решение

Раскрытие степени статической неопределимости системы выполняется путем рассмотрения следующих четырех сторон задачи.

I сторона задачи – статическая. Определяем степень статической неопределимости системы

Составляем уравнение статики достаточное и необходимое для решения задачи

после преобразований получим

II сторона задачи – геометрическая. Исходную схему с.н.с. изображаем в условно-деформированном состоянии согласно принципа возможных малых перемещений (рисунок 1.19).

Из геометрического рисунка находим зависимость между деформациями элементов статически неопределимой системы

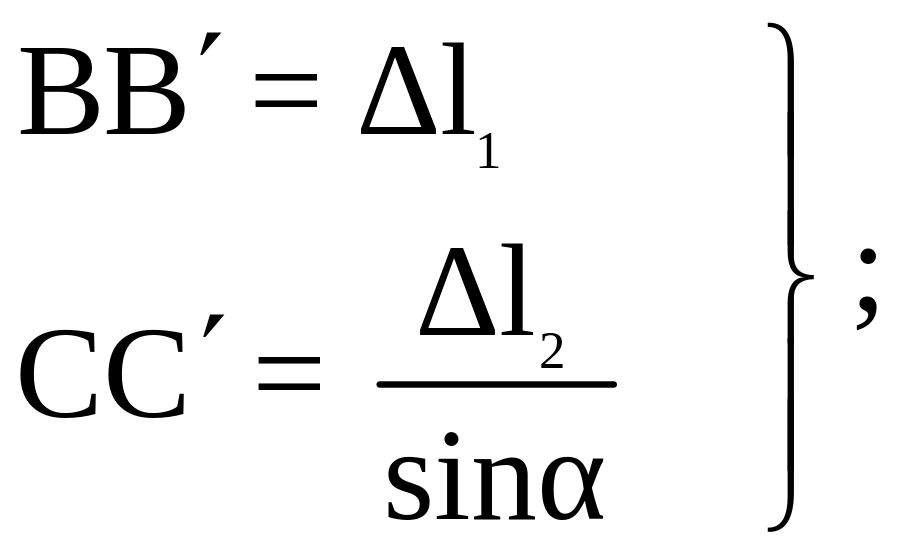
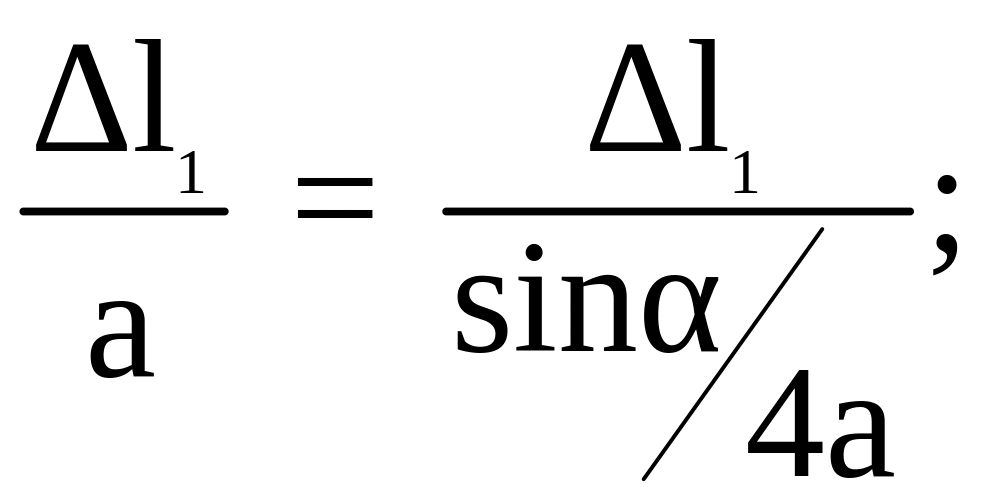
Полученное уравнение называется уравнением совместимости деформаций.

III сторона задачи – физическая. Чтобы связать уравнения (1.38) и (1.39), деформации элементов статически неопределимой системы представляем через усилия в них с использованием закона Гука в следующем виде:

IV сторона задачи – синтез.

Решаем совместно уравнения (1.38), (1.39) и (1.40). В итоге определяем искомые усилия в элементах статически неопределимой системы.

Подставляем (1.40) в (1.39), получим

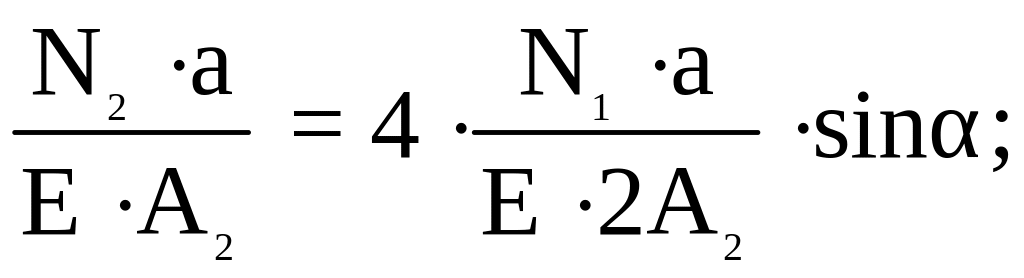
Подставляем (1.41) в (1.38), получим:

Подставляем (1.42) в (1.41), получим:

Производим подбор сечений стержней по принципу допускаемых напряжений, для этого устанавливаем более нагруженный стержень:

Выполняем проектировочный расчет по второму стержню.

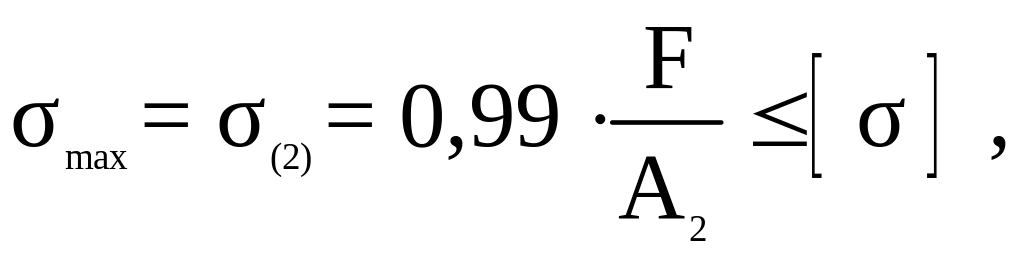
откуда

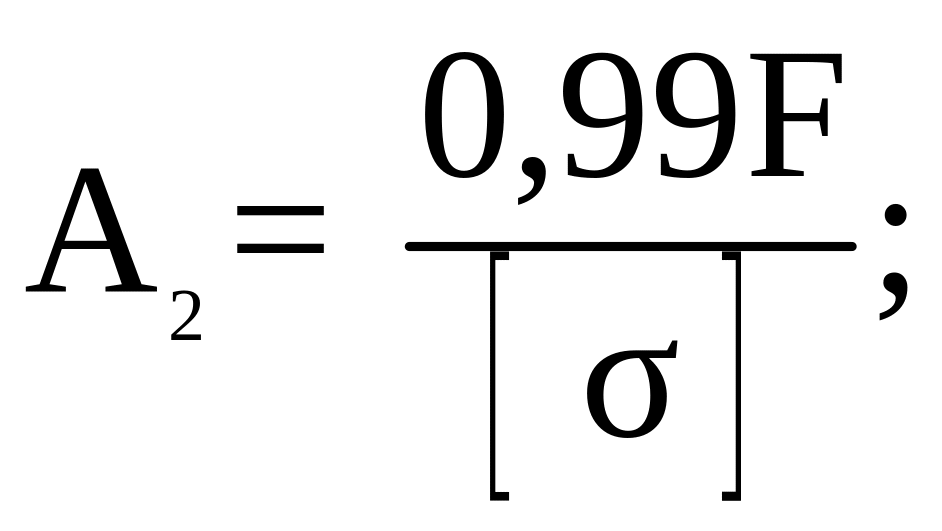
тогда

Выполняем подбор сечений стержней по принципу разрушающих нагрузок, для этого запишем уравнение равновесия (1.38) в виде уравнения появления текучести в элементах статически неопределимой системы

Учитывая, что получим

Разделим обе части уравнения на коэффициент запаса прочности - n, учитывая что

Подставляя эти выражения, получим

учитывая, что , получим

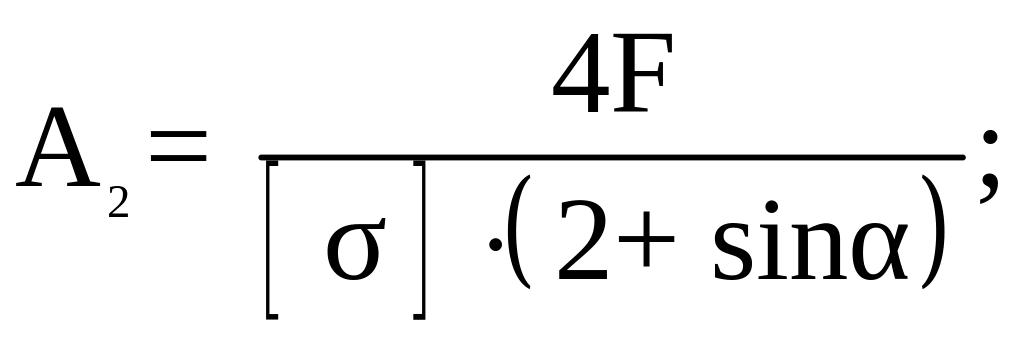
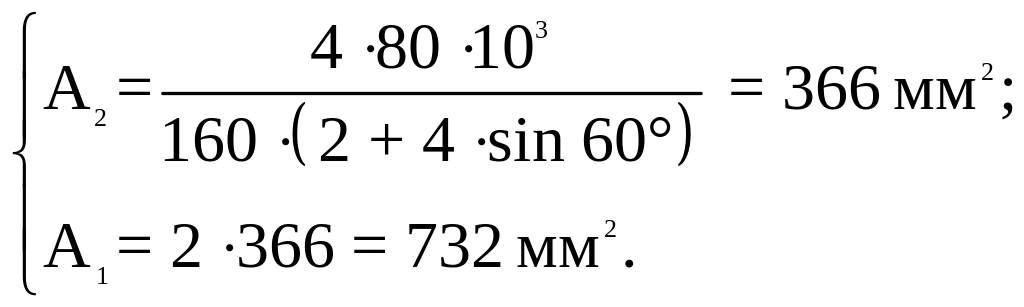
В итоге имеем:

- при расчете по принципу допускаемых напряжений:

- при расчете по принципу разрушающих нагрузок:

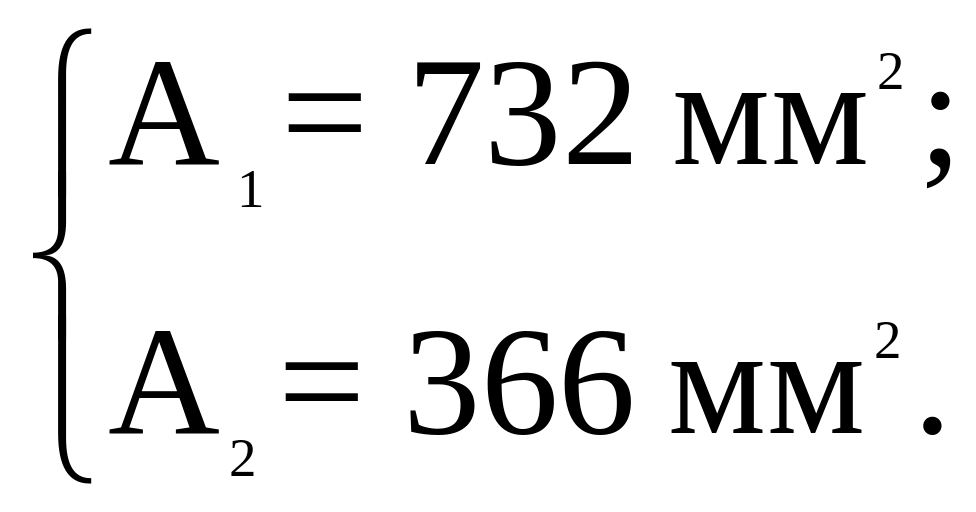
Таким образом, сравнивая два принципа расчета, видим, что расчет по принципу допускаемых напряжений является более надежным, а расчет по принципу разрушающих нагрузок – более экономичным.

При этом, расхождение в расчетах составляет

Окончательно принимаем площади сечения стержней по первому принципу расчета для обеспечения большей надежности

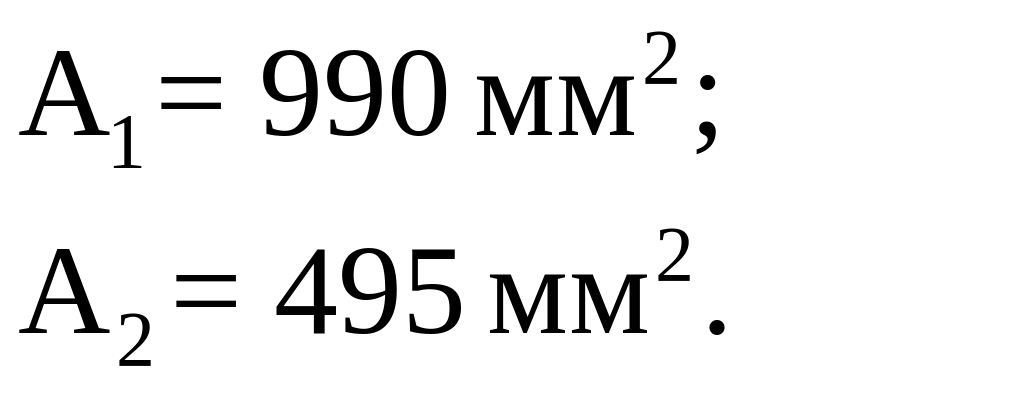
2 Основы теории напряженного состояния

2.1 Понятие напряженного состояния в точке. Виды напряженных состояний

При оценке прочности элементов конструкций, деталей машин и сооружений выполняется анализ наиболее опасных точек или частей этих конструкций. В окрестности исследуемой точки, (например, точки К) выделяется бесконечно малый параллелепипед (кубик) и выполняется анализ действующих по его граням (площадкам) напряжений (рисунок 2.1).

Рассмотрим более подробно кубик с действующими по его площадкам нормальными и касательными напряжениями (рисунок 2.2).

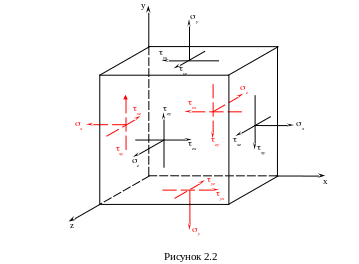
По шести площадкам кубика действуют 18 компонентов нормальных и касательных напряжений, которые попарно равны между собой, если имеют одинаковые индексы. Так, согласно закону парности касательных напряжений выполняются следующие равенства:

Для упрощения математической записи эти напряжений представляют в виде матрицы, которая называется тензором напряжений

Таким образом, под напряженным состоянием в точке понимается совокупность нормальных и касательных напряжений, действующих по различным площадкам и направлениям, проходящим через заданную точку. В общем случае напряженное состояние в точке характеризуется шестью компонентами напряжений – тремя нормальными и тремя касательными.

При изменении положения (ориентации) кубика в пространстве изменяются и действующие по его граням напряжения, при этом существует такое положение кубика, называемое главным, при котором все касательные напряжения  исчезают, т.е. обращаются в нуль. Тогда по главным площадкам будут действовать только главные нормальные напряжения – ₁, ₂, ₃.

Главные напряжения подчиняются следующему алгебраическому неравенству

Например, ₁=100 МПа > ₂ =10 МПа > ₃ = – 300 МПа.

Учитывая сказанное, тензор главных напряжений можно записать в следующем виде:

В зависимости от числа действующих главных напряжений все многообразие реальных напряженных состояний можно привести к трем основным видам – линейному, плоскому и объемному.

Линейное напряженное состояние (л.н.с.) или одноосное напряженное состояние это состояние, при котором из трех главных напряжений действует только одно главное напряжение. Линейное напряженное состояние возникает при деформации растяжения или сжатия, а также при деформации изгиба в крайних волокнах бруса (рисунок 2.3)

Изгиб бруса

Полный анализ линейного напряженного состояния был рассмотрен в разделе 1 “Растяжение-сжатие”.

Плоское напряженное состояние (п.н.с.) или двухосное напряженное состояние возникает, когда только одно главное напряжение обращается в нуль. Основные варианты п.н.с. могут быть записаны следующим образом:

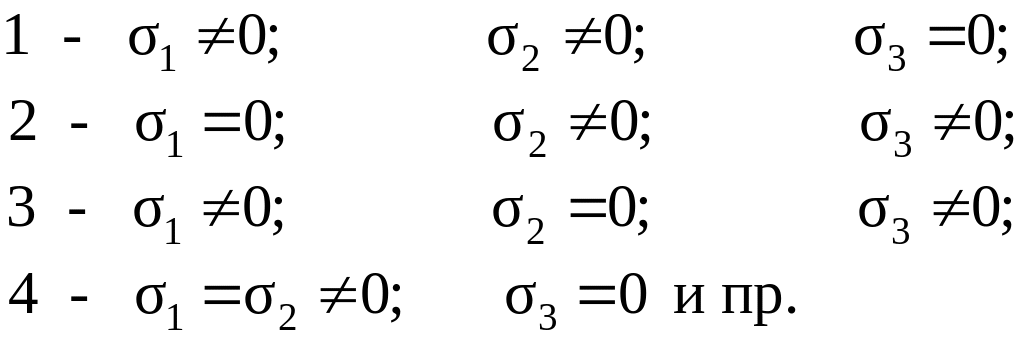
Плоское напряженное состояние возникает при деформации кручения, сдвига, среза, изгиба и при некоторых видах сложного сопротивления. В частности, плоское напряженное состояние имеет место в стенках сосудов небольшой толщины, нагруженных внутренним или наружным давлением p (рисунок 2.4)

Объемное напряженное состояние (о.н.с.) или трехосное напряженное состояние возникает, когда все три главных напряжения не равны нулю, т.е.

₁ ≠ 0; ₂ ≠ 0; ₃ ≠ 0.

Объемное напряженное состояние встречается в элементах тяжело нагруженных конструкций, в частности, в толстостенных сосудах, нагруженных давлением, а также в деталях, имеющих соединения с натягом (с посадкой).

2.2 Прямая и обратная задачи при плоском напряженном состоянии

В теории напряженного состояния часто решают задачи по определению напряжений на различных площадках (не главных или главных). Такие задачи называются, соответственно, прямой и обратной и для их решения можно использовать аналитический или графический способ.

Графический способ заключается в построении круговых диаграмм напряжений, называемых кругами Мора (предложены Отто Кристианом Мором). Рассмотрим более подробно решение прямой и обратной задач.

Прямая задача: Задана главная площадка с действующими на ней главными напряжениями ₁ и ₂, а также задан угол наклона  неглавной площадки ( > 0), для которой требуется определить нормальные и касательные напряжения

Аналитическое решение производится по следующим формулам:

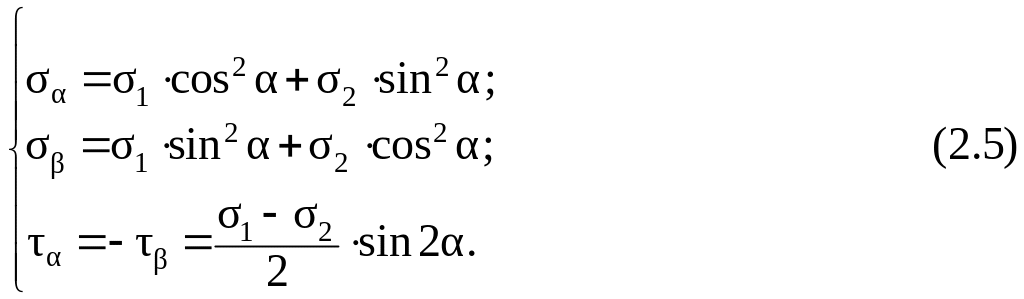
Зависимость (2.5) представляет собой уравнение окружности, записанное в параметрической форме, поэтому прямая задача имеет следующее графическое решение (рисунок 2.5).

K_ (_; _), K_ (_; _) – изображающие точки

Рисунок 2.5

Изображающие точки K_, K_ характеризуют искомые площадки с действующими по ним напряжениями.

Для установления направления искомых площадок и напряжений на круге находится положение полюса (П). Для этого необходимо из точек на круге с заданными напряжениями (₁, ₂) провести лучи по направлению этих напряжений; точка пересечения этих лучей и является полюсом. Полюс обладает тем свойством, что луч, соединяющий его с любой точкой на круге, указывает направление напряжения, соответствующего этой точке.

Проверка решения этой задачи производится по следующим условиям:

- сумма главных напряжений должна равняться сумме неглавных напряжений, действующих по граням заданного элемента напряженного состояния, т.е.

₁ + ₂ = _ + _ ;

- касательные напряжения _ и _ сходятся на той грани элемента, рядом с которой проходит алгебраически большее главное напряжение ₁, и напряжения _ и _ расходятся там, где проходит меньшее главное напряжение – ₂.

Обратная задача: Задана неглавная площадка и действующие на ней нормальные и касательные напряжения, т.е. _, _, _ = _. Требуется найти положение главной площадки, т.е. угол ₀ и величины главных нормальных ₁, ₂, и экстремальных касательных напряжений _max и _min.

Аналитическое решение производится по формулам:

Графическое решение обратной задачи выполняется в обратном порядке по сравнению с решением прямой задачи (рисунок 2.6).

Рисунок 2.6

В теории напряженного состояния чаще встречается обратная задача, т.к. это необходимо для установления экстремальных, опасных, напряжений, а также выполнения оценки прочности конструкции.

2.3 Обобщенный закон Гука. Удельная потенциальная энергия упругой деформации при сложном напряженном состоянии

Ранее была получена зависимость, выражающая закон Гука для линейного напряженного состояния (см. главу 1 “Растяжение-сжатие”).

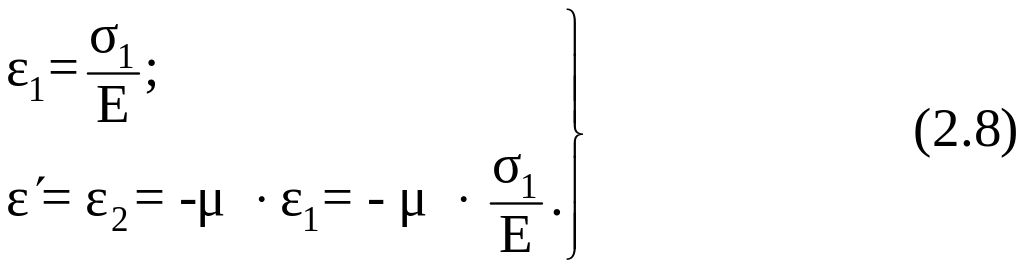
Получим аналогичные зависимости для плоского или объемного напряженных состояний, которые называются сложным напряженным состоянием.

Найдем главную деформацию по направлению ₁ (рисунок 2.7) как сумму продольной деформации от действия напряжения ₁, и двух поперечных деформаций от напряжений ₂, и ₃

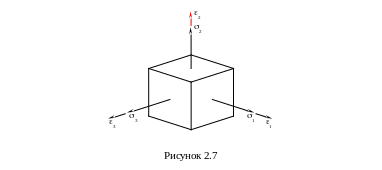
Подставим (2.8) в (2.9), получим

Аналогично получим две другие главные деформации ₂ и ₃. Тогда зависимости обобщенного закона Гука можно представить в следующем виде:

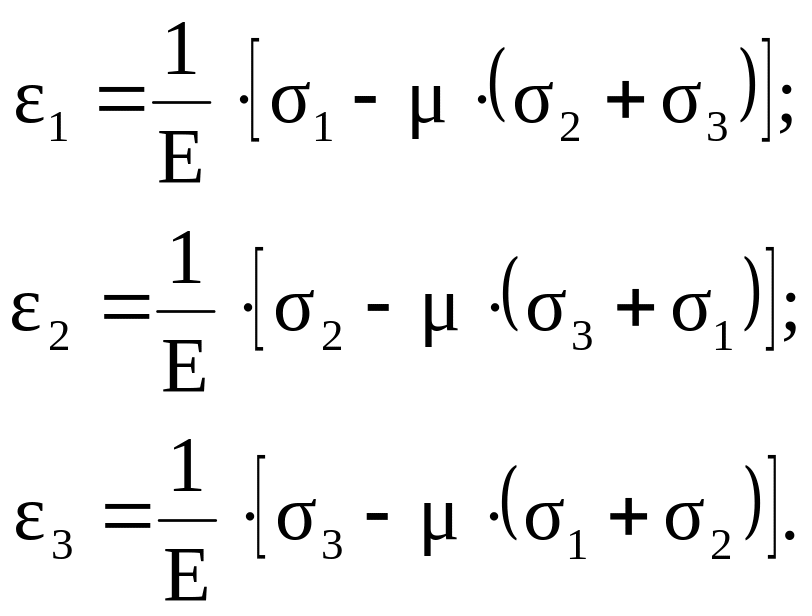(2.10)

Удельная потенциальная энергия упругой деформации (УПЭУД) для случая линейного напряженного состояния (см. раздел 1 “Растяжение-сжатие”) была представлена в следующем виде

Получим аналогичную зависимость для УПЭУД в случае плоского и объемного напряженны состояний. Для этого, аналогично (2.11), составим сумму произведений главных напряжений на соответствующие главные деформации

С учетом (2.11) преобразуем (2.12), получим УПЭУД для сложного напряженного состояния

Потенциальная энергия упругой деформации затрачивается как на изменение формы, так и на изменение объема деформируемого тела, т. е.

где u_Ф, u_V – удельная потенциальная энергия изменения формы и изменения объема, соответственно, определяются по формулам

Используя зависимости удельной потенциальной энергии упругой деформации и её составляющих, можно разработать способы оценки прочности элементов конструкций и деталей машин. В курсе сопротивления материалов в качестве такого способа широко применяются так называемые гипотезы прочности (или теории пластичности и разрушения).

2.4 Теории прочности (гипотезы пластичности и разрушения)

В случае линейного напряженного состояния оценка прочности выполняется по следующей схеме

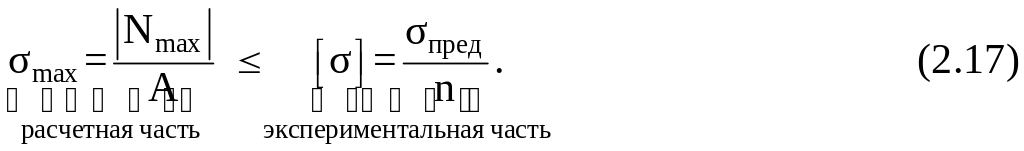
Здесь предельное напряжение определяется на основании результатов испытания на одноосное растяжение

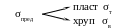
Для плоского и объемного напряженных состояний эта схема неприменима, т. к. сложно установить расчетную величину максимального напряжения, а с другой стороны, весьма трудоемко экспериментально определить предельное напряжение материала. Поэтому при решении такой задачи предлагается заменить сложное напряженное состояние линейным, но эквивалентным по прочности заданному напряженному состоянию (рисунок 2.8)

Тогда для эквивалентного н.с. оценку прочности выполняют по следующему условию

где [σ] – допускаемое напряжение, принимается как для обычного линейного напряженного состояния.

Величину эквивалентного напряжения определяют с помощью различных теорий (гипотез разрушения и пластичности), в которых за критерий разрушения или пластичности принимаются разнообразные параметры напряженно-деформированного состояния конструкции. Рассмотрим некоторые из этих теорий.

I теория прочности – теория (критерий, гипотеза) максимальных нормальных напряжений _max (Галилей / Рэнкин). I теория предполагает, что разрушение конструкции происходит, если одно из наибольших по модулю главных напряжений достигает предельного значения. Условие прочности по этой теории можно представить в таком виде

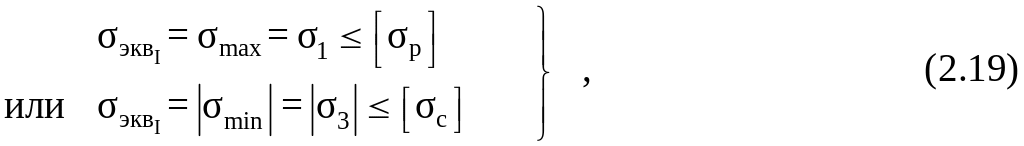
где [σ_р]; [σ_с] – допускаемое напряжение материала конструкции на растяжение или сжатие, соответственно,.

Эта теория применяется для очень хрупких материалов (например, фарфор, стекло, керамика и т.п.).

II теория прочности – теория максимальных относительных деформаций ε_max (Мариотт / Сен-Венан). Используя зависимость обобщенного закона Гука можно записать, что

В этом случае условие прочности имеет вид

Теория применяется только для хрупких материалов (чугун, бетон, кирпич).

III теория прочности – теория максимальных касательных напряжений _max (Кулон / Треска, Гест).Условие прочности имеет вид

Теория применяется только для пластичных материалов (сталь, титан, алюминиевые сплавы и пр.).

IV теория прочности – критерий максимальных потенциальных энергий изменения формы u_Фmax (энергетическая) (Мизес, Губер, Генки).

Условие прочности имеет вид

Теория также применима для пластичных материалов.

V теория прочности – эмпирическая теория (О.Мор). Теория основана на экспериментальных (эмпирических) данных и по упрощенной схеме сводится к следующему: для данного материала производятся лабораторные испытания на растяжение и сжатие, определяются показатели прочности и строятся два круга напряжений (рисунок 2.9). К полученным кругам проводятся две касательные, которые ограничивают область обеспечения прочности. Для оценки прочности заданного напряженного состояния по двум главным напряжениям строятся круг напряжений, и выясняют его расположение в области обеспечения прочности. Если этот круг не выходит за пределы этой области, то прочность данного напряженного состояния обеспечена, если, выходит – нарушена (рисунок 2.9).

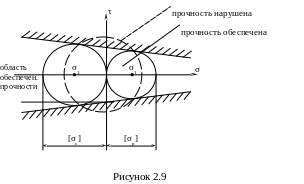
По V теории прочности условие прочности можно записать в следующем виде

где m – безразмерный коэффициент, определяется следующим образом

V теория прочности применима как для пластичных, так и для хрупких материалов.

Рассмотренные теории взаимосвязаны между собой, т.е. дают сопоставимые результаты при использовании для соответствующих материалов.

3 Кручение

3.1 Понятие о кручении валов

К ручение – это вид деформации, при котором в сечениях бруса, называемого валом, возникает только один внутренний силовой фактор - крутящий момент (рисунок 3.1).

Кручение создается парой внешних моментов, которые называются вращающими моментами М_вр.

Иногда в расчетах вращающий момент задается через величину мощности Р, л.с. или кВт, и число оборотов вала n, об/мин. В этом случае передаваемый валом вращающий момент, Нм, находится по формуле

При кручении вала его сечения скручиваются, что характеризуется угловым перемещением, которое называется углом закручивания – φ [рад], [град].

На основании экспериментальных данных между крутящим моментом и углом закручивания получают зависимость, которая называется диаграммой кручения (рисунок 3.2).

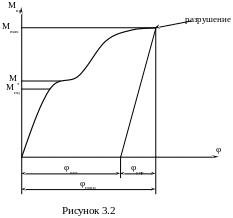
Практика показывает, что на особенности кручения существенное влияние оказывает форма поперечного сечения вала. Наиболее широко применяются валы круглого профиля, поэтому более подробно рассмотрим теорию кручения таких валов.

3.2 Теория кручения валов круглого профиля. Чистый сдвиг. Напряжения и деформации при кручении круглых валов

В теории кручения круглых валов принимаются такие допущения:

1 Справедлива гипотеза плоских сечений – сечения, плоские до деформации, остаются плоскими и после деформации.

2 Считается, что при скручивании вала его радиусы остаются прямолинейными, т.е. не искривляются (рисунок 3.3)

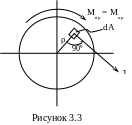
Получим зависимость для касательных напряжений при кручении круглого вала, для этого рассмотрим четыре стороны задачи.

Статическая сторона задачи. Согласно интегральным уравнениям равновесия имеем следующую зависимость между касательными напряжениями τ и крутящим моментом

где ρ –расстояние (радиус) от центра сечения до произвольной точки, м.

Геометрическая сторона задачи. Анализируя деформацию элемента на поверхности скручиваемого вала, видим, что его грани смещаются, т.е. элемент подвергается сдвигу (рисунок 3.4).

Элемент, находящийся только под действием касательных напряжений, подвергается чистому сдвигу и называется площадкой чистого сдвига (п.ч.с.) (рисунок 3.5), т.е. при кручении каждая точка вала находится в напряженном состоянии чистого сдвига.

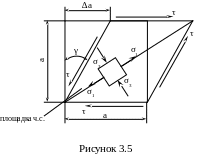
Из рисунка (3.5) установим количественный параметр деформации чистого сдвига – угол сдвига (учитывая, что это бесконечно малая величина) по формуле

Решая обратную задачу, видим, что для площадки чистого сдвига главные площадки повернуты на 45º, а главные напряжения равны по величине касательному напряжению (рисунок 3.6).

Выделим из вала бесконечно малый элемент длиной dz (рисунок 3.7).

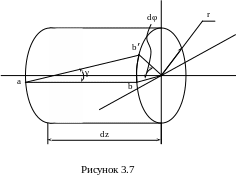
Получим зависимость для угла сдвига γ из соотношения

где – погонный или относительный угол закручивания, рад/м.

Тогда для произвольной точки вала, расположенной на радиусе ρ, получим

Физическая сторона задачи. При кручении и сдвиге закон Гука (по аналогии с растяжением-сжатием) имеет вид

где G – модуль упругости второго рода или модуль сдвига (для стали принимается равным G_сталь = 8∙10⁴ МПа) определяется из соотношения

Синтез. Решая совместно (3.1), (3.4), (3.5), получим формулу для касательных напряжений в произвольной точки вала при кручении

Максимальные напряжения возникают на поверхности вала, т.е. при максимальном радиусе (при ρ = ρ_max = r = d/2)

где – полярный момент сопротивления, м³, характеризует способность вала заданных размеров и формы выдерживать соответствующий крутящий момент.

Таким образом, при кручении максимальное напряжение возникает на поверхности вала, а минимальное ближе к его центру, т.е. эпюра касательных напряжений имеет следующий вид (рисунок 3.8).

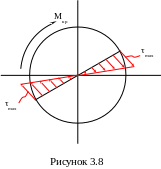
Учитывая это можно заключить, что при кручении наиболее рациональными являются пустотелые валы или валы кольцевого сечения

Рассматривая четыре стороны задачи с точки зрения деформаций, можно получить зависимость для угла закручивания вала

где – жесткость сечения вала, МПаžм⁴;

– жесткость вала, МПаžм³.

3.3 Расчет на прочность и жесткость валов круглого и некруглого профиля

При кручении круглых валов должны выполняться условия прочности и жесткости.

Условие прочности для валов круглого профиля имеет вид

где [τ] - допускаемое касательное напряжение, МПа, определяется через основное допускаемое напряжение по одной из следующих теорий прочности:

- по третьей теории прочности

[τ]_III =0,5ž[s];

- по четвертой теории прочности

[τ]_IV =0,6ž[s].

Условие жесткости для валов круглого профиля представляют в виде

где [θ] -допустимый относительный угол закручивания, рад/м, выбирается по нормативным документам.

При расчёте на прочность и жесткость валов некруглого профиля необходимо в условиях (3.10) и (3.11) заменить соответствующие геометрические характеристики следующим образом:

где α, β - безразмерные коэффициенты, зависящие от соотношения размеров сечения b, h, выбираются из справочной литературы.

По условиям (3.10) и (3.11) выполняются три вида расчетов вала (аналогично деформации растяжения-сжатия): проверочный, проектировочный и определение максимальной грузоподъемности вала.

ПРИЛОЖЕНИЕ А

Пример решения расчетно-проектировочной работы

Задача 1. Расчет бруса на осевое растяжение-сжатие

Задание

Вычертить схему нагружения бруса с обозначением численных значений приложенных нагрузок. Построить эпюру продольной силы. Подсчитать сторону «а» квадратного сечения, вычертить эскиз бруса. Высчитать нормальное напряжение на всех участках, построить эпюру нормального напряжения по длине бруса. Определить абсолютную деформацию бруса.

Исходные данные: [σ] = 100 МПа;

E = 210 ГПа;

F₁ = 40 кН;

F₂ = 20 кН;

F₃ = 60 кН;

b = 0,04 м;

c = 0,08 м;

d = 0,06 м;