Задание 1. Определители. Вычислить определители.

Вариант 1. 1.1 1.2 Вариант 2. 1.1 1.2

Вариант 3. 1.1 1.2 Вариант 4. 1.1 1.2

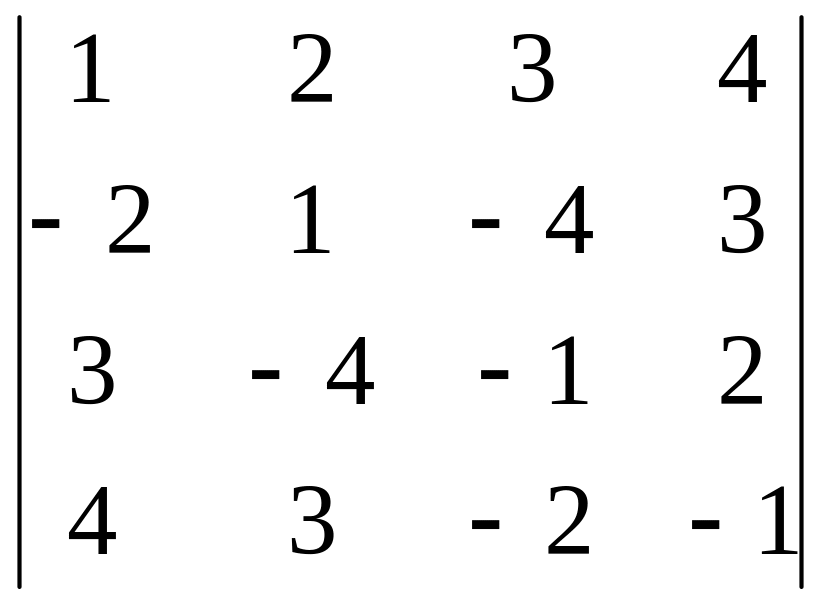Вариант 5. 1.1 1.2 Вариант 6. 1.1 1.2

Вариант 7. 1.1 1.2 Вариант 8. 1.1 1. 2

Вариант 9. 1.1 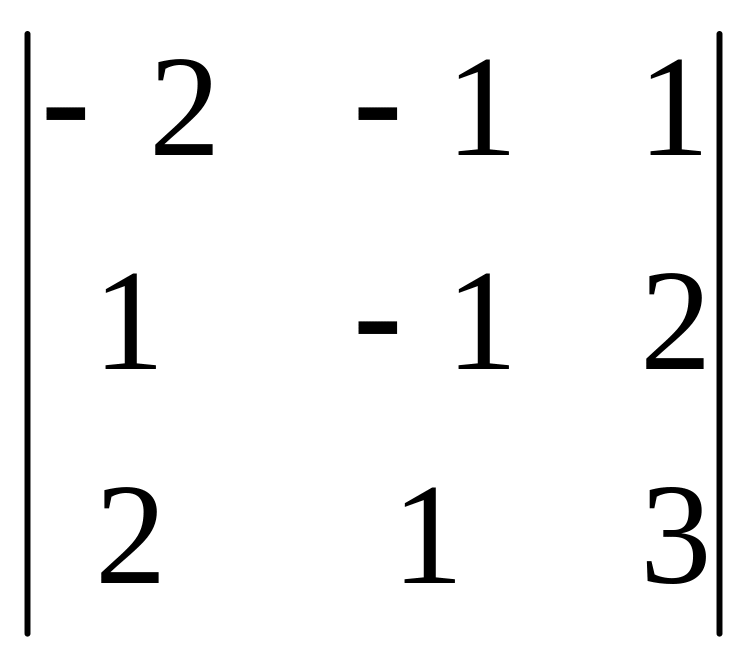1.2 Вариант 10. 1.1 1.2

Задание 2. Матрицы.

Вычислить 3А – 2В + АВ

В.1 , В.2 ,

В.3 , В.4 ,

В.5 , В.6 ,

В.7 , В.8 ,

В.9 , В.10 ,

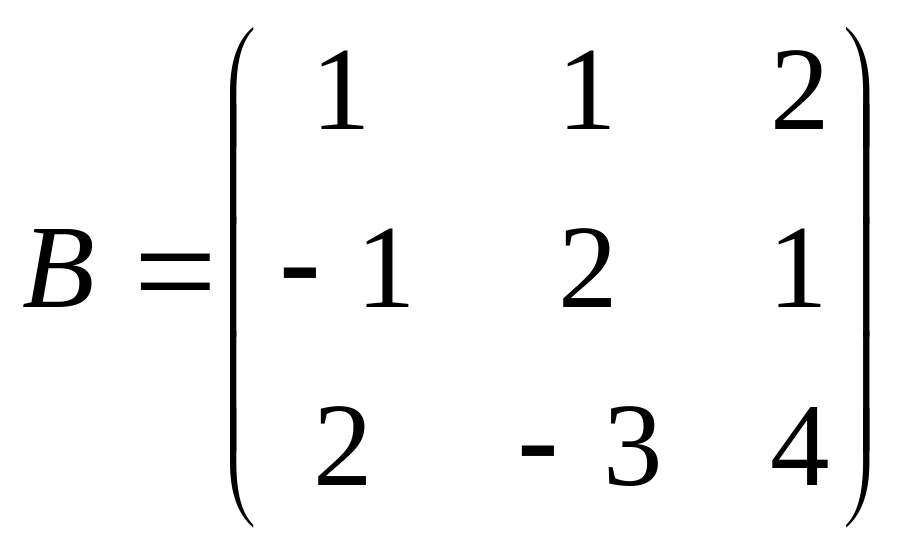
Задание 3. Системы уравнений.

1. Решить систему методом Крамера и проверить методом Гаусса.

2. Решить систему с помощью обратной матрицы.

В-1 3.1 3.2 В-2 3.1 3.2

В-3 3.1 3.2 В-4 3.1 3.2

В-5 3.1 3.2 В-6 3.1 3.2

В-7 3.1 3.2 В-8 3.1 3.2

В-9 3.1 3.2 В-10 3.1 3.2

Задание 4. Базис n-мерного векторного пространства. Разложение вектора по базису.

Даны векторы {а ; а ; а }, {b ; b ; b }, {c ; c ; c } и {d ; d ; d } в некотором базисе. Показать, что векторы , , образуют базис и найти координаты вектора в этом базисе.

1. = {1; 2; 3}, = {-1; 3; 2}, = {7; -3; 5} и = {6; 10; 17}

2. ={4; 7; 8}, ={9; 1; 3}, ={2; -4; 1} и ={1; -13; -13}

3. ={8; 2; 3}, ={4; 6; 10}, ={3; -2; 1} и ={7; 4; 11}

4. ={10; 3; 1}, ={1; 4; 2}, ={3; 9; 2} и ={19; 30; 7}

5. ={7; 2; 1}, ={4; 3; 5}, ={3; 4; -2} и ={2; -5; -13}

6. ={2; 7; 3}, ={3; 1; 8}, ={2; -7; 4} и ={16; 14; 27}

7. ={1; -2; 3}, ={4; 7; 2}, ={6; 4; 2} и ={14; 18; 6}

8. ={2; 4; 1}, ={1; 3; 6}, ={5; 3; 1} и ={24; 20; 6}

9. ={1; 7; 3}, ={3; 4; 2}, ={4; 8; 5} и ={7; 32; 14}

10. ={1; 4; 3}, ={6; 8; 5}, ={3; 1; 4} и ={21; 18; 33}

Задание 5. Прямая на плоскости

В АВС даны координаты вершин.

1.Построить чертеж. 2. Найти периметр треугольника. 3. Составить уравнения сторон треугольника.

4. Составить уравнение прямой ВN // АС. 5. Составить уравнение медианы СД.

6. Уравнение высоты АЕ, найти ее длину. 7. Найти углы треугольника. 8. Найти координаты центра тяжести.

Вариант	1	2	3	4	5	6	7	8	9	10
А	(1; -1)	(0; -1)	(1; -2)	(2; -2)	(0; 1)	(3; -2)	(3; -3)	(-1; 1)	(3; -3)	(2; 2)
В	(4; 3)	(3; 3)	(4; 2)	(5; 2)	(3; 5)	(6; 2)	(6; 1)	(2; 5)	(6; 1)	(5; 6)
С	(5; 1)	(4; 1)	(5; 0)	(6; 0)	(4; -3)	(7; 0)	(7; -1)	(3; 3)	(7; -1)	(6; 4)

Задание 6. Прямая и плоскость.

Даны координаты вершин пирамиды А А А А . Найти:

1. длину ребра А А ; 2) угол между ребрами А А и А А ;

3. площадь грани А А А ; 5) объем пирамиды;

4. уравнение прямой А А ; 6) уравнение плоскости А А А ;

7. угол между ребром А А и гранью А А А ;

8. уравнение высоты и ее длину, опущенной из вершины А на грань А А А ;

9. сделать чертеж.

Вариант	А	А	А	А
1	(7; 7; 3)	(6; 5; 8)	(3; 5; 8)	(8; 4; 1)
2	(4; 2; 5)	(0; 7; 2)	(0; 2; 7)	(1; 5; 0)
3	(4; 4; 10)	(4; 10; 2)	(2; 8; 4)	(9; 6; 4)
4	(8; 6; 4)	(10; 5; 5)	(5; 6; 8)	(8; 10; 7)
5	(10; 6;6)	(-2; 8; 2)	(6; 8; 9)	(7; 10; 3)
6	(4; 6; 5)	(6; 9; 6)	(2; 10; 10)	(7; 5; 9)
7	(7; 2; 2)	(5; 7; 7)	(5; 3; 1)	(2; 3; 7)
8	(3; 5; 4)	(8; 7; 4)	(5; 10; 4)	(4; 7; 8)
9	(6; 6; 5)	(4; 9; 5)	(4; 6; 11)	(6; 9; 3)
10	(1; 8; 2)	(5; 2; 6)	(5; 7; 4)	(4; 10; 9)

Задание 7. КРИВЫЕ ВТОРОГО ПОРЯДКА.

1.Найти координаты вершины и фокусов параболы, составить уравнения оси и директрисы параболы

Вариант 1. а/ у²-6у-12х-15=0, б/ х²-4х-16у+52=0. Вариант 2. а/ х²-2х-12у+13=0, б/ у²-4у-12х+16=0.

Вариант 3. а/ у²+6у-8х+1=0, б/ х²+6х-12у+21=0 Вариант 4. а/ х²+2х-20у-79=0, б/ у²-4у+8х-12=0.

Вариант 5. а/ у²-4у-16х+52=0, б/ х²+8х-28у+44=0. Вариант 6. а/ х²+8х+16у +48=0, б/ у²-4у-24х+28=0.

Вариант 7. а/ х²-6х-12у-15=0, б/ у²-4у-16х+52=0. Вариант 8. а/ у²-2у-12х+13=0, б/ х²-4х-12у+16=0.

Вариант 9. а/ у²+6х-8у+1=0, б/ х²+6у-12х+21=0. Вариант 10. а/ у²+2у-20х-79=0, б/ х²-4х+8у-12=0.