3 Практическое занятие № 3. Анализ электромагнитного состояния трансформатора и электромеханического состояния двигателей

Задача 1. Расчет трехфазного трансформатора.

Необходимо построить внешнюю характеристику трансформатора ТМ-100/6. Исходные данные к задаче: номинальная мощность S_Н = 100 кВ∙А, номинальное напряжение на зажимах первичной обмотки трансформатора U_1Н = 6 кВ, напряжение холостого хода на зажимах вторичной обмотки трансформатора U_2Н = 0,36 кВ, напряжение короткого замыкания U_К% = 6% от U_1Н, мощность короткого замыкания Р_К = 0,9 кВт, коэффициент мощности нагрузки cosφ = 0,75. Соединение обмоток трансформатора Y/Y («звезда/звезда») (рисунок 3.1).

а)

б)

Рисунок 2.4 – Модель трёхфазной электрической цепи переменного тока к задаче 2: а- соединение «звезда», б- соединение «треугольник»

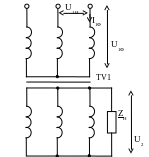
Рисунок 3.1 – Схема трехфазного трансформатора

Решение.

Для построения зависимости напряжения на вторичной обмотке трансформатора от коэффициента его загрузки - внешней характеристики, находим потери напряжения во вторичной обмотке трансформатора для равного 0 и 1:

где , – соответственно активная и реактивная составляющие напряжения короткого замыкания.

Напряжение на зажимах вторичной обмотки трансформатора определяем по формуле

.

Номинальный ток первичной обмотки трансформатора

А,

активное сопротивление короткого замыкания

Ом,

полное сопротивление короткого замыкания

Ом.

Для соединения «звезда/звезда» ,

;

;

Для = 0 (точка 1 на рисунке 3.2)

для = 1 (точка 2 на рисунке 3.2)

400

В

1

2

300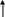

200

U₂

100

0 0,2 0,4 0,6 0,8 1

β

Рисунок 3.2 – Внешняя характеристика трансформатора

Задача 2. Расчет трехфазного асинхронного двигателя с короткозамкнутым ротором

Построить механическую характеристику асинхронного двигателя по характерным точкам. Исходные данные к задаче: номинальная мощность трехфазного асинхронного двигателя Р_Н =10 кВт, номинальное напряжение U_H = 380 В, номинальное число оборотов ротора n_H = 1420 мин^-1, номинальный КПД η_Н = 84 %, номинальный коэффициент мощности cosφ_Н = 0,85, кратность пускового тока I_П/I_Н = 6,5, перегрузочная способность двигателя m_К =1,8, число пар полюсов р = 2.

Решение.

Асинхронный двигатель М малой мощности с короткозамкнутой обмоткой ротора подключается к сети с помощью магнитного пускателя, который состоит из контактора синусоидального тока КМ и встроенных в него тепловых реле КК (рисунок 3.3).

При включенном автоматическом выключателе QF пуск двигателя осуществляется нажатием кнопки SB2. При этом срабатывает контактор КМ. Его главные контакты, замыкаясь, присоединяют обмотки фаз статора к сети. Одновременно в цепи управления замыкаются вспомогательные контакты КМ, блокирующие кнопку SB2 так, что при возврате ее в исходное положение рабочее состояние контактора не изменяется. Нажатием кнопки SB1 двигатель отключается от сети. При этом цепь тока управления контактором размыкается. Автоматический выключатель QF защищает двигатель от токов короткого замыкания (I >), а тепловые реле КК – от длительных перегрузок.

Потребляемая двигателем мощность:

кВт.

Номинальный и максимальный моменты:

Н∙м;

Н∙м.

А В С

QF

I >

FU1

KK

KK

KK

SB2

KM

KM

M

FU2

SB1

KM

Рисунок 3.3 – Схема пуска асинхронного двигателя

Номинальный и пусковой токи:

А;

А.

Синхронная частота вращения поля ротора:

мин^-1.

Номинальное скольжение

.

Формула для определения критического скольжения может быть получена в результате подстановки в уравнение номинального скольжения:

.

Зависимость электромагнитного момента асинхронного двигателя от скольжения - механическая характеристика строится по уравнению:

.

Расчетные данные сводим в таблицу 3.1.

Таблица 3.1 – Результаты расчета механической характеристики

S	М, Н∙м
0	0
0,053 (sн)	67,3 (Мн)
0,175 (sк)	121,0 (Мн)
1,0	41,2

По данным таблицы строим механическую характеристику (рисунок 3.4).

Н м

M_K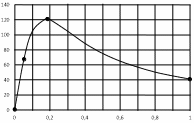

M

M_H

S_K

S_H

S

Рисунок 3.4 – Механическая характеристика асинхронного двигателя

Задача 3. Расчет двигателя постоянного тока параллельного возбуждения

Для двигателя М постоянного тока параллельного возбуждения (см. рисунок 3.5) требуется построить естественную механическую характеристику n = f(M) и механическую характеристику при пуске с пусковым реостатом R_П с током, равным 2 номинальных тока двигателя I_Н.

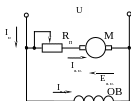
Рисунок 3.5 – Схема включения двигателя параллельного возбуждения

Исходные данные к задаче: номинальная мощность кВт, номинальное напряжение В, номинальная частота вращения якоря мин^-1, номинальный КПД η = 92%, сопротивление обмотки якоря и дополнительных полюсов в нагретом состоянии Ом, сопротивление обмотки возбуждения Ом.

Решение.

Номинальная мощность, потребляемая двигателем из сети,

Вт.

Номинальный ток, потребляемый двигателем из сети,

А.

Ток в обмотке якоря в номинальном режиме работы (по первому закону Кирхгофа, рисунок 3.5)

А.

Противо ЭДС, индуцируемая в обмотке якоря при номинальной частоте его вращения,

В.

Номинальная электромагнитная мощность

Вт.

Номинальный вращающий электромагнитный момент

Н∙м.

Частота вращения якоря в режиме идеального холостого хода

мин^-1.

Пусковой ток якоря при введении в цепь якоря пускового реостата

А.

Сопротивление пускового реостата

Ом.

При будут постоянными ток возбуждения и магнитный поток , из чего следует

,

Н∙м.

Механическая характеристика двигателя представляет собой зависимость частоты вращения вала от момента n = f(M) и может быть построена по двум точкам. Первая точка соответствует режиму холостого хода n = n₀ (M=0), вторая – для естественной характеристики n = n_н (M = M_н), для искусственной характеристики при пуске n = 0 (M = M_п). Механические характеристики двигателя представлены на рисунке 3.6.

Рисунок 3.6 – Механические характеристики двигателя постоянного тока параллельного возбуждения: 1 – естественная; 2 – искусственная при пуске

Практическое занятие №4. Разработка схем и расчет элементов выпрямителей, усилителей и устройств на логических элементах

Задача 1. Расчёт однофазного неуправляемого выпрямителя

Разработать схему, осуществить расчёт и выбор элементов мостового выпрямителя на полупроводниковых диодах с индуктивно-емкостным LC-фильтром.

Исходные данные к задаче: напряжение сети U₁ = 220 В, номинальное напряжение нагрузки U_d = 50 В, номинальный ток нагрузки I_d = 0,6 А, частота питающего напряжения f = 50 Гц.

Решение.

Схема однофазного мостового выпрямителя с LC-фильтром приведена на рисунке 4.1.

TV1

Рисунок 4.1 – Схема однофазного мостового выпрямителя с индуктивно-емкостным LC-фильтром

Решение.

Номинальная мощность нагрузки:

Вт.

Сопротивление нагрузки

Ом.

Для однофазного мостового выпрямителя среднее значение прямого тока через вентиль (выпрямительный диод) определяется как

А.

Обратное максимальное напряжение на вентиле равно:

В.

Выбираем вентили (выпрямительные диоды) 1N4934 (приложение А) c параметрами:

– максимальный прямой ток I_{пр max}=1A > I_а=0,3A;

– максимально допустимое обратное напряжение U_{обр max} = 100 В > >U_аобрmax = 78,5 В;

– максимальное напряжение в открытом состоянии U_{пр max}=1,1В.

Для однофазного мостового выпрямителя действующее значение вторичного напряжения равно:

В.

Расчётная мощность трансформатора определяется как

В∙А.

Выбираем трансформатор (приложение Б) ТПП 271-127/220-50:

В∙А > В∙А.

При последовательном соединении вторичных обмоток А, Б, В, Г получаем U₂ = 9,95 + 10 + 20 + 20 = 59,95 В.

Тогда коэффициент трансформации

Коэффициент пульсации на выходе однофазного мостового выпрямителя К_п =0,67.

Требуемый коэффициент пульсации К_н = 0,007.

Тогда коэффициент сглаживания фильтра равен:

Для LC–фильтра

Гн∙Ф,

где m– число пульс выпрямленного напряжения за период.

Зададимся мкФ из стандартного ряда Е24 (приложение В). Тогда

Гн.

Параметры фильтра мкФ, Гн удовлетворяют условиям эффективной работы:

; .

; .

Модель в среде Multisim однофазного неуправляемого мостового выпрямителя с фильтром приведена на рисунке 4.2.

Показания измерительных приборов соответствуют расчётным значениям.

Рисунок 4.2 – Модель мостового выпрямителя с индуктивно-емкостным фильтром

Задача 2. Расчёт инвертирующего усилителя низкой частоты на основе операционного усилителя.

На основе операционного усилителя КР140УД11 разработать схему инвертирующего усилителя низкой частоты с коэффициентом усиления К_U = 20 и минимальным входным напряжением U_вхmin = 10 мВ. Определить максимальное входное напряжение синусоидального сигнала U_{вх max}, при котором не будет значительных искажений выходного сигнала.

Решение.

Параметры операционного усилителя КР140УД11:

– номинальное напряжение питания U_{пит ном}=±15 В;

– коэффициент усиления K_{u ОУ}=30000;

– максимально допустимое выходное напряжение U_{вых max}=12 В;

– разность входных токов ΔI_вх=0,2 мкА;

– входное сопротивление R_вх=0,4 МОм;

– минимальное сопротивление нагрузки R_{Н min}=2 кОм.

С

R₂

хема инвертирующего усилителя низкой частоты приведена на рисунке 4.3.

DA1

R₁

U_вх

R₃

Рисунок 4.3 – Схема инвертирующего усилителя на ОУ КР140УД11

Сопротивление R₁ должно удовлетворять условию:

R₁ << кОм.

Принимаем из стандартного ряда Е24 (приложение В) R₁ = 5,1 кОм.

Сопротивление обратной связи

R₂ =K_U·R₁= 20·5,1·10³ = 102 кОм.

Принимаем R₂ =100 кОм.

Для уравнивания входных токов ОУ по обоим входам в цепь неинвертирующего входа включают резистор R₃:

кОм.

Принимаем R₃ =4,7 кОм.

Амплитуда выходного сигнала не может быть больше максимального выходного напряжения (для данного типа ОУ U_{вых max}=12 В). Поэтому действующее значение максимального входного синусоидального сигнала составит:

В.

Модель инвертирующего усилителя на ОУ в среде Multisim приведена на рисунке 4.4.

Рисунок 4.4 – Модель инвертирующего усилителя на ОУ

В результате моделирования получаем коэффициент усиления:

,

что близко к заданному коэффициенту усиления K_U=20.

Задача 3. Разработка устройства на логических элементах

Разработать устройство управления механизмом на логических элементах серии К1533, работа которого контролируется по 3 параметрам Х1, Х2, Х3, принимающих значения логического 0 и 1 и описывается функцией . Определить состояние функции при всех возможных значениях входных сигналов.

Решение.

Для реализации функции (рисунок 4.5) требуются четыре логических элемента: 2 элемента НЕ – DD1 микросхема К1533ЛН1 (приложение Г) содержит 6 элементов НЕ в одном корпусе; 1 элемент 2ИЛИ-НЕ – DD2 микросхема К1533ЛЕ1 (приложение Г) содержит 4 элемента 2ИЛИ-НЕ в одном корпусе; 1 элемент 2И-НЕ – DD3 микросхема К1533ЛА3 (приложение Г) содержит 4 элемента 2И-НЕ в одном корпусе. Т.к. в данной серии отсутствует необходимый элемент 2ИЛИ, он был заменен на элемент 2ИЛИ-НЕ, выходной сигнал от которого был дополнительно инвертирован с помощью второго элемента НЕ.

Для определения состояния функции Y (таблица 4.1) для различных комбинаций входных переменных Х1, Х2, Х3 (следует воспользоваться таблицами истинности логических элементов (приложение Д).

На рисунке 4.5 представлены состояния входов/выходов всех логических элементов для выделенного в таблице 4.1 состояния входных переменных.

0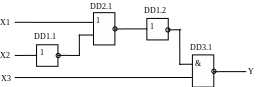

0

1

1

0

1

1

Рисунок 4.5 – Реализация логической функции

Таблица 4.1 – Таблица истинности логической функции Y

X1	X2	X3	Y
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

На рисунке 4.6 представлена модель в среде Multisim реализованного устройства управления механизмом, подтверждающая состояние функции Y=1 и промежуточных значений при состояниях входных переменных X1=0, X2=1, X3=1.

Рисунок 4.6 – Модель устройства управления механизмом на основе логических элементах