5.2. Второй фундаментальный закон механики – закон баланса момента количества движения (кинетического момента)

Скорость изменения кинетического момента относительно неподвижной точки равна главному моменту внешних воздействий плюс скорость подвода кинетического момента:

. (5.11)

Кинетический момент (момент импульса) одной точки ; тела, состоящего из материальных точек:

; (5.12)

тела, занимающего какую–либо область в пространстве с непрерывно распределенной массой (континуального тела) (рис. 5.4):

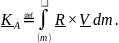(5.13)

Скорость подвода момента количества движения в тело определяется как

, где – присоединяющаяся к телу за время со скоростью масса.

Главным моментом внешних воздействий называется (см. рис. 2.1) сумма , где – сосредоточенные, массовые, контактные силы соответственно, а – моменты.

Третий закон Ньютона. Из двух законов следует третий закон Ньютона для точек:

.

Запишем законы для каждой из точек и для системы из двух точек:

, , ;

, ,

.

Складывая уравнения для каждой из точек и вычитая уравнения для системы из двух точек, получим:

; .

Теорема об изменении кинетического момента. В механике Ньютона, где тела состоят из материальных точек, а силы взаимодействия между ними центральны и подчинены третьему закону, закон баланса кинетического момента доказывается как теорема об изменении кинетического момента.

Дифференцируя по времени момент (5.12) с помощью второго закона Ньютона для точки получим:

Последняя двойная сумма разбивается на равные нулю суммы пар слагаемых: и окончательно получим теорему: .

5.2.1. Зависимость кинетического момента от выбора опорной точки. Кинетический момент твердого тела. Тензор инерции

Хотя закон баланса кинетического момента сформулирован в инерциальной системе отсчета относительно неподвижной точки, сам кинетический момент может вычисляться и относительно подвижной точки.

Рассмотрим любое (не обязательно твердое) тело и две произвольные, может быть подвижные, точки M и N (рис. 5.5,a).

Заменив = , получим:

. (5.14)

Рассмотрим движение твердого тела в любой (необязательно инерциальной) системе отсчета. Найдем кинетический момент относительно какой–либо точки В, принадлежащей телу (т. е. движущейся вместе с телом) (рис. 5.5,б).

Подставим в определение (5.12) основную формулу кинематики твердого тела , взяв за полюс точку В:

.

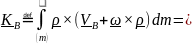Первое слагаемое в соответствии с определением центра масс

имеет вид .

Во втором слагаемом раскроем двойное векторное произведение:

.

Независящий от переменных интегрирования вектор угловой скорости вынесем из интеграла со знаком скалярного умножения, представив , где, напомним, единичный тензор, представимый в ортонормированном базисе в виде . Тогда

.

Описывающий распределение массы вокруг точки В интеграл называется тензором инерции тела в точке В (или относительно точки В):

(5.15)

Таким образом, кинетический момент твердого тела относительно принадлежащей ему точки, называемый собственным кинетическим моментом, имеет вид:

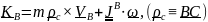. (5.16)

Формула упрощается, если в качестве полюса В выбрать центр масс; тогда и

, (5.17)

где тензор инерции тела относительно центра масс называется центральным. Если тело вращается вокруг неподвижной точки В, то

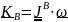. (5.18)

Для произвольного движения твердого тела наиболее удобно использовать в формуле (5.14) собственный кинетический момент относительно центра масс:

. (5.19)