3. Решение уравнений четвертой степени.
Чтобы найти все корни уравнения четвертой степени, делят обе его части на коэффициент при старшей степени x, что не меняет корней уравнения и затем в уравнении
(7)
делают замену
неизвестного
(используют схему Горнера). В результате
получается уравнение
(8)
Если
,
,
,
корни уравнения (8), то
– корни уравнения (7). Здесь i=1,2,3,4
корни уравнения (8) можно получить
следующим образом.
Способ Феррари.
Составляется кубическое уравнение
(9)
(кубическая
резольвента уравнения (8)) и берется один
из его корней
.
Затем составляются два квадратных
уравнения
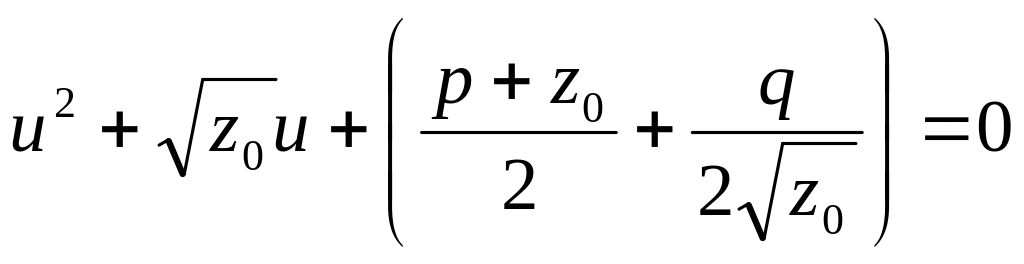, (10)
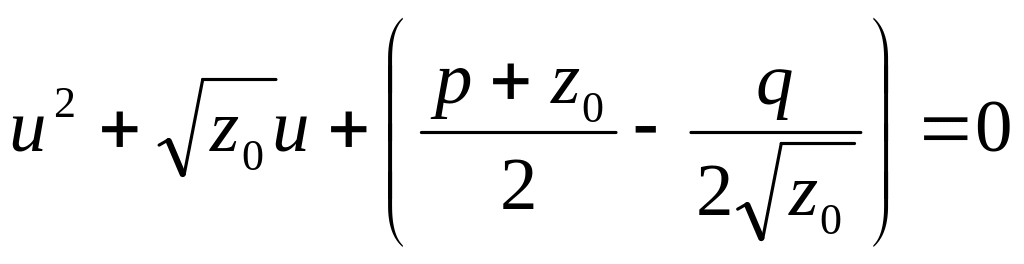. (11)
Корни уравнений (10) и (11) служат корнями уравнения (8).
Способ Эйлера.
Составляем уравнение
(9) и находим его корни
,
,
.
Корни уравнения (8) находим по формулам
, 
,
, 
.
где знаки
выбираются так, чтобы выполнялось
равенство
.
Пример.
Решить уравнение
.
Решение.
Пусть x=y+1, тогда данное уравнение примет вид
.
Кубической резольвентой этого уравнения является
.
Один из ее корней
.
Запишем уравнения (10) и (11) соответственно
,
.
Их корни
,
.
Находим корни данного уравнения
,
.
Ответ:
.
Домашнее задание.
Решить уравнение третьей степени .
Решить уравнение четвертой степени
Симметрические многочлены от X и y
1. Примеры симметрических многочленов.
Многочлен от x и y называется симметрическим, если он не изменяется при замене x на y, а y на x.
Например, многочлен
– симметрический, а
– не является симметрическим многочленом.
Симметрические многочлены x+y
и xy
называют элементарными
симметрическими
многочленами от x
и y.
Для них используют специальное обозначение
и
.
Кроме
и
часто встречаются так называемые
степенные суммы, то есть многочлены
,
,…,
,…
Принято обозначать многочлен
через
.
Таким образом
2. Основная теорема о симметрических многочленах от двух переменных
Если взять любой многочлен от и и подставить в него вместо и их выражения и , то получится симметрический многочлен от x и y.
Теорема.
Любой симметрический многочлен от x и y, можно представить в виде многочлена от и .
3. Выражение степенных сумм через и .
Покажем, что каждую
степенную сумму
можно представить в виде многочлена от
и
.
С этой целью мы умножим обе части
равенства
на
.
Получим:
.
Таким образом
. (1)
Из этой формулы и вытекает справедливость нашего утверждения. С помощью формулы (1) можно построить следующую таблицу.
Выражение степенных сумм через и . |
|
Метод вычисления
степенных сумм основанный на применении
формулы (1), обладает одним недостатком:
чтобы найти выражение для
,
надо предварительно вычислить все
предыдущие суммы. Формула
(2)
была открыта в 1779 году английским математиком Эдуардом Варингом. Она называется формулой Варинга и лишена вышеуказанного недостатка.
Все слагаемые в правой части (2), могут быть получены одним и тем же методом: надо в выражении
числу m
придавать последовательно значения
0,1,2,… вплоть до наибольшего значения
m,
при котором показатель k-2m
еще не отрицателен (то есть до наибольшего
целого числа, не превосходящего
).