Разложение правильной рациональной дроби на простейшие, знаменатель которой разложен на попарно простые линейные множители.

Пусть дана правильная дробь

; при , i,j=1,2,…,n.

В этом случае справедлива формула Лагранжа:

,

где .

Интерполирование

Постановка задачи.

Пусть в точках таких, что . Известны значения функции , то есть на отрезке [a,b] задана табличная (сеточная) функция :

Таблица 1

x			…
y			…

Функция f(x) называется интерполирующей или интерполяционной для на отрезке [a,b], если ее значения в заданных точках , называемых узлами интерполяции, совпадают с заданными значениями функции , то есть с соответственно.

Будем считать, что интерполяционная функция f(x) есть многочлен степени n-1, тогда задача интерполяции формулируется так: для функции заданной таблицей 1 найти многочлен такой, чтобы выполнялась совокупность условий интерполяции

, (2)

найти многочлен это значит, учитывая его каноническую форму

, (3)

найти его n коэффициентов . Обозначим через и рассмотрим рациональную дробь . Она правильная, так как степень многочлена в числителе меньше степени многочлена стоящего в знаменателе. Мы можем применить формулу Лагранжа для разложения дроби на простейшие. Получим интерполяционную формулу Лагранжа:

.

Пример.

Найти многочлен наименьшей степени по данной таблице его значений:

x	-1	0	1	2	3
y	6	5	0	3	2

Решение.

;

;

; ; ; ; .

Пример для самостоятельного решения.

Найти многочлен наименьшей степени по данной таблице его значений:

x	1	2	3	4	6
y	5	6	1	-4	10

Отыскание корней многочленов

1. Решение уравнений второй степени

Корни квадратного уравнения

с любыми действительными или комплексными коэффициентами находятся по формуле

Для корней «приведенного» квадратного уравнения справедлива формула

Пример.

Решить уравнение

.

Решение.

, .

2. Решение уравнений третьей степени.

Чтобы найти все корни уравнения третьей степени

,

удобно разделить обе части этого уравнения на , в результате получим уравнение вида

, (1)

имеющее те же корни, что и исходное уравнение, а затем сделать замену неизвестного . Эту замену проще всего осуществить разложив многочлен по степеням с помощью схемы Горнера и заменив затем через y. В результате указанной замены получится уравнение вида

(2)

Корни этого уравнения находятся по формуле

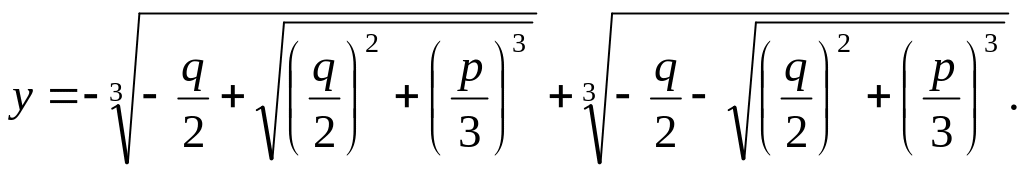(3)

это формула Кардано.

Применяя эту формулу, нужно для каждого из трех значений корня

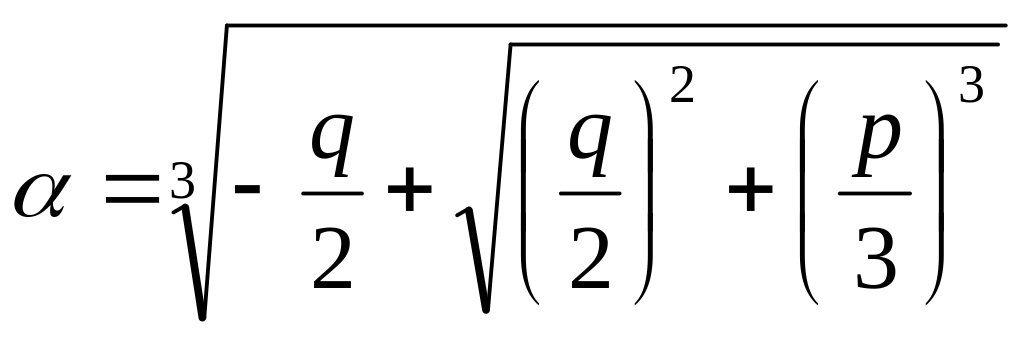(4)

брать то значение корня

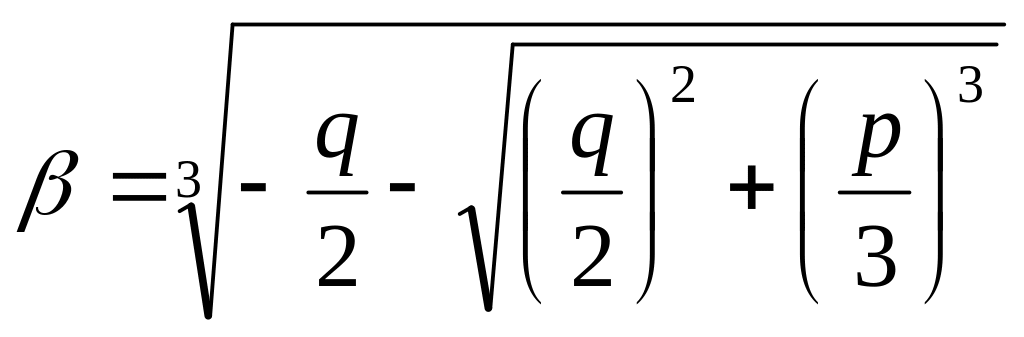, (5)

для которого выполняется условие (такое значение корня всегда существует). Если , , – корни уравнения (2), то

, , – корни уравнения (1).

Пример.

Решить уравнение

.

Решение.

Разложим многочлен стоящий в левой части уравнения, по степеням x+1.

,

,

.

Пусть , тогда уравнение имеет вид

Находим корни последнего уравнения

Значениями корня являются числа

, , .

Соответствующие им значения второго корня

, , .

Отсюда

, , .

Корни исходного уравнения: , , .

Ответ: { , , }.

Замечание.

Корни уравнения (2) можно находить по формулам

(6)

где в качестве берется любое из значений корня (4), а в качестве – то значение корня (5), для которого .

Пример для самостоятельного решения.

Решить уравнение

.