
- •Определение полиномов и операции с ними. Кольцо полиномов. Стандартная запись полиномов.
- •Отношение делимости в кольце полиномов от одной переменной. Свойства.
- •Деление с остатком в кольце полиномов от одной переменной. Теорема о делении с остатком.
- •Наибольший общий делитель и наименьшее общее кратное полиномов. Алгоритм Евклида. Линейное выражение нод. Взаимно простые полиномы и их свойства.
- •8. Полиномиальные отображения. Корни полинома. Деление полинома на линейный двучлен. Схема Горнера. Теорема Безу.
- •9. Теоремы о рациональных корнях полиномов над полем рациональных чисел.
- •Неприводимые полиномы. Примеры, свойства. Единственность разложения на неприводимые множители.
- •Каноническое разложение на неприводимые множители. Нахождение нод и нок полиномов.
- •Функциональное и алгебраическое равенства полиномов.
- •10. Производная полинома. Определение и свойство производной полинома.
- •11. Кратные множители и кратные корни полинома.
- •20. Степени полиномов от нескольких переменных. Однородные многочлены.
- •21. Лексикографическое упорядочение полиномов от нескольких переменных.
- •22. Функциональное и алгебраическое равенства полиномов от нескольких переменных.
- •23. Симметрические полиномы. Элементарные симметрические полиномы. Теорема Виета.
- •24. Элементарные симметрические полиномы. Алгебраическая независимость.
- •25. Основная теорема о симметрических полиномах и ее приложение к вычислению выражений от корней многочлена.
- •26. Дискриминант полиномов.
- •27. Результант полиномов.
- •28. Применение результанта для решения систем алгебраических уравнений.
Определение полиномов и операции с ними. Кольцо полиномов. Стандартная запись полиномов.
Определение
полиномов: Пусть
К
–
коммутативное кольцо с единицей, х
– некоторая группа, не принадлежащая
этому кольцу. Выражение вида (формальная
запись)
а0х0+а1х1+а2х2+…+аnxn,
где
 ,
называется полиномом (многочленом) от
одной переменной (от буквы х)
над кольцом К.
,
называется полиномом (многочленом) от
одной переменной (от буквы х)
над кольцом К.
 – свободный
член (слагаемое), где а0
–
нулевой коэффициент.
– свободный
член (слагаемое), где а0
–
нулевой коэффициент.
 – старший
коэффициент, n
– степень полинома n=deg f(x)=deg (f(x)).
0x0-
считается,
что deg
0x0=
– старший
коэффициент, n
– степень полинома n=deg f(x)=deg (f(x)).
0x0-
считается,
что deg
0x0= .
Если а0х0,а0
.
Если а0х0,а0 0,
то
степень полинома равна нулю. Множество
всех полиномов от одной буквы – К[x].
0,
то
степень полинома равна нулю. Множество
всех полиномов от одной буквы – К[x].
Определение:
Два
полинома
 называются равными, если:
называются равными, если:
m=n
 (ai=bi)
(ai=bi)m>n
 (ai=bi)
,
(ai=bi)
,
 (bi=0)
(bi=0)m>n
 (ai=bi),
(ai=bi), (ai=0)
(ai=0)
Определение:
Пусть
 ,
тогда их суммой называется полином
,
тогда их суммой называется полином
 .
.
Свойство: Множество <K[x], +> является коммутативной группой:
б.а.о. задана. f(x), g(x)
 K[x]
K[x] (f(x)+g(x))
K[x]
f(x)+g(x)=
(f(x)+g(x))
K[x]
f(x)+g(x)= ai
,bi
K
(ai+bi)
ai
,bi
K
(ai+bi)
операция ассоциативная
 f(x),
g(x),
h(x):
(f(x)+g(x)+h(x))=((f(x)+g(x))+h(x))
f(x),
g(x),
h(x):
(f(x)+g(x)+h(x))=((f(x)+g(x))+h(x))
 :(f(x)+g(x)+h(x))=
:(f(x)+g(x)+h(x))=
 .
((f(x)+g(x))+h(x))=
.
((f(x)+g(x))+h(x))=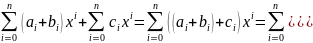
 (f(x)+0(x)=0(x)+f(x))=f(x)
0(x)=0x0=
(f(x)+0(x)=0(x)+f(x))=f(x)
0(x)=0x0=
 f(x)+(-f(x))=(-f(x))+f(x)=0(x);
f(x)+(-f(x))=(-f(x))+f(x)=0(x);
<K[x],+> - коммутативная? f(x) g(x) f(x)+g(x)=g(x)+f(x)
f(x)+g(x)= =g(x)+f(x)
=g(x)+f(x)
Определение:
Пусть
 ,
тогда их произведением называется
полином
,
тогда их произведением называется
полином
 ,
,
 .
.
d0=a0b0
d1=a0b1+a1b0
d2=a0b2+a2b0+a1b1
………………………
dn+m=anbm
Свойство: Пусть <K[x], *> - полугруппа. Условия:
Б.а.о. f(x), g(x) K[x] f(x)*g(x) K[x] di K.
Ассоциативность.
Свойство: Пусть <K[x], +, *> - коммутативное кольцо с единицей.
<K[x], +>- коммутативная группа
<K[x], *> - полугруппа
Дистрибутивность: f(x)*(g(x)+h(x))=f(x)*g(x)+f(x)*h(x)
(g(x)+h(x))*f(x) =g(x)*f(x) +h(x)*f(x)
Определение: <K[x], +, *> называется кольцом полиномов от одной переменной (буквы) над кольцом К.
Замечание: В дальнейшем выражение вида а0х0 будем отождествлять с а0 (на операцию это не повлияет).
Определение: а, в К называются делителями 0, если а 0, в 0, а*в=0 ( в числовых множествах такого нет).
Свойство:
Если
в кольце К
нет делителя нуля, то deg(f(x))*g(x))=deg
f(x)+deg
g(x)
f(x)= ,
g(x)=
,
g(x)= an
0,
bm
0
f(x)*g(x)=
an
0,
bm
0
f(x)*g(x)= dn+m=an*bm
dn+m=an*bm .
.
Свойство: Если К без делителей нуля, то и кольцо K[x] без делителей нуля.
Отношение делимости в кольце полиномов от одной переменной. Свойства.
Пусть везде К – коммутативное кольцо с единицей без делителя нуля.
Определение:
f(x),
g(x)
K[x],
g(x)
0.
Говорят, что f(x)
делится на g(x)
(кратен g(x)),
если
 .
.
Свойство: 1. Если f(x)=g(x)*h(x),то 1.
2.
f(x)
Доказательство:



3.
(f1(x)u1(x)+f2(x)u2(x)) g(x)
g(x)
4. .
.
Свойство:
Если
f(x) ,
где с
–
обратимый элемент кольца К.
,
где с
–
обратимый элемент кольца К.
Свойство: Обратимые элементы кольца K[x] – это обратимые элементы кольца К, только и только они.
Доказательство:
f(x) – обратимый в K[x]





a0 – обратимый элемент в кольце К.
Необходимость:
если
 -
обратимый
элемент, т.е.
-
обратимый
элемент, т.е.


