Варианты к типовому расчету

Задание №3

Прибор состоит из m узлов, которые могут заменять друг друга. Для нормальной работы прибора достаточно функционирования хотя бы одного узла. При выходе из строя трех узлов прибор не работает. Среднее время безотказной работы одного узла t часов, среднее время ремонта распределено по показательному закону и равно в среднем S часов. Поток отказов простейший. В начальный момент времени все узлы исправны. Найти среднюю производительность прибора, если с выходом из строя каждого узла прибор теряет (100/m) % своей номинальной производительности.

№ вар.	m	T	S	№ вар.	m	t	S
1	3	22	8	16	3	12	4
2	4	12	2	17	4	16	8
3	5	10	5	18	5	45	9
4	3	55	5	19	3	20	5
5	4	15	3	20	4	22	8
6	5	18	2	21	5	24	6
7	3	18	3	22	3	8	2
8	4	10	5	23	4	14	3
9	5	15	5	24	5	30	6
10	3	35	7	25	3	18	4
11	4	10	2	26	4	12	3
12	5	12	6	27	5	16	6
13	3	15	4	28	3	45	3
14	4	18	2	29	4	20	8
15	5	20	4	30	5	22	11

Пример 4 Техническое устройство состоит из двух узлов. Каждый из узлов в любой момент времени может выйти из строя и сразу же начинает ремонтироваться соответственно первой и второй ремонтными бригадами. Среднее время безотказной работы первого узла – 10 суток, второго узла – 15 суток, среднее время ремонта первого узла – 24 часа, второго узла –

12 часов. Потоки отказов и ремонтов простейшие. В начальный момент времени оба узла исправны. Найти среднюю стоимость ремонта узла за 1000 часов работы устройства, если 1 час ремонта первого узла стоит 5, а второго –

3 условных единицы.

Решение. Возможные состояния системы: – оба узла исправны; – первый узел ремонтируется, второй – исправный; – второй узел ремонтируется, первый узел исправен; – ремонтируются оба узла.

λ₁=1/35

λ₂=1/35

λ₄=1/15

μ₂= 2

μ₁=1

μ₄= 1

μ₃=2

λ₃=1/1

Рис. 2.4. Размеченный граф состояний системы

Размеченный граф состояний системы изображен на рис. 2.4.

Из состояния в состояние систему переводит поток отказов первого узла с интенсивностью отказов в сутки; из состояния в состояние – поток отказов второго узла с интенсивностью отказов в сутки. Из состояния в состояние систему переводит поток восстановлений первого узла с интенсивностью восстановление в сутки, из состояния в состояние – поток восстановления второго узла с интенсивностью восстановления в сутки. Аналогично можно получить

.

Все состояния системы существенные, сообщающиеся. Следовательно, предельные вероятности состояний существуют. Для предельных вероятностей состояний имеем систему линейных однородных алгебраических уравнений

(7)

Кроме того, выполняется нормировочное условие:

(8)

В системе (7) каждое из уравнений есть линейная комбинация остальных уравнений системы. Например, сложив второе и третье уравнения и вычтя первое, получим четвертое уравнение.

Система (7) равносильна системе уравнений

Решение этой системы имеет вид

где

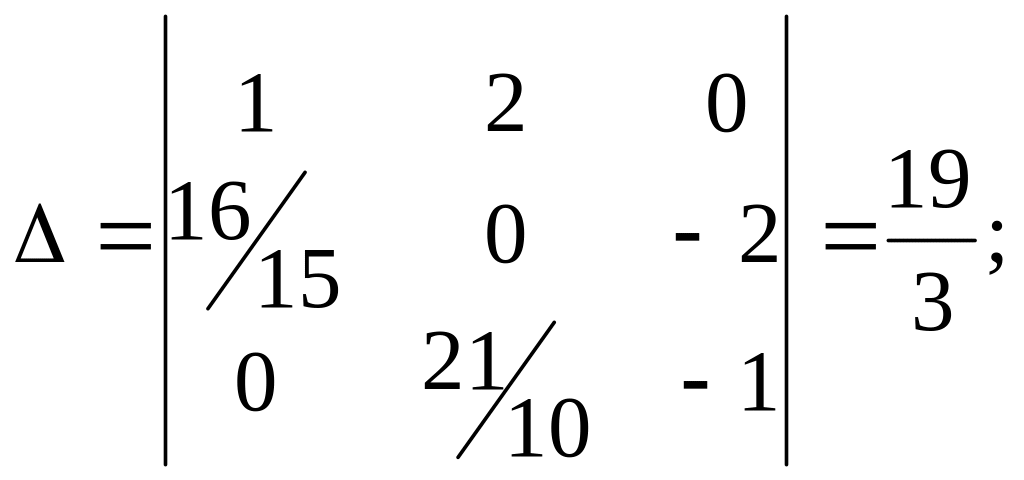
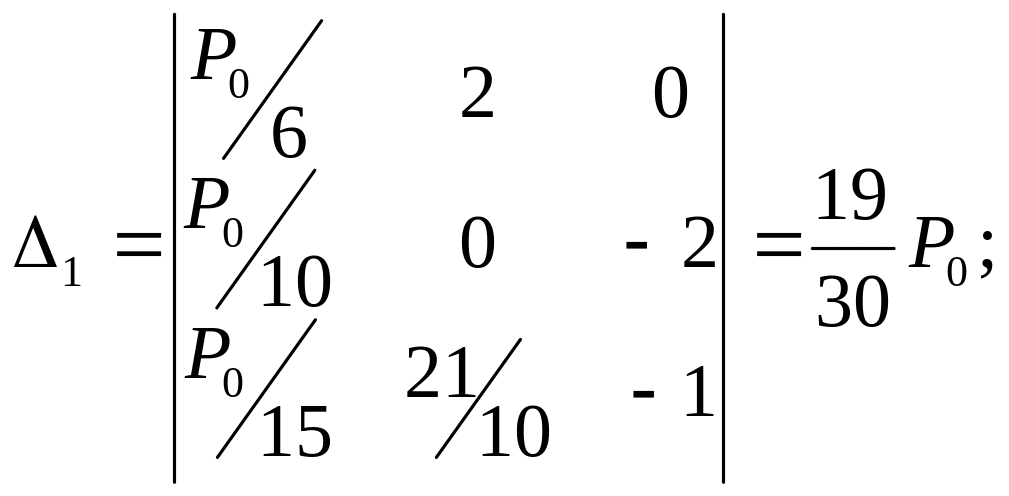
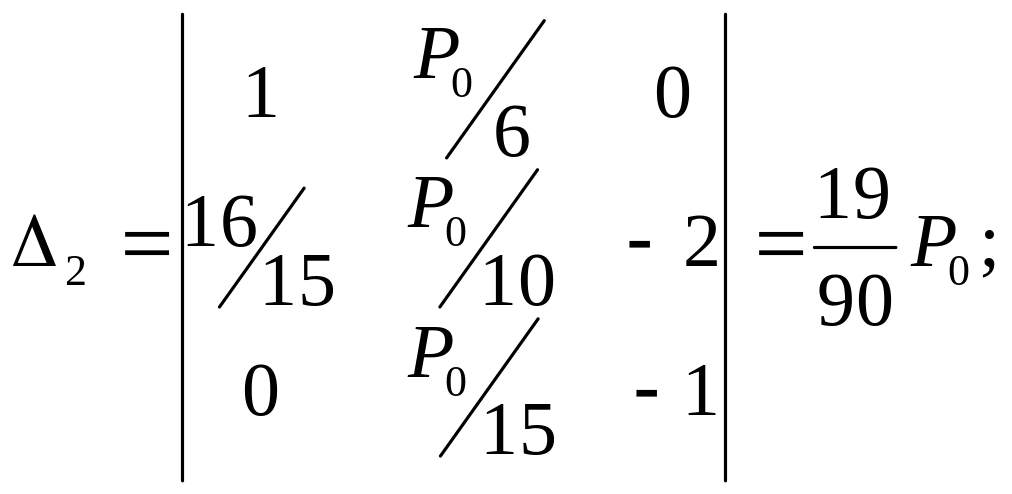
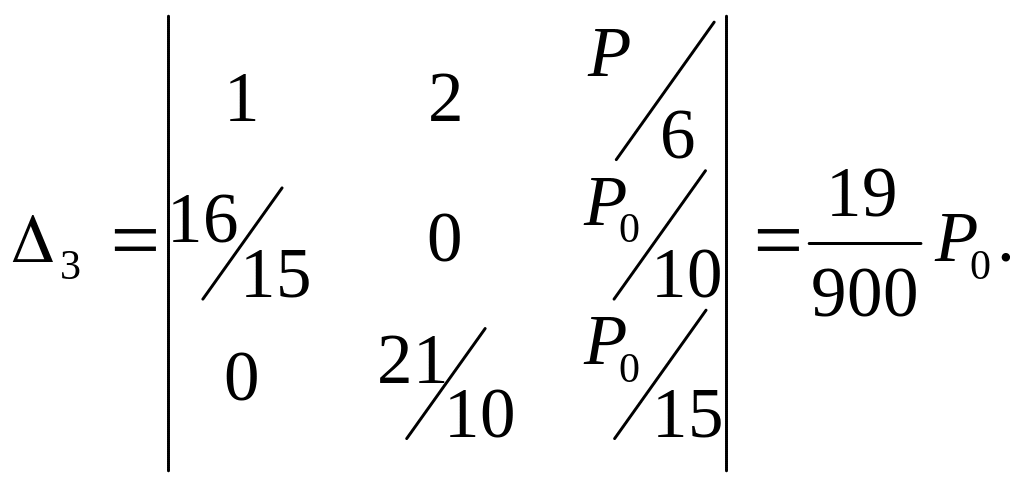
Следовательно,

Подставив полученные вероятности в нормировочное условие (8), получим

Следовательно,

Выводы. Средняя стоимость П ремонта узлов за 1000 часов работы устройства определяется следующим образом:

(условных единиц).