Лабораторная работа № 8
Система № 2 — «парк приема – горка» (система № 2 таблица 1).
|
n |
|
(n-1) |
|
(n-2) |
|
(n-3) |
|
(n-4) |
|
|
|
х0 |
|
х1 |
|
х2 |
|
х3 |
|
х4 |
|
х5 |
|
х6 |
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
|
х0 – горка не занята;
х1 – на горке один состав, очереди нет;
х2 – на горке один состав, 1 состав в очереди;
х3 – на горке один состав, 2 состава в очереди;
х4 – на горке один состав, 3 состава в очереди;
х5 – на горке один состав, 4 состава в очереди;
х6 – на горке один состав, 5 составов в очереди.
n-число подъездных путей(n=6) к горке и два подгорочных локомотива.
В приведенных выше расчетах для системы «парк приема – горка» не учитывался простой поездов по неприему станцией, в то время как он может иметь место.
С учетом этого расчет показателей системы для пуассоновского входящего потока поездов и показательного времени их обслуживания может производиться по формулам:
– средняя длина очереди на путях прибытия
,
где т – число путей в парке приема;
– среднее число поездов, задержанных по неприему станцией из-за недостатка приемных путей и недостаточной мощности горки
;
– вероятность задержки поездов по неприему станцией
;
– средний простой поездов на путях прибытия в ожидании расформирования
;
– средний простой поездов по неприему станцией
;
– сумма среднего времени ожидания на путях приема и среднего времени задержки по неприему станцией
.
Для пуассоновского входящего потока и произвольного распределения времени обслуживания (расформирования)
– среднее число составов, ожидающих расформирования в парке прибытия
;
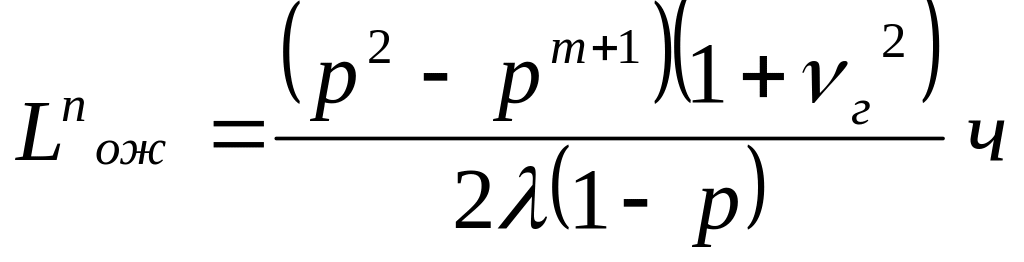– средний простой по неприему станцией
;
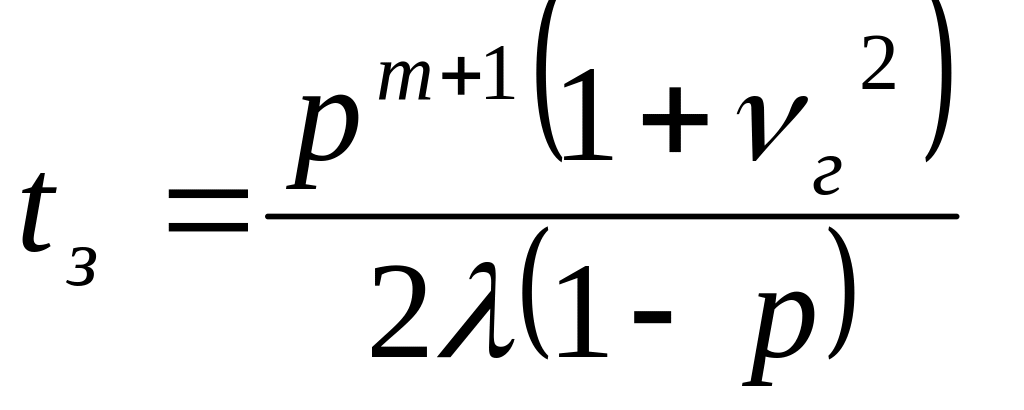– вероятность задержки поездов по неприему станцией
.
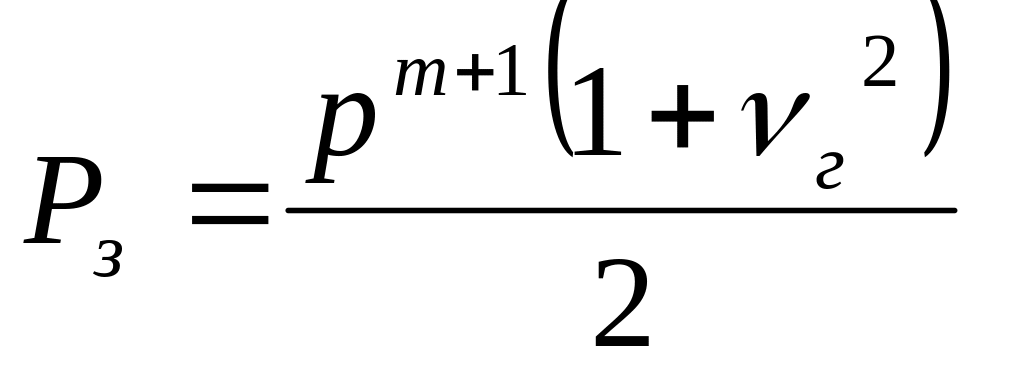Для эрланговского входящего потока и эрланговского времени распределения расчет показателей системы производится по формулам, приведенным в предыдущем разделе
ВЫВОДЫ:
Лабораторная работа № 9
Система № 3 - «сортировочный парк - вытяжки формирования» (система № 3 таблица 1).
|
n |
|
(n-1) |
|
(n-2) |
|
(n-3) |
|
(n-4) |
|
|
|
х0 |
|
х1 |
|
х2 |
|
х3 |
|
х4 |
|
х5 |
|
х6 |
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
|
х0 – система свободна, составов к формированию нет;
х1 – локомотив формирует 1 состав, очереди нет;
х2 – локомотив формирует 1 состав и 1 состав в очереди;
х3 – локомотив формирует 1 состав и 2 состава в очереди;
х4 – локомотив формирует 1 состав и 3 состава в очереди;
х5 – локомотив формирует 1 состав и 4 состава в очереди;
х6 – локомотив формирует 1 состав и 5 составов в очереди.
n-число составов(n=6) и два горочных локомотива
ВЫВОДЫ: