Лабораторная работа № 7

Расчет показателей системы «прилегающие участки – парк приема»

Расчет показателей системы рассмотрим на примере системы «прилегающий участок– парк приема» (система № 1 таблица 1).

Дано С прилегающего участка в парк приема станции в сутки поступает 72 поезда (N). В парке 7 путей. Осмотр и ремонт составов выполняют две бригады вагонников, продолжительность осмотра состава одной бригадой t_обр =0,5 ч.

Требуется Определить состояние системы массового обслуживания, среднее число составов, ожидающих обработки, среднюю длину очереди для пуассоновского входящего потока поездов и показательного времени обслуживания (осмотра, ремонта).

Решение

1) определим интенсивность входящего потока, среднюю длину очереди для пуассоновского входящего потока требований (поездов) в единицу времени (ч):

2) найдем интенсивность обслуживания требований (поездов):

3) определим устойчивость работы системы:

– система работает устойчиво,

где n – число бригад(n = 2).

4) составим граф состояния системы:

х0		х1		х2		х3		х4		х5		х6		х7
			2		2		2		2		2		2

Здесь х₀ – система свободна, поездов в парке приема нет;

х₁ – в парке приема 1 поезд, занята одна бригада; очереди нет;

х₂ – в парке приема 2 поезда, заняты 2 бригады; очереди нет;

х₃ – заняты 2 бригады, в очереди 1 поезд;

х₄ – заняты 2 бригады, в очереди 2 поезда;

х₅ – заняты 2 бригады, в очереди 3 поезда;

х₆ – заняты 2 бригады, в очереди 4 поезда;

х₇ – заняты 2 бригады, в очереди 5 поездов.

Дифференциальные уравнения, описывающие это состояние:

,

,

,

,

,

,

,

.

При левые части уравнений превратятся в нули, т.е. система дифференциальных уравнений превратится в систему алгебраических уравнений. Разделив каждое уравнение на и обозначим , получим:

;

;

;

;

;

;

;

.

;

;

;

;

;

;

.

5) определим состояние системы p₀, p₁, p₂,..., p₇,

;

;

;

;

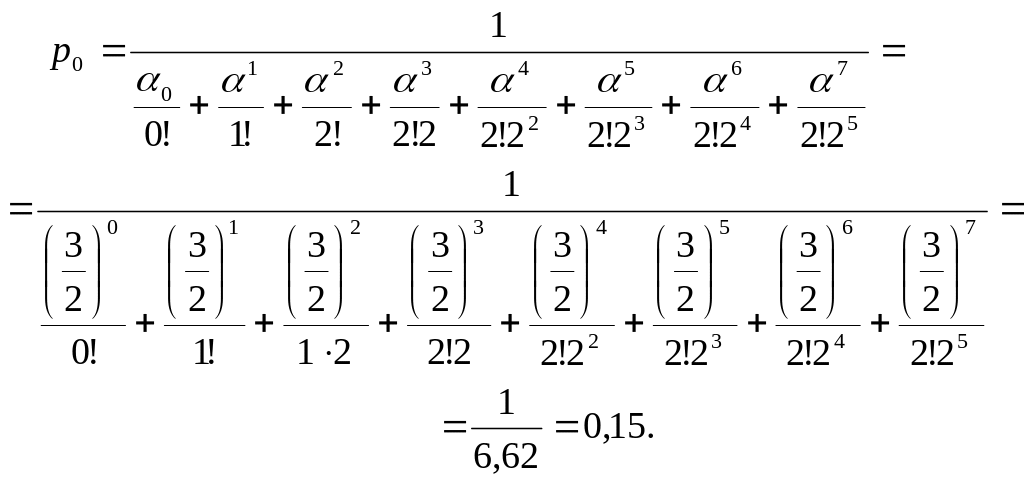
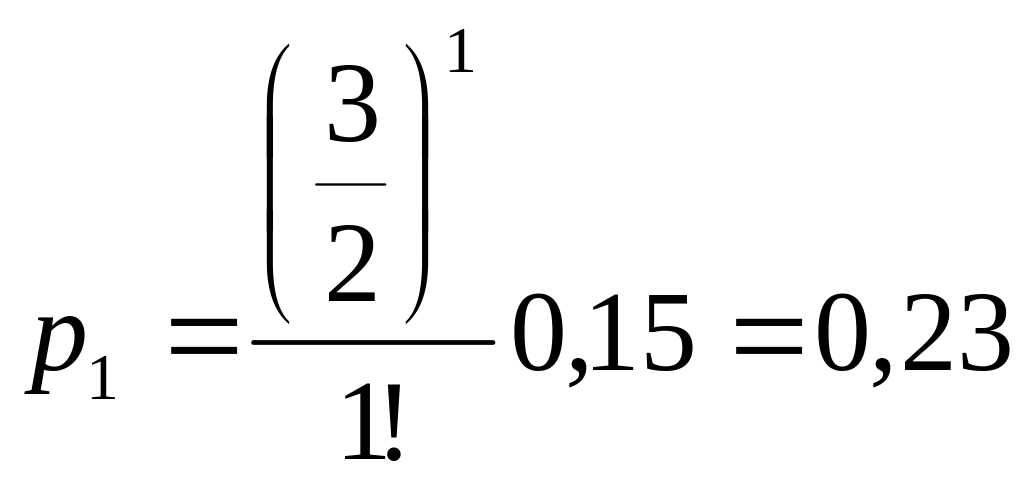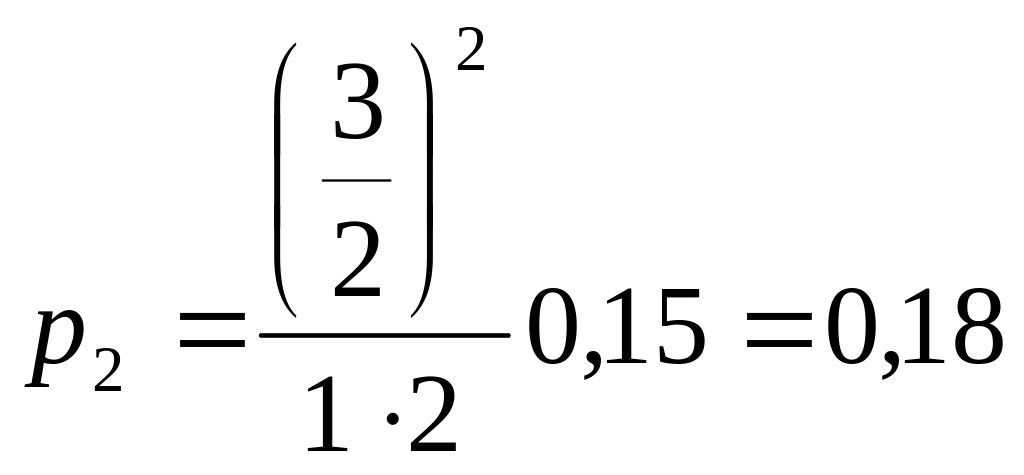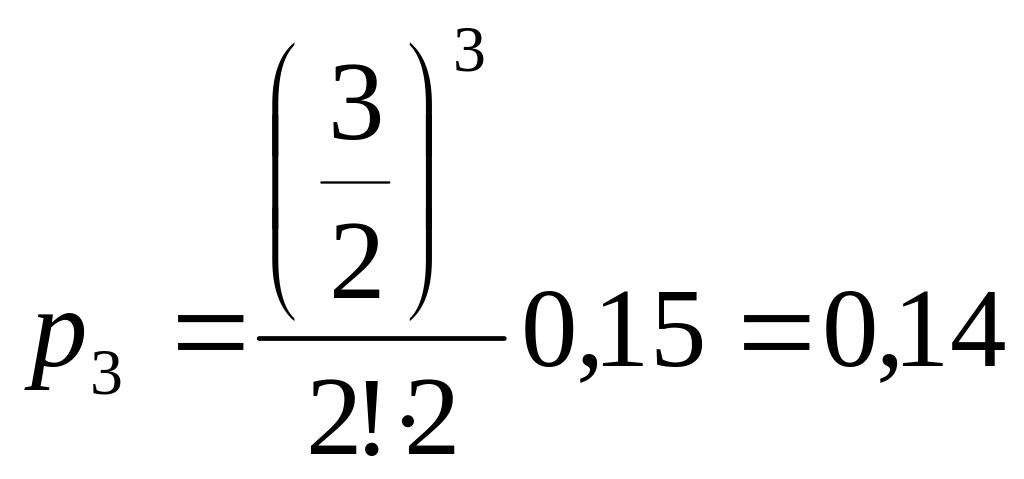аналогично p₄ = 0,10; p₅ = 0,09; p₆ = 0,06; p₇ = 0,05.

Сумма всех состояний системы:

0,15 + 0,23 + 0,18 + 0,14 + 0,10 + 0,09 + 0,06 + 0,05 = 1.

6) найдем среднее число составов в очереди:

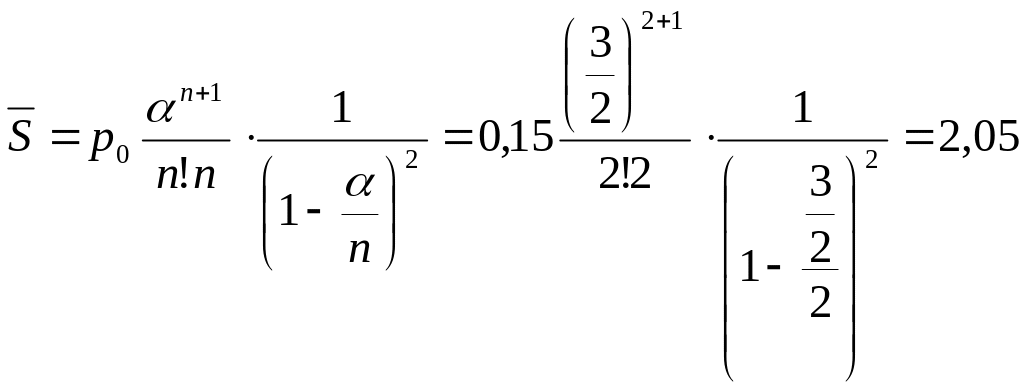состава.

7) определим среднее время ожидания обработки состава:

.

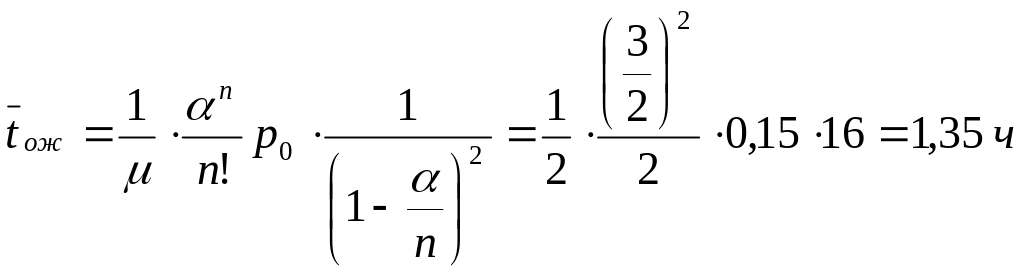Средняя потеря времени всеми заявками в сутки:

.

ВЫВОДЫ:

Поскольку средняя потеря времени всеми заявками в сутки в системе — «прилегающий участок – парк приема» велика, то следует изменить технологию работы ПТО вагонов и приёмосдатчиков.

Для других систем составим лишь графы их состояния, а все последующие расчеты предлагаем студенту выполнить самостоятельно, пользуясь указаниями, приведенными выше.