75

РОСЖЕЛДОР

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВПО РГУПС)

А.И. Филоненков

МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ НА ТРАНСПОРТЕ

Марковские случайные процессы

Учебно-методическое пособие

Ростов-на-Дону

2011

УДК 681.5(07)+06

Филоненков, А.И.

Математическое обеспечение автоматизированных систем управления и информационных технологий на транспорте. Марковские случайные процессы: учебно-методическое пособие / А.И. Филоненков; Рост. гос. ун-т путей сообщения, – Ростов н/Д, 2011. – 86 с. : ил.— Библиогр.: 3 назв.

Приведены необходимые сведения о применении теории систем массового обслуживания на железнодорожном транспорте и указания к выполнению работы по составлению математических моделей в управлении перевозочным процессом. Предназначены студентам факультетов УПП, АТС, ЗФ РГУПС.

Рецензент канд. техн. наук, проф. В.Н. Зубков (РГУПС),

© Ростовский государственный университет путей сообщения, 2011

Введение

Многообразие факторов, влияющих на выбор наиболее рациональных способов организации перевозочного процесса и технического оснащения железных дорог, требует решения сложных в математическом отношении задач. В последнее время получил развитие и широкое распространение ряд прикладных разделов математики. Для расчетов, связанных с эксплуатацией железных дорог, наибольший интерес представляют методы, позволяющие получить оптимальное решение задач.

Так, например, при нахождении оптимального плана формирования поездов, при выборе наиболее рациональных способов усиления пропускной и провозной способности линии, при разработке планов распределения порожних вагонов и решений других комбинаторных задач эксплуатации железных дорог широко используется математическое программирование (линейное, динамическое), теория множеств, теория графов и некоторые другие методы.

При решении многих вопросов, связанных с неопределенностью исходных данных (в частности, в связи с неравномерностью работы железных дорог) широкое распространение получает теория вероятностей, теория массового обслуживания, теория игр, методы статистических испытаний и др.

Изучение этих математических методов и их применения для решения практических задач является важнейшей задачей подготовки инженеров по эксплуатации железных дорог. Заданием на лабораторную работу предусмотрено решение задач, требующих знаний в области теории вероятностей и теории массового обслуживания, а также в области линейной алгебры и линейного программирования.

Лабораторная работа №1 марковские случайные процессы

Пусть имеется физическая система, которая под влиянием случайных факторов может переходить мгновенно из одного состояния в другое. Число состояний системы может быть конечно (или счетно). Тогда говорят, что в системе происходит случайный процесс с дискретным (или счетным) множеством состояний.

Рассмотрим входящий поток заявок в систему, как последовательность точек t1, t2, ... , ti, ... – моментов поступления заявок на оси времени Ot (рис.1.0) Здесь t0 – начальный момент.

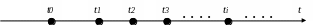
Рис. 1.0

Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то, вообще говоря, случайные моменты времени.

Случайный процесс, протекающий в какой-либо физической система S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для любого момента времени t₀ (рис. 1.1) вероятности любого состояния системы в будущем (при t > t₀) зависят только от ее состояния в настоящем (при t = t₀) и не зависят от того, когда и каким образом система S пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса - от прошлого).

t < t₀ (прошлое) t > t₀ (будущее)

t

t = t₀ (настоящее)

Рис. 1.1.

При этом, если переход из состояния в состояние происходит в строго фиксированные моменты времени , называемые шагами, то имеем Марковский случайный процесс с дискретным множеством состояний и дискретным временем (цепь Маркова с дискретным временем). Если переход из состояния в состояние происходит в случайные моменты времени, то имеем Марковский случайный процесс с дискретным множеством состояний и непрерывным временем (цепь Маркова с непрерывным временем).

1 Простейший поток событий – поток однородных событий, удовлетворяющий следующим условиям: стационарности, ординарности и без последействия, (без предыстории).

Поток событий называется стационарным, если вероятность того, что за промежуток времени произойдет m событий потока, зависит только от длины интервала времени и не зависит от начала его отсчета . Интенсивность потока (среднее число событий в единицу времени) для стационарного потока постоянна. Это позволяет рассчитывать характеристики системы в среднем.

Поток событий называется потоком без последействия, если для любых непересекающихся промежутков времени число событий, приходящихся на один из них, не зависит от того, сколько событий произошло за другие промежутки времени.

Поток событий называется ординарным, если вероятность того, что за малый промежуток времени произошло не менее двух событий, пренебрежимо мала по сравнению с вероятностью того, что за промежуток времени произошло одно событие. Это означает, что события в систему поступают по одному.

Стационарный, ординарный без последействия поток называется простейшим потоком (или потоком Пуассона). Нестационарный, ординарный без последействия поток называется нестационарным потоком Пуассона.

Промежуток времени Т между двумя соседними событиями простейшего потока распределен по показательному (экспоненциальному) закону с параметром . Его среднее значение (математическое ожидание) и среднее квадратическое отклонение равны , т.е. математическое ожидание и среднее квадратическое отклонение равны.

При рассмотрении процессов, протекающих в системах с дискретным множеством состояний и непрерывным временем, можно считать, что переход системы из состояния в состояние происходит под действием потоков событий. Если все потоки, переводящие систему из состояния в состояние, будут пуассоновские (стационарные или нестационарные), то процесс, протекающий в системе, будет марковским.