Задание 2.2. Сложное движение точки. Определение абсолютной скорости и абсолютного ускорения точки

Точка M движется относительно тела D. По заданным уравнениям относительного движения точки M и движения тела D определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки M.

Схемы механизмов показаны на рис. 1–29, а необходимые для расчета данные помещены в табл. 2.3.

Таблица 2.3

Номер вари- анта (рис. 1–28)	Уравнение отно-сительного дви-жения точки MOM=sr=sr(t), см	Уравнение движения тела						Доп. данные
1	2	3	4	5	6	7	8	9
1			-		-	25	-
2			-		20	-	-
3			-	2	-	30	-
4			-	1	-	-	60
5			-	2	30	-	-
6	-	-			15	-	-
7			-		-	40	60
8			-	2	-	-	30
9			-		-	-	-
10			-		20	20	-
11			-	4	-	25	-
12			-	2	30	30	-
13			-		40	-	-
1	2	3	4	5	6	7	8	9
14			-		-	-	30
15			-	2	-	60	45
16			-		-	20	-
17			-	1	-		-
18			-	2	-	-	60
19			-	2	40	-	-
20			-	3	60	-	-
21			-		25	-	-
22			-		30	-	-
23		-	-	1	18	-	-
24			-	1	30	-	-
25			-	5	-	-	-
26			-		-	-	45
27	-	-		2	75	-	-
28			-	2	40	-	-
29		-		2	48	-	-

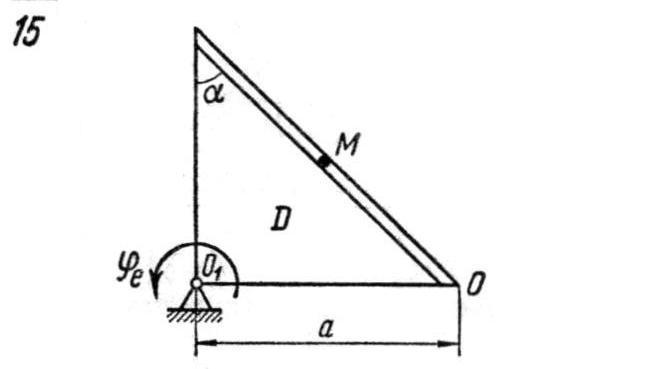
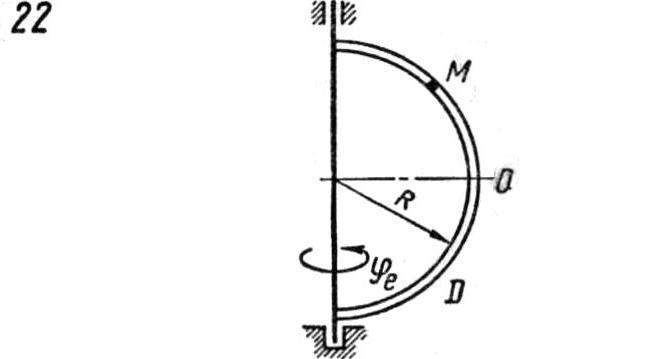
Примечания. Для каждого варианта положение точки M на схеме соответствует положительному значению s_r; в вариантах 5, 10, 12, 13, 2024, 2829 OM = s_r – дуга окружности; на схемах 5, 10, 12, 21, 24 OM – дуга, соответствующая меньшему центральному углу. Относительное движение точки M в вариантах 6 и 27 и движение тела D в варианте 23 определяются уравнениями, приведенными в последнем столбце табл. 2.3.

Пример выполнения задания

Дано: схема механизма (рис. 2.7), , , , , .

Найти: абсолютные скорость и ускорение точки М.

Решение. Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью Д. Положение точки M на теле Д определяется расстоянием .

При ,

Угол вычисляется из длины дугиОМ

,

откуда находим значение угла

.

Абсолютную скорость точки M найдем как геометрическую сумму относительной и переносной скоростей:

.

Модуль относительной скорости

,

где

.

При t = 2 с

, .

Положительный знак у показывает, что векторнаправлен в сторону возрастания.

Модуль переносной скорости

, (2.1)

где точка M, как и AO участвует в поступательном движении тела Д (т.е. AO всегда параллельна самой себе).

.

При t = 2 c

.

Направлениесовпадает с направлением отсчета угла, следовательно, векторнаправлен перпендикулярно плоскости чертежа от нас.

Тогда, согласно формуле (2.1) модуль переносной скорости:

.

Вектор направлен по касательной к окружностиO₂A в сторону вращения тела Д. В момент времени t = 2 c положение тела Д таково, что значение угла составляетрад. Следовательно, векторнаправлен вертикально вниз (рис. 2.8). Так как векторне перпендикулярен вектору, то для нахождения модуля абсолютной скорости используем теорему косинусов:

Абсолютное ускорение точки M равно геометрической сумме относительного, переносного и кориолисова ускорений:

или в развернутом виде

Модуль относительного касательного ускорения

,

.

Приt = 2 c

.

Знаки иодинаковы, следовательно, относительное движение точкиМ ускоренное.

Относительное нормальное ускорение

.

Угловое переносное ускорение находим как

.

Приt = 2 c

Модуль переносного центростремительного ускорения

,

а модуль переносного вращательного ускорения

.

При t = 2 c

, .

Модуль кориолисова ускорения

.

Так как вектор направлен перпендикулярно плоскости чертежа от нас, то угол между направлениями векторови равен, и тогда

.

Покажем направление ускорений точки M в момент времени (рис. 2.9). Векторнаправлен по правилу векторного произведения вдоль направленияMА.

Модуль абсолютного ускорения точки М находим способом проекций:

,

,

.

После вычисления получаем: