Дәріс №15-16. Электрқозғалтқышын таңдау және олардың жылулық жұмыс режимдері.

1.Жұмыс режимдері. Электрқозғалтқышының жылулық күйі.

2.Электрмашиналары температурасының өзгеру заңдылықтары.

3.Ұзақ уақытты жүктеме үшін қозғалтқыштың қуатын таңдау.

Электр машинасы – мех. энергияны электр энергиясына және керісінше немесе параметрлері белгілі электр энергиясын басқа параметрлі электр энергиясына түрлендіретін машина. Ол токтың тегіне қарай тұрақты ток машинасы (мыс., тұрақты ток генераторы, тұрақты ток қозғалтқышы) және айнымалы ток машинасы (асинхронды генератор, асинхронды қозғалтқыш, синхронды генератор, синхронды электр қозғалтқышы, коллекторлы генератор, коллекторлы қозғалтқыш) болып, ал пайдалану мақсатына қарай генератор, қозғалтқыш, электр машиналық түрлендіргіш (мыс., қозғалтқыш генератор, бір зәкірлі түрлендіргіш, фаза түрлендіргіш, т.б.) электр машиналық күшейткіш болып ажыратылады. Э. м-на электрстатик. машина да жатқызылады.

Сандық жүйенің бір каналының құрылымдық сұлбасын келесі түрде келтіруге болады (сурет 1):

y

1 сурет.

Сандық есептеуіш машинасы басқарудың сызықты алгоритмін жүзеге асырады делік, ал кешігудің қосынды уақыты 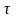жүйенің үздіксіз бөлігіне сәйкестендірілген.

АЦП-да жүзеге асырылатын аналогтік g(t) немесе y(t) шаманың сандық 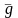немесе кодқа түрлену процесі үш операциядан құрылады: уақыт бойынша кванттау, деңгей бойынша кванттау және кодтау.

Уақыт бойынша кванттау АЦП-дағы ақпараттың командалар бойынша СЕМ-дан уақыттың t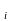 =iT моменттерінде енгізілетіндіктен пайда болады. Деңгей бойынша кванттау процесінде үздіксіз шаманың өзерудің бүкіл диапазоны өзара тең бөліктерге бөлінеді. Кедлесі шама

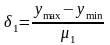
АЦП-ның ажырату қабелетін анықтайды.

Кодтау процесінде интервалыныің әрқайсысына анықталған екілік код сәйкестендіріледі.. Бұндай сәйкестендірілу бірмәнді болу үшін, келесі шарт орныдалу керек

,

мұндағы 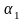- екілік разрядтардың саны.

Линеаризацияланған сипаттама үшін АЦӨ-дағы беріліс коэффициенті

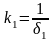
ЦАӨ сандық есептеуіш машинадан келетін кодты в аналогтік u* дабылға түрлендіреді,

Түрлендіру процесінде кодтың әрбір мәніне үздіксіз u дабылдың анықталған тіркелген мәні сәйкес келеді, ал бұл деңгей бойынша квантталудың болатындығын білдіреді. Нольден өзгеше рұқсат етілген деңгейледің саны

,

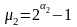мұндағы 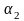- ЦАП разрядтар саны.

Уақыттың =iT моментінде u(iT) үздіксіз дабылдың алынған мәндері тіркеледі де, Т дискреттіліктің периоды кезінде бір деңгейде ұсталынады. Ал бұл ЦАП-дағы беріліс W_Ф(s) функциясына ие болатын құрылушы құрылғының бар болуына сәйкес келеді.

СЕМ басқарудың қажетті алгоритмін құрады немесе келесі сызықтық айырғыш теңдеумен берілетін есептеуіш процедура түріндегі дискреттік коррекцияны іске асырады:

.

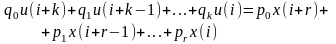
Нольдік бастапқы шарты кезінде теңдеуге z-түрлендіруді қолдансақ, келесі СЕМ –нің беріліс функциясын аламыз:

Бастапқы құрылымдық сұлбаны келесі түрде түрлендіруге болады (сурет 2):

2 Сурет.

АЦП мен ЦАП-тың беріліс коэффициенттері, сонымен бірге кешігу жүйенің үздіксіз бөлігіне сәйкестендіріледі.

Сандық жүйенің құрылымдық сұлбасы импульстік жүйенің құрылымдық сұлбасынан D(z) беріліс функциясына ие болатын қатардың болуымен ерекшелінеді.

Тұйықталмаған сандық жүйенің беріліс функциясы

W(z)=D(z)W_O (z).

Сандық жүйелерге импульстік жүйелерді талдау кезіндегі қолданылатын орнықтылықты зерттеудің барлық әдістері таралады.

Жүйе орнықты болады, егер оның сипаттамалық теңдеуінің барлық түбірлері бірлік радиусы болатын шеңбердің ішнде жататын болса.Егер де түбірлердің біреуі шеңберден тыс жатса, онда жүйе орнықсыз деп есептелінеді.

Жүйе орнықтылықтың апериодты шекарасында болады, егер де оның сипаттамалық теңдеуінде z=1 түбір бар болса, ал қалған түбірлері бірлдік радиусты шеңбердің ішінде жатса.

Егер де сипаттмалық теңдеуде бірлік радиусты шеңберде орналасқан комплексті-түйіндескен түбірлердің жұбы болса, онда мұнда орнықтылықтың тербелмелі шекерасы орын алады. Бұл жағдайда уақыттың өтуімен жүйеде өшпейтін периодты тербелістер пайда болады.

Импульстік жүйелер үшін типтес үшінші типті орнықтылықтың шекарасы болып табылады, оған сипаттамалық теңдеудегі z = -1 түбірдің бар болуы сәйкес келеді. Бұл жағдайда жүйеде периоды 2T болатын өшпейтін тербелістер пайда болады.