1.2.1. Многочлени -го степеня.
А. Многочлениз комплексними коефіцієнтами від комплексноїзмінної.
Означення.
Многочленом
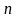-го
степеня називається
функція
де
– сталі комплексні
числа (коефіцієнти многочлена),
,
–
комплексна змінна. Число
,
у якому многочлен приймає нульове
значення (
),
називається коренем
многочлена.
Справедлива
теорема,
яка називається основною
теоремою алгебри: будь
який многочлен степеня
має комплексний корінь.
Нехай
– довільна точка комплексної площини.
Представимо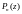
у вигляді многочлена
по степеням
:
.
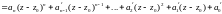Тут
–
нові значення коефіцієнтів, що отримуються
після розкриття степенів і зведення
подібних членів. Очевидно,
,
звідси слідує твердження: для того, щоб
число
було коренем многочлена
,
необхідно і достатньо, щоб коефіцієнт
при нульовому степені у розкладі
по степеням
був рівний нулю:
.
Але тоді
.
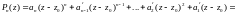
Таким чином, доведена
Теорема
Безу: для того, щоб
многочлен
-го
степеня
мав
комплексний корінь
,
необхідно і достатньо, щоб він без остачі
ділився на
,
тобто щоб
представлявся у вигляді: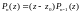
,
де
– многочлен (
–1)-го
степеня.
Нехай – корінь многочлена , тоді, по теоремі Безу, . Можливі два варіанти:
1. Число не є коренем многочлена , в цьому випадку називається простим коренем многочлена .
2. Число
є коренем многочлена
,
тоді, використовуючи теорему Безу уже
до
,
отримаємо
,
.
Використовуючи до
ті ж роздуми, прийдемо до висновку: якщо
– корінь многочлена
,
то
єдиним
чином представляється у вигляді
,
де
.
Число
в цьому випадку називається кратністю
кореня
.
Згідно
основної теореми алгебри, будь який
многочлен
при
має
хоча б один корінь
;
якщо кратність цього кореня рівна
,
то, згідно викладеного,
представляється у вигляді
,
де
.
Якщо
,
то многочлен
має
корінь
,
і представляється у вигляді
.
Якщо
,
ці викладки можна продовжити; кінцевий
висновок формулюється так: будь який
многочлен
степеня
при старшому коефіцієнті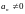
єдиним
(з точністю до порядків співмножників)
чином може бути представлений у вигляді
,
де
–
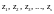(попарно різні) корені многочлена,
їх кратності,
– кількість різних
коренів. Загальна кількість коренів
многочлена з урахуванням їх кратностей
рівна
:
.
Б.
Многочлени з дійсними коефіцієнтами.
Розглянемо многочлен
від
комплексної змінної
,
якщо його коефіцієнти
– дійсні числа. Сформулюємо ряд
властивостей такого многочлена.
1.
Якщо
–
число, спряжене до числа
,
то
.
2.
Якщо
– корінь многочлена
,
то
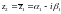– також корінь цього
многочлена.
3.
Якщо
– корінь многочлена з дійсними
коефіцієнтами
,
то
без остачі ділиться на квадратний
тричлен
,
де
.
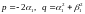4. Якщо – корінь многочлена кратності , то – корінь цього ж многочлена тієї ж кратності.
5. Будь який многочлен -го степеня може бути представлений, і притомуєдиним (з точністю до порядку співмножників)чином, увигляді
,
де
–
попарно різні дійсні корені цього
многочлена,
– їх кратності,
квадратні тричлени (відповідають попарно
різним парам спряжених коренів
кратностей
)
з дійсними коефіцієнтами
не мають дійсних коренів (тобто
),
.