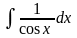Интегральное исчисление

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Первообразная функция

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:

F(x) = f(x).

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F₁(x) = F₂(x) + C.

Неопределенный интеграл

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

2.

3.

4. где u, v, w – некоторые функции от х.

5. 

Таблица интегралов

Таблица 1 – Интегралы некоторых элементарных функций

Интеграл		Значение		Интеграл			Значение
1			-lncosx+C		9		ex + C
2			lnsinx+ C		10		sinx + C
3					11		-cosx + C
4					12		tgx + C
5					13		-ctgx + C
6			ln		14		arcsin + C
7					15
8					16

7.4. Методы интегрирования

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования можно сделать вывод, что искомый интеграл равен , где С – некоторое постоянное число. Однако, с другой стороны . Таким образом, окончательно можно сделать вывод:

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Пример. Найти неопределенный интеграл .

Сделаем замену t = sinx, dt = cosxdt.

Интегрирование по частям.

Способ основан на применении формулы интегрирования по частям ;

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Вопросы для самоконтроля

1. Что такое первообразная функция?

2. Какими свойствами обладает неопределённый интеграл?

3. Чему равен неопределенный интеграл функции lnx?

4. В чем суть метода подстановки (замены переменной) в неопределенном интеграле?

5. В чем состоит метод неопределенных коэффициентов при интегрировании рациональныхдробей?

Определенный интеграл Понятие определенного интеграла

Пусть на отрезке [a, b] задана непрерывная функция f(x).

y

M

m

0 a x_i b x

Рисунок 1. Составление интегральной суммы.

Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

x₀ < x₁ < x₂ < … < x_n

Тогда x₁ – x₀ = x₁, x₂ – x₁ = x₂, … ,x_n – x_n-1 = x_n;

Внутри каждого отрезка выберем некоторую точку .

x₀ < ₁ < x₁, x₁ <  < x₂, … , x_n-1 <  < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].

S_n = f(₁)x₁ + f(₂)x₂ + … + f(_n)x_n =

Определение: Если при любых разбиениях отрезка [a, b] и произвольном выборе точек _i интегральная сумма стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].

Обозначение :

а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.

Определение: Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.