3.6 Принцип относительности Галилея

До сих пор мы рассматривали движение относительно тел отсчета, жестко связанных с Землей, которую считали неподвижной. Естественно поставить вопрос: будут ли законы динамики, полученные для систем отсчета, связанных с неподвижными телами, справедливы для систем отсчета, связанных с движущимися телами?

Рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью (рисунок 14). Одну из этих систем (К) будем условно считать неподвижной. Другая же система (К') пусть движется равномерно и прямолинейно со скоростью относительно первой. Движение тела в подвижной системе отсчета называется относительным движением, а в условно неподвижной - абсолютным движением. Движение тела относительно неподвижной системы отсчета, которым оно обладало бы, будучи жестко связанным с одной из точек подвижной системы, называется переносным движением.

В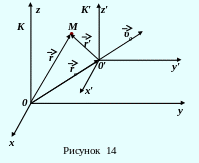 начальный момент времени, т.е. при t = 0, 0 и 0′ совпадали. Положение системы К′ в некоторый момент времени t определится радиус – вектором

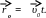
П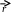 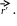оложение некоторой точки М относительно системы К определится радиус-вектором , относительно системы К′ - Из рисунка (14) следует:

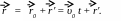
(3.54)

В проекциях на координатные оси соотношение (3.54) имеет вид:

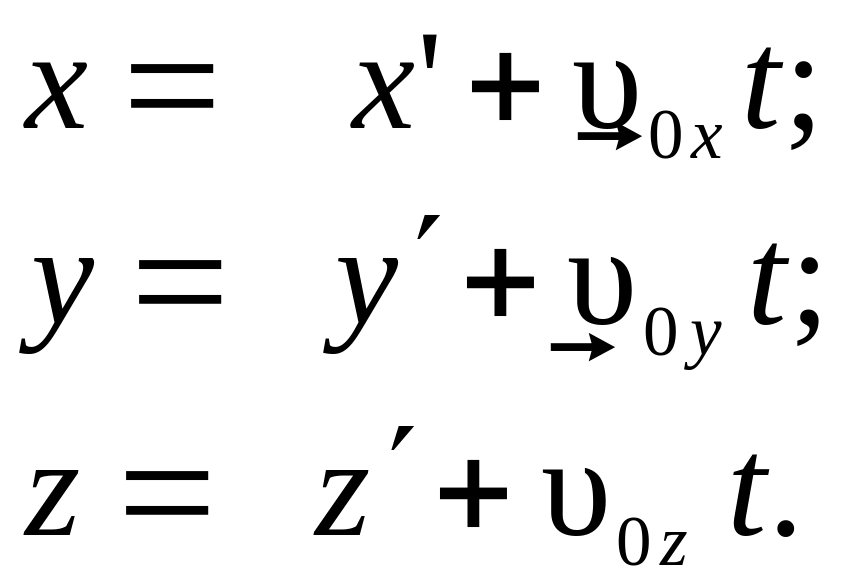_(3.55)

Соотношения (3.55) называются преобразованиями Галилея. В классической механике считается, что t = t′. Дифференцируя формулы (3.55)

по времени, получим классический закон сложения скоростей:

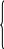
(3.56)

.

Здесь , , - это проекции вектора относительной скорости тела (по отношению к системе отсчета К'), а , , - это проекции вектора абсолютной скорости  (по отношению к системе отсчета К). В векторной форме закон сложения скоро­стей имеет вид

. (3.57)

Продифференцировав выражение (3.56) и (3.57) по времени, получим, что компоненты ускорений в подвижной и неподвижной системах отсчета будут одинаковыми, а также вектора абсолютного и относительного ускорений тела равны:

.

Это может быть лишь в случае, если . Отсюда вытекает механический принцип относитель­ности Галилея. Согласно этому принципу все законы механики должны иметь одинаковый вид во всех инерциальных системах отсчета. Другими словами, уравнения, описывающие законы механики, должны быть инвариантными по отношению к преобразованиям Галилея. Принцип относительности Галилея часто формулируется так:

находясь в инерциальной системе, никакими механическими опытами нельзя установить, движется эта система равномерно и прямолинейно или она находится в покое.

Таким образом, все инерциальные системы отсчёта равноправны между собой.