3 Механика

3.1 Физическое содержание механики

Механика изучает простейшую форму движения материи, которое состоит в перемещении тел или частей тела относительно друг друга. Как и другие естественные науки, механика устанавливает свои положения на основе обобщения опытных данных. Опыты над перемещением тел являются простейшими, поэтому механика развилась раньше других естественных наук. Основные законы механики были в значительной мере выяснены Галилеем (1564 – 1642) и окончательно сформулированы Ньютоном. Л. Эйлер, много лет работавший в Петербургской Академии наук, впервые придал законам механики аналитический вид и сыграл большую роль в её развитии. Однако механика Галилея–Ньютона, получившая название «классической», возникла в результате наблюдений над ограниченным типом движений, а именно, движений тел сравнимых с размерами человеческого тела (брошенный камень)

и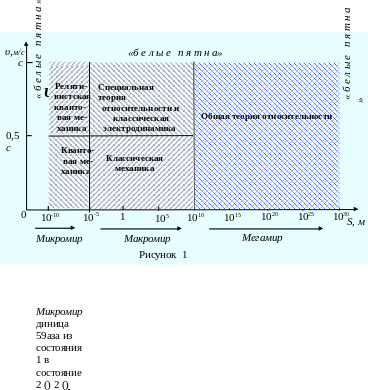 ли очень больших по сравнению с ним (движение планет) и движущихся с небольшими скоростями. Отсюда – приближенный характер классической механики. Дальнейшее развитие науки показало, что законы классической механики справедливы лишь для макротел, движущихся со скоростями υ много меньшими скорости света с ( υ << с). Движение макротел со скоростями, сравнимыми со скоростью света (υ ~ с), описывается релятивистской механикой (теорией относительности). Законы движения микроскопических тел (атомов, элементарных частиц) устанавливаются квантовой механикой. На рисунке 1 представлена схема, иллюстрирующая границы применения важнейших (фундаментальных) физических теорий с элементами и понятиями которых в той или иной степени предстоит познакомиться при изучении базового курса физики. В данном случае границы применимости (разумеется, приблизительные и расплывчатые) ограничены определёнными пространственно-временными областями и скоростями движения. «Белые пятна» на схеме отражают пока неизведанные области вечно движущегося материального мира.

Изучение физики начинаем с классической механики, которая состоит из трёх разделов: кинематики, статики и динамики.

Кинематика - изучает движение тел, не рассматривая причины, которые вызывают или изменяют это движение.

Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия, поэтому законы статики отдельно от законов динамики в вузовском курсе физики не рассматриваются.

Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение.

3.2 Кинематика материальной точки

3.2.1 Основные понятия

При исследовании явлений окружающего мира физика широко использует метод моделирования, при котором принимаются во внимание только существенные для данного круга явлений свойства и связи.

Для построения моделей механических систем важнейшей абстракцией является понятие материальной точки. Материальной точкой называют физический объект, размерами и формой которого в условиях данной задачи можно пренебречь. Таким образом, в геометрическом смысле этот объект эквивалентен математической точке, но обладает массой. Например, полёт пули или движение камня можно рассматривать как движение материальной точки. Однако если необходимо учитывать сопротивление среды, оказываемое на пулю или камень, то эти тела уже нельзя рассматривать как материальные точки.

Абсолютно твёрдым телом называют тело, расстояние между любыми двумя точками которого в условиях данной задачи можно считать неизменным,

т.е. это тело, размеры и форма которого не изменяются при движении. Абсолютно твёрдое тело обычно рассматривают как систему жёстко связанных между собой материальных точек.

Положение тела в пространстве можно определить лишь по отношению к другим телам. Абсолютно твёрдое тело, по отношению к которому рассматривается движение исследуемых тел, называется телом отсчёта. В качестве тела отсчёта может быть выбрана неподвижная точка, например, начало системы координат.

Для характеристики положения различных точек пространства относительно тела отсчёта вводится система координат, которую жёстко связывают с телом отсчёта. Существуют различные системы координат – сферическая, цилиндрическая, прямоугольная, полярная и др. Мы, в основном, будем пользоваться прямоугольными декартовыми системами координат.

Тело отсчёта, связанная с ним система координат, вместе с прибором для отсчёта времени составляют систему отсчёта.

Линия, которую описывает материальная точка, перемещаясь в пространстве, называется траекторией. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. В различных системах отчёта траектория движения может быть разной. Например, шар, находящийся на вращающейся платформе, начинает движение от её центра. Относительно платформы траектория движения шара вдоль радиуса является прямолинейной. Это же движение относительно системы отсчёта, связанной с землёй, происходит по развёртывающейся спирали, т.е. является криволинейным.

Сумма длин отрезков траектории, описанной материальной точкой за какой-то промежуток времени, называется длиной пути (ΔS), пройденного материальной точкой за это время (рисунок 2).

Р адиус-вектором материальной точки называется вектор (рисунок 2), проведённый из точки отсчёта О, к положению рассматриваемой точки в данный момент времени.

В ектор, проведённый из начального положения движущейся материальной точки в её конечное положение, называется вектором перемещения ( ). Из рисунка 2 следует, что:

, (3.1)

где равенство имеет место при прямолинейном движении.

Опытным путём установлен закон независимости движений: если точка одновременно участвует в нескольких движениях, то результирующее перемещение материальной точки равно векторной сумме перемещений, совершаемых ею за то же время в каждом из отдельных движений.

2. Способы задания движения материальной точки

Описать движение материальной точки – значит указать её положение в любой момент времени. При своём движении она проходит непрерывную последовательность точек системы отсчёта, т.е. описывает траекторию. Положение точек системы отсчёта можно характеризовать различными способами, в соответствии с которыми можно описывать и движение точки.

Описание движения в векторной форме. Положение материальной точки задаётся с помощью радиус-вектора относительно некоторой неподвижной точки, принятой за начало отсчёта. Такое задание положения материальной точки не предполагает введения системы координат, а требует лишь задание начала отсчёта. При движении материальной точки радиус-вектор непрерывно меняется, конец его описывает траекторию движения. Движение задаётся в виде функции радиус-вектора от времени:

. (3.2)

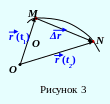
Из рисунка 3 следует, что вектор перемещения равен разности радиус-векторов в конечный и начальный моменты времени:

= . (3.3)

Описание движения в координатной форме.

В прямоугольных декартовых координатах положение материальной точки М задаётся координатами х, у, z (рисунок 4). При движении точки координаты меняются. Указывается зависимость координат х, у, z материальной точки от времени:

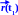х = х (t), y = y (t), z = z (t). (3.4)

И сключив из этих трёх уравнений время, можно получить уравнение траектории движения материальной точки.

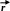К оординатную форму задания движения можно связать с векторным описанием движения. Для этого начало отсчёта надо связать с началом декартовой системы координат и провести радиус-вектор к п оложению материальной точки М в данный момент времени t (рисунок 5). Введя единичные векторы , радиус-вектор в любой момент времени можно выразить через его компоненты:

, (3.5)

т.к. - функция времени, то и x, y, z – функции времени. Согласно формуле (3.3), модуль вектора перемещения можно представить в виде:

. (3.6)

Описание движения с помощью параметров траектории. Если траектория задана, то задача сводится к указанию закона движения материальной точки вдоль этой траектории. Некоторая точка траектории принимается за начальную, а любая другая точка траектории характеризуется расстоянием S вдоль неё от начальной точки. В этом случае движение описывается формулой:

S = S (t). (3.7)

Например, прямолинейное равноускоренное движение описывается формулой:

.

3.2.3 Скорость

Скорость - является векторной величиной, которая определяет как быстроту движения, так и его направление в данный момент времени.

Средней путевой скоростью называется скалярная величина, равная отношению пути к тому промежутку времени, за которое этот путь пройден

. (3.8)

Т.к. , то .

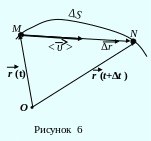
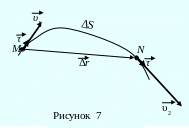
Средняя скорость перемещения - это векторная величина, численно равная отношению вектора перемещения к тому промежутку времени, за который это перемещение произошло:

. (3.9)

Направление вектора средней скорости перемещения совпадает с направлением (смотри рисунок 6).

При неограниченном уменьшении (при этом точка N стремится к точке M), средняя скорость перемещения стремится к предельному значению, которое

называется мгновенной скоростью или скоростью в данной точке:

. (3.10)

Вектор мгновенной скорости для каждого момента времени направлен по касательной к траектории в сторону движения, т.е.

, (3.11)

где - единичный вектор касательной.

По мере уменьшения путь все больше приближается к , поэтому модуль мгновенной скорости

. (3.12)

Вектор скорости можно разложить на составляющие по координатным осям:

. (3.13)

С другой стороны, подставляя в формулу (3.10) выражение (3.5), получим:

. (3.14)

Из сравнения выражений (3.13) и (3.14) следует, что

. (3.15)

При координатном способе задания движения модуль мгновенной скорости равен:

. (3.16)

Если при движении точки модуль ее скорости не изменяется, то движение называется равномерным.

Скорость результирующего движения материальной точки, участвующей одновременно в нескольких движениях, определяется как геометрическая сумма всех векторов скоростей отдельных движений, в которых участвует материальная точка: .

Е сли выражение проинтегрировать в пределах от до , то найдем длину пути, пройденного точкой за время :

. (3.17)

В случае равномерного движения и

.

В общем случае

.

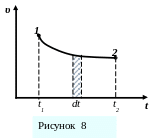
По графику скорости можно найти путь, пройденный телом. За бесконечно малый промежуток времени dt он численно равен площади заштрихованной фигуры (рисунок 8). Путь, пройденный за время Δt = t₂ - t_1, равен площади криволинейной трапеции заключенной между кривой зависимости и осями координат (рисунок 8): площадь t₁-1-2-t_2.

3.2.4 Ускорение

У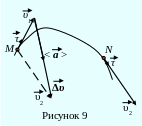 скорение – это физическая величина, характеризующая быстроту изменения вектора скорости.

Пусть при движении материальной точки из положения М в положение N, в течение промежутка времени от до , её скорость изменяется от значения до (рисунок 9 ). Вектор изменения скорости .

Средним ускорением за время , называется вектор, численно равный отношению изменения вектора скорости к промежутку времени, за которое это изменение произошло:

. (3.28)

Направление   совпадает с направлением (рисунок 9) .

Мгновенным ускорением называют векторную величину, численно равную пределу, к которому стремится среднее ускорение за промежуток времени , при .

. (3.19)

Используя соотношение (3.10), получим:

. (3.20)

Согласно уравнению (3.20) вектор мгновенного ускорения равен первой производной от вектора скорости по времени или второй производной от вектора перемещения по времени. Подставляя в формулу (3.20) выражение (3.5), получим формулу ускорения в координатной форме:

, (3.21)

где , , - компоненты вектора ускорения в декартовой системе координат. Модуль вектора ускорения в этом случае определяется по формуле:

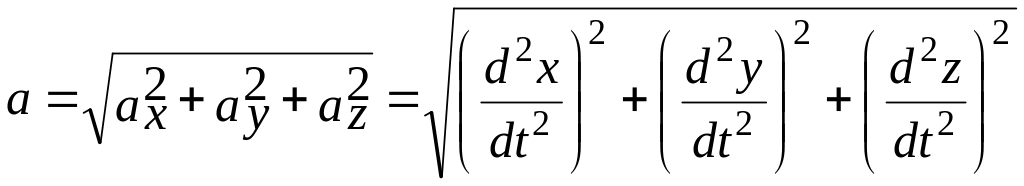. (3.22)

Вектор скорости характеризуется величиной и направлением. В общем случае произвольного криволинейного движения вектор скорости может изменяться и по величине (модулю) и по направлению. Оказывается, что вектор ускорения можно разложить на две составляющие, одна из которых характеризует быстроту изменения только модуля скорости, а другая – быстроту изменения направления скорости. Покажем это на примере простейшего движения по плоской траектории.

Допустим, за время Δt материальная точка переместилась из точки М в

точку N. При этом скорость её изменилась от до (рисунок 10). Мгновенное ускорение, например, в точке М:

.

Перенесём в точку М ( ) и отложим на МЕ модуль вектора :

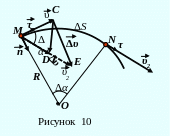
MD = =| |.

Проведём вектор . Тогда и

.

Рассмотрим каждое слагаемое.

1) . Направление вектора совпадает с направлением касательной к траектории в точке N. Вводя единичный вектор касательной , получим: . Численное значение равно изменению скорости по величине: | | =| | = . Таким образом:

. (3.23)

называется касательной или тангенциальной составляющей ускорения. Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости только по величине; она направлена по касательной к траектории движения материальной точки.

Обратите внимание: полное ускорение и тангенциальное ускорение две разные физические величины.

2) Рассмотрим второе слагаемое

вектор характеризует изменение направления скорости за время Δt. Для определения величины и направления этой составляющей ускорения

восстановим в точках М и N перпендикуляры к касательным до их пересечения в точке О (рисунок 10). Если Δt мало, то точки М и N близки, и дуга МN представляет собой отрезок окружности с радиусом кривизны R. R ≈ ОМ ≈ ОN и ΔS = RΔα. Угол СМD равен Δα, как углы с взаимно перпендикулярными сторонами. Из подобия треугольников МОN и СМD следует:

, ,

В последнем выражении значок «1» опускаем, ввиду произвольности выбора точки М. При Δt → 0 будет неограниченно приближаться к υ₁ по величине и направлению. При этом Δα → 0 и в пределе займёт положение нормали к касательной в точке М. Введём единичный вектор нормали , тогда

(3.24)

- нормальная составляющая ускорения, характеризует быстроту изменения скорости по направлению; она направлена вдоль нормали к касательной к траектории движения материальной точки к центру кривизны.

Соотношение для нормального ускорения (3.24) справедливо не только для плоского движения, но и для любого движения, только вместо радиуса окружности r надо подставлять радиус кривизны траектории.

П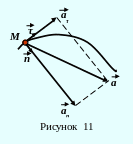 ри равномерном движении по окружности тангенциальное ускорение отсутствует. Полное ускорение равно нормальному ускорению и направлено по радиусу окружности к ее центру. Поэтому нормальное ускорение часто называют центростремительным.

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих ускорения (рисунок 11):

. (3.25)

Модуль ускорения можно определить по формуле:

. (3.26)