4.3 Основное уравнение молекулярно-кинетической теории газов

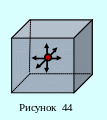
Основной задачей молекулярно-кинетической теории является установление связи между макро- и микропараметрами системы. Одной из таких задач является расчет давления идеального газа на стенки сосуда на основе молекулярно-кинетических представлений. Давление является результатом удара молекул о стенки сосуда.

Представим себе сосуд в виде куба с длиной ребра Δl, в котором беспорядочно движутся п молекул идеального газа. Масса каждой молекулы т₀. Ввиду полной беспорядочности движения, можно считать, что n׳ = п молекул движутся между передней и задней стенками, п – между верхней и нижней и п – между правой и левой . Одна из молекул, подлетая перпендикулярно к передней стенке со скоростью υ, ударяется о неё и упруго отскакивает назад со скоростью - υ. Её импульс меняется на величину:

Δp = - m₀ υ – ( +m₀ υ) = – 2m₀ υ .

Это изменение обусловлено действием на молекулу со стороны стенки силы f ′. По второму закону Ньютона f ′^. δ t = Δ p, где δ t – продолжительность удара. По третьему закону Ньютона сила f = - f ′ будет действовать на стенку со стороны молекулы. Молекула, отскочив от передней стенки, полетит к задней и вернётся к передней стенке через время . Заменим силу f силой < f >, такой, что f δ t = < f >Δt = 2 m₀ υ. Тогда

< f > = .

Это среднее по времени значение силы удара одной молекулы о переднюю

стенку. Так как число молекул, движущихся между передней и задней

стенками n׳ = п , то сила, действующая со стороны этих молекул на переднюю стенку, будет равна:

Обозначим 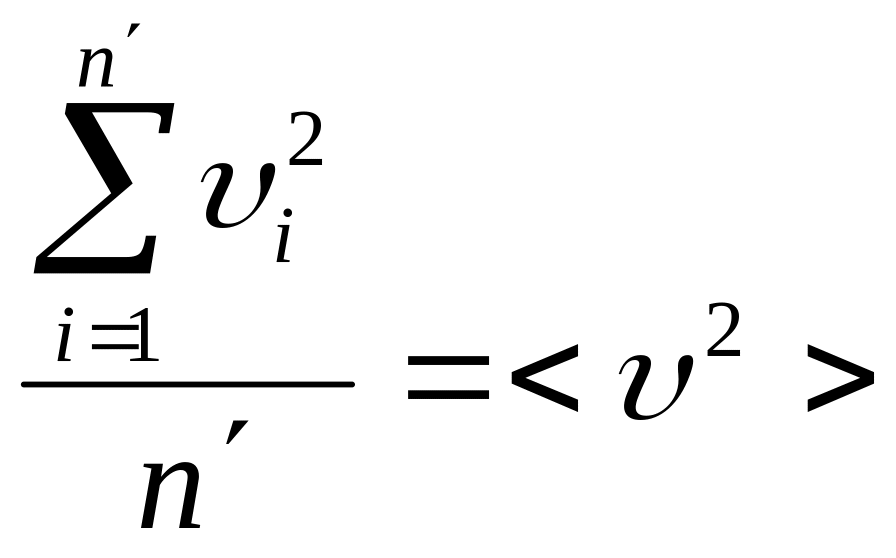– это среднее значение квадратов скоростей молекул или квадрат средней квадратичной скорости . Итак, получим:

Так как р = то

,

. (4.7)

Уравнение (4.7) - основное уравнение молекулярно-кинетической теории. Таким образом, давление р, оказываемое газом на стенки сосуда, определяется: числом молекул n₀ в единице объема, массой моле­кул т₀ и средним значением квадратов их скоростей < υ² >. Формуле (4.7) можно придать иной вид, поделив и помножив ее правую часть на 2, тогда

. (4.8)

Учитывая, что средняя кинетическая энергия поступательного движения одной молекулы идеального газа , основное уравнение МКТ

можно также записать в виде:

. (4.9)

Мы получили связь между давлением газа (макропараметр) и средней квадратичной скоростью одной молекулы (4.7) или средней кинетической энергией поступательного движения одной молекулы (4.9) (микропараметры).

В формуле (4.9) n₀w_пост - средняя кинетическая энергия поступательного движения молекул в единице объема, т.е. объемная плотность энергии:

n₀w_пост = W₀,

и

p = W₀,

таким образом, давление связано с объемными, энергетическими характеристиками газа. Учтём, что т₀ п₀ = ρ - плотность газа, тогда основное

уравнение молекулярно-кинетической теории (4.7) можно записать ещё и в

таком виде:

. (4.10)

Уравнения (4.7), (4.9), (4.10) – разные формы записи основного уравнения молекулярно-кинетической теории.