3.9 Элементы механики жидкостей и газов

3.9.1 Основные понятия

Молекулы газа, совершая беспорядочное, хаотическое дви­жение, не связаны или слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударений стре­мятся разлететься во все стороны, заполняя весь предоставленный им объем, т.е. объем газа определяется объемом того сосуда, кото­рый газ занимает.

Как и газ, жидкость принимает форму того сосуда, в кото­рый она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.

Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинако­выми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика — раздел механики, изучающий равновесие и дви­жение жидкостей и газов, их взаимодействие между собой и обтекаемыми или твердыми телами — использует единый подход к изучению жидкостей и газов.

В механике отвлекаются от молекулярного строения жидкостей и газов, рассматривая их как сплош­ную среду, непрерывно распределённую в

занимаемом ими объёме.

Плотность жидкости практически не зависит от давления и во многих задачах можно пользоваться понятием несжимаемой жид­кости — жидкости, плотность которой всюду одинакова (при Т = const) и не из­меняется со временем. Плотность газов, вообще говоря, не постоянна. При Т = const плотность газов пропорциональна давлению. Однако, как показывают расчёты, при не слишком больших скоростях течения υ сжимаемостью газа можно пренебречь. Например, для воздуха при υ ≤ 100 м/с пренебрежение сжимаемостью приводит к ошибке ≤ 5%. Таким образом, в ряде задач можно пользоваться понятием несжимаемого газа.

Движение жидкостей или газов называется течением, а совокупность частиц движущейся сплошной среды — потоком.

Д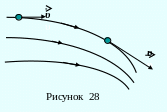 ля кинематического описания сплошной среды обычно используют метод Эйлера: задаётся поле скоростей , т.е. зависимость скорости от радиус – вектора рассматриваемой точки в потоке и от времени: = f ( , t ). Течение потока называют стационарным течением (установившимся), если скорость в каждой точке потока не зависит от времени.

В поле скоростей можно провести линии, касательные к которым в каждой точке совпадают с направлением скорости частицы потока в этой точке. Такие линии называются линиями тока (рисунок 28). Линии тока проводят так, что густота их больше там, где больше скорость потока.

Часть жидкости (газа), ограниченная линиями тока, называется трубкой тока. При установившемся течении трубки тока не изменяются со временем. Частицы среды движутся так, что каждая из них всё время остаётся в пределах определённой струйки.

В реальных жидкостях и газах течение осложняется тем, что между отдельными слоями потока имеется внутреннее трение. Однако в ряде случаев внутренним трением можно пренебречь. Жидкость (газ), в котором отсутствует внутреннее трение, называется идеальной жидкостью (газом). В реальных условиях это справедливо при течении жидкости в коротких и широких трубах и каналах, а также при обтекании жидкостью твёрдых тел, имеющих удобообтекаемую форму. Внутреннее трение проявляется лишь в сравнительно тонком приграничном слое жидкости, непосредственно прилегающем к поверхности труб, каналов, обтекаемых тел. Это приближение тем более точно, чем меньше вязкость жидкостей (например, вода, спирт и др. в обычных условиях). Вязкость газов вообще незначительна.

3.9.2 Давление внутри жидкости (газа)

Физическая величина, равная силе, действующей со стороны жидкости (газа) на единицу площади по направлению нормали к этой площади, называется давлением жидкости (газа):

p = F /ΔS.

Единица давления – паскаль (Па): 1 Па = 1 Н/м².

Б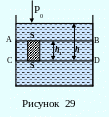 . Паскаль (1623-1662) установил, что давление на жидкость или газы передается ими равномерно во все сто­роны (закон Паскаля).

Для несжимаемой жидкости плотность постоянна по всему объёму. При поперечном сечении S столба жидкости, его высоте h и плотности  сила давления на слой CD, находящийся на глубине h, (рисунок 29) находится по формуле:

F =  g h S, (3.96)

поэтому давление на нижнее основание

(3.97)

Давление  g h называется гидростатическим давлением. Таким образом, гидростатическое давление линейно возрастает с высотой столба жидкости.

Согласно формуле (3.96) сила давления на нижние слои жид­кости СD будет больше, чем на верхние АВ (рисунок 29). Поэтому, если тело погрузить в жидкость или газы, то на него будет действовать выталкивающая сила, определяемая законом Архимеда:

на тело, погруженное в жидкость (газ), дей­ствует вы­талкивающая сила, равная весу жидкости (газа) вытесненной этим телом:

,

где — плотность жидкости (газа), V — объем погруженного в жид­кость (газ) тела.