Свойства линейных операций: Везде далее матрицы , и - матрицы одного размера.

1. Ассоциативность 

2. , где   - нулевая матрица соответствующего размера.

3. 

4. Коммутативность

5. Дистрибутивность 

6. 

7. 

Произведение двух матриц

Произведением матрицы на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и 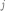-ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .

Свойства произведения матриц:

1. Ассоциативность

2. Ассоциативность по умножению

3. Дистрибутивность ,

4. Умножение на единичную матрицу

5. В общем случае умножение матриц не коммутативно, т.е .

6.

Транспонирование матриц

Транспонирование матрицы – это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Свойства транспонирования матриц:

1. 

2. 

3. 

4. 

3.Определители матриц, их свойства.

Понятие определителя матрицы

Квадратной матрице n –го порядка ставиться в

соответствие число , называемое определителем матрицы или детерминантом.

Свойства определителей:

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1° При транспонировании квадратной матрицы её определитель не меняется:

2° Общий множитель в строке можно выносить за знак определителя.

3° То есть, если квадратная матрица    -го порядка умножается на некоторое ненулевое число  , то определитель полученной матрицы равен произведению определителя исходной матрицы   на число   в степени, равной порядку матриц.

4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5° Если две строки определителя поменять местами, то определитель поменяет знак.

6° Определитель с двумя равными строками равен нулю.

7°    Определитель с двумя пропорциональными строками равен нулю.

8°    Определитель, содержащий нулевую строку, равен нулю.

9°    Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

10°    Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

11°    Определитель произведения матриц равен произведению определителей:

4.Разложение определителя по элементам любой строки, столбца.

  Рассмотрим квадратную матрицу  A  n-го порядка.        Выберем  i,j-ый элемент этой матрицы и вычеркнем  i-ую строку и  j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом  M_i j:

Алгебраическое дополнение  A_i,j  элемента  a_i j определяется формулой

Теорема о разложении определителя по элементам строки. Определитель матрицы  A  равен сумме произведений элементов строки на их алгебраические дополнения:

Теорема о разложении определителя по элементам столбца. Определитель матрицы  A  равен сумме произведений элементов столбца на их алгебраические дополнения: