9. Минимизация методом Квайна - МакКласски.

На первом этапе в методе Квайна попарно сравнивают все импликанты, входящие в СДНФ, в целях выявления возможности поглощения какой-то переменной на основе закона склеивания:

.

Процедура продолжается до тех пор, пока не останется ни одного члена, допускающего поглощение с другим термом. В результате получают некоторое количество простых импликант. Дизъюнкция этих импликант является сокращенной ДНФ.

На втором этапе строится таблица покрытий.В строках этой таблицы указываются найденные простые импликанты, а в столбцах - термы исходного выражения функции. Клетки таблицы отмечаются, если простая импликанта входит в состав какого-либо терма. В итоге минимизация булевой функции сводится к тому, чтобы найти такое минимальное количество простых импликант, которые покрывают все столбцы. В результате получают тупиковую ДНФ.

Недостаток метода-необходимость попарного сравнении всех конъюнктивных термов на первом этапе при нахождении простых импликант. С ростом числа исходных термов увеличивается количество попарных сравнений, что усложняет решение задачи минимизации.

Метод Квайна с применением п-мерных кубов

Данный метод устраняет недостаток предыдущего метода, т.е. устраняет необходимость попарного сравнения всех термов на первом этапе при нахождении простых импликант. Для этого строится п-мерный куб, по которому визуально можно определить те конъюнктивные термы, склеивание которых порождают простые импликанты.

При решении задачи минимизации булевой функции удобно вместо конъюнктивных термов использовать, соответствующие им, двоичные наборы.

Метод Квайна - Мак-Класки

Метод Квайна - Мак-Класки представляет собой предыдущий метод, но без геометрического построения п - мерных кубов: кубы присутствуют, но абстрактно.

Метод основан на кубическом представлении конъюнктивных термов ДНФ с предварительным разбиением кубов на подгруппы, определяемые одинаковым числом единиц. Разбиение дает возможность сравнивать кубы только соседних по числу единиц групп для уменьшения количества переборов.

В итеративной процедуре минимизации попарное сравнение можно производить только между соседними группами.

Нахождение простых импликат на первом этапе:

1. Все исходные конъюнктивные термы записываются в виде их двоичных наборов.

2. Все наборы разбиваются на непересекающиеся группы по числу единиц. Условие образования r-куба - наличие расхождения в (r-1)-кубах только по одной координате в одном двоичном разряде и наличие общих независимых координат.

3. В i-группу включают все двоичные наборы, имеющие в своей записи i единиц.

4. Попарное сравнение производится только между соседними по номеру группами. Группы, которые различаются в двух разрядах и более, не имеет смысла сравнивать.

10. Графические методы минимизации: Диаграммы Вейча.

" Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча. Для булевой функции двух переменных диаграмма Вейча имеет вид (табл. 4.4.1).

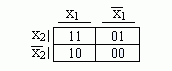
Каждая клетка диаграммы соответствует набору переменных булевой функции в ее таблице истинности. В (табл. 4.4.1) это соответствие показано, В клетке диаграммы Вейча ставится единица, если булева функция принимает единичное значение на соответствующем наборе. Нулевые значения булевой функции в диаграмме Вейча не ставятся. Для булевой функции трех переменных диаграмма Вейча имеет следующий вид (табл. 4.4.2).

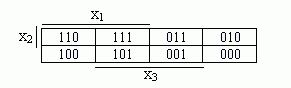
Добавление к ней еще такой же таблицы дает диаграмму для функции 4-х переменных (табл. 4.4.3).

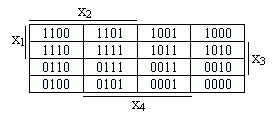
Таким же образом, т. е. приписыванием еще одной диаграммы 3-х переменных к только что рассмотренной, можно получить диаграмму для функции 5-ти переменных и т. д., однако диаграммы для функций с числом переменных больше 4-х используются редко. Для приведенных диаграмм характерно следующее:

• каждой клетке диаграммы соответствует свой набор;

• соседние наборы расположены рядом в строке либо в столбце.

Соседними наборами называются наборы, отличающиеся одной компонентой. Напомним, что конституенты, соответствующие таким наборам, склеиваются (см. метод Квайна- Мак-Класки). Например, для функции, заданной табл. 9.22,

конституенты, соответствующие паре единиц в левой части таблицы, склеиваются и порождают элементарное произведение из 2-х букв:

х₁х₂/х₃ v x₁x₂x ₃ = x₁x₂

О паре единиц в правой части диаграммы можно сказать то же самое:

/х₁х₂/х₃ v /x₁/x₂/x ₃ = /x₁/x₃

Отметим, что получающееся элементарное произведение легко определить сразу по диаграмме: это произведение переменных, принимающих одно и то же значение в обеих клетках. Еще одно важное замечание: столбцы, расположенные по краям диаграммы, тоже считаются соседними. Для нашего примера это означает, что имеет место еще одно склеивание, в результате которого, следуя указанному правилу, получаем элементарное произведение x₂/x₃ Из рассмотренных ранее методов нам известно, что возможно дальнейшее склеивание получаемых элементарных произведений. На диаграммах Вейча они тоже располагаются рядом. Общее правило склеивания на диаграммах Вейча можно сформулировать следующим образом: склеиванию подлежат прямоугольные конфигурации, заполненные единицами и содержащие число клеток, являющееся степенью 2. Получающееся новое элементарное произведение определяется как произведение переменных, не меняющих своего значения на всех склеиваемых наборах. Число m оставшихся переменных в элементарном произведении определяется легко:

m = n - log₂M

где n - число переменных функции, М - число склеиваемых наборов. Метод широко используется на практике, благодаря простоте и удобству. После небольшой тренировки достигается элементарный навык определения минимальной ДНФ по диаграмме "с первого взгляда". Минимизация булевой функции заключается в нахождении минимального накрытия всех единиц диаграммы Вейча блоками из единиц (указанной конфигурации), расположенных в соседних клетках диаграммы. При этом всегда считается, что левый край диаграммы Bейча 4-х переменных примыкает к ее правому краю, а верхний oкрай диаграммы примыкает к нижнему ее краю. После получения минимального накрытия всех единиц диаграммы Вейча, минимальная ДНФ булевой функции записывается как дизъюнкция элементарных конъюнкций, соответствующих выделенным блокам единиц в диаграмме. Рассмотрим несколько примеров. Пример. Булева функция f имеет следующую СДНФ:

f=х₁х₂х₃ v х₁/х₂х₃ v /х₁/х₂/х₃ v /х₁/х₂/х₃ v х₁х₂/х₃.

Найти минимальную ДНФ с помощью диаграммы Вейча. Диаграмма Вейча, соответствующая функции f, представлена в табл. 4.4.5. Минимальное накрытие всех единиц диаграммы возможно только блоками по две единицы. Каждому такому блоку соответствует своя конъюнкция, как показано в табл. 4.4.5.

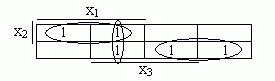
Следовательно, минимальная ДНФ функции имеет вид:

f = х₁х₂ v /х₁/х₂ v х₁х₃.

Пример.

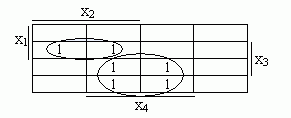
f₁=х₁х₂х₃ v /х₁х₄.

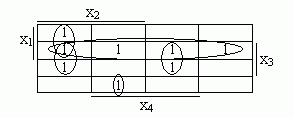
f₂=х₁х₂х₄ v х₂х₃/х₄ v х₁х₃ v /х₂х₃х₄ v х₁х₂х₃x₄.

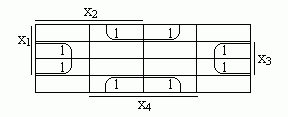
f₃=х₃/х₄ v /х₃х₄.

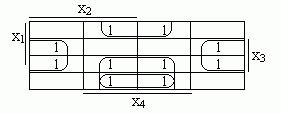
f₄=/х₃х₄ v /х₁х₄ v х₁х₃/х₄.

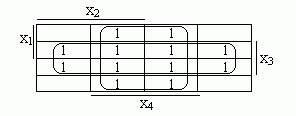
f₅=х₃ v х₄.

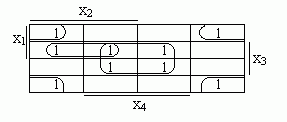
f₆=х₃х₄ v /х₃/х₄ v х₁х₂х₃. " 

Вопрос № 11 Машины Тьюринга и Неймана. Состояние и алфавит

*Про алфавит и состояние описывается в контексте машин, более конкретной инфы не нашел

Хотя машина Тьюринга (МТ) не стала реально действующим устройством, она до настоящего времени постоянно используется в качестве основной модели для выяснения сущности таких понятий, как "вычислительный процесс", "алгоритм", а также для выяснения связи между алгоритмом и вычислительными машинами.

Основные положения машины Тьюринга

1. Машина Тьюринга имеет конечное число знаков si, образующих внешний алфавит, в котором кодируются сведения, подаваемые в МТ, а также вырабатываемые в ней. Среди знаков имеется пустой знак (s1), посылка которого в какую-либо ячейку стирает находившийся в ней знак и оставляет ее пустой.

В зависимости от поданной начальной информации  (содержащихся на ленте внешней памяти знаков) возможны два случая:

• после конечного числа тактов машина останавливается (имея информацию β), подавая сигнал об остановке. В этом случае МТ применима к информации  и перерабатывает ее в информацию β; 

• остановка никогда не наступает. В этом случае МТ не применима к начальной информации  .

В каждый момент обозревается лишь одна ячейка ленты (памяти). Переход может осуществляться лишь к соседней ячейке ( R – вправо, L–влево, N– нет перехода (остаться)). Переход к произвольной ячейке производится путем последовательного перебора всех ячеек, разделяющих текущую и необходимую ячейки. На каждом отдельном такте t команда предписывает только замену единственного знака si, хранящегося в обозреваемой ячейке, каким-либо другим знаком sj.