32. Теорема Роля, Лагранжа, Коши, их применение. Правило Лопиталя.

Теорема Роля.

Если функция непрерывна на отрезке и дифференцируема в нутрии его, а на концах данного отрезка функция принимает одинаковое значение ( т. е. , тогда найдется хотя бы одна точка к которой ( произведение обращенное в нуль)

Теорема Лагранжа.

Если непрерывна на отрезке и дифференцируемый в него, то найдется хотя бы одна точка , что

Теорема Коши.

Если функция и непрерывна на отрезке и дифференциал в нутрии его, то найдется хотя бы одна точка , что выполняется ( где )

Правило Лопиталя.

Правила лопиталя – это способ раскрытия неопределенности вида .

Теорема 1.

Пусть функция и непрерывны и дифференциалы в окрестности точки и обращаются в этой точке в нуль. Тогда

Теорема 2.

Пусть функция и непрерывны и дифференцируемы в точке , кроме того предел , кроме того, тогда справедлива.

33. Условия монотонности функции. Экстремум, необходимое и достаточное условия существования экстремума в точке. Исследование функций на экстремум с помощью второй производной.

Функция возрастает на интервале где производная больше нуля , а убывает где .

На оси откладываем все критические точки и точки области ОДЗ и на каждом из интервалов определяем знак производной.

Экстремум.

Точка называется точкой максимума (минимума) функции если существует такая окрестность в точке в каждой точки которой выполняется неравенство.

Экстремумом функции называется максимальное / минимальное значение функции.

Необходимое условие экстремума:

Если дифференцируемая функция имеет экстремум в точке то производная в этой точке равна нулю

Замечание: Однако существуют функции в которых в точках экстремума не существует производной. Точки в которых производная равна нулю или не существует называется критическими.

34. Наибольшее и наименьшее значение функции на отрезке. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты кривой. Общая схема исследования функции и построения графика.

Точки перегиба и интервалы выпуклости.

Точка называется точкой перегиба функции если

Функция называется выпуклой в верх на интервале , если в каждой точке этого интервала вторая производная меньше нуля ; выпуклой в низ /

Выпуклая вниз (касательная к данной кривой ниже самой кривой)

Касательная выше выпуклая в верх

Найти асимптоты.

Асимптоты прямой называется прямая, расстояния до которой от точки лежащей на кривой, стремиться к нулю, при неограниченном удалении от начала координат.

Асимптоты бывают: вертикальные, наклонные (могут оказаться горизонтальными)

1. Прямая называется вертикальной функцией асимптотой

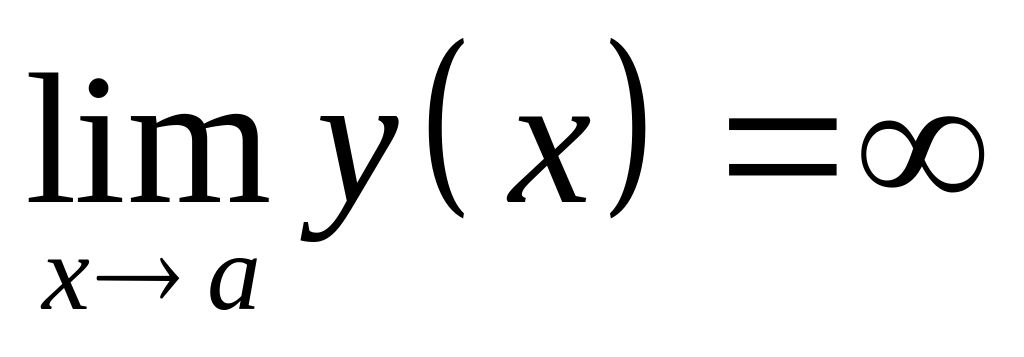
2. Наклонная асимптота имеет вид

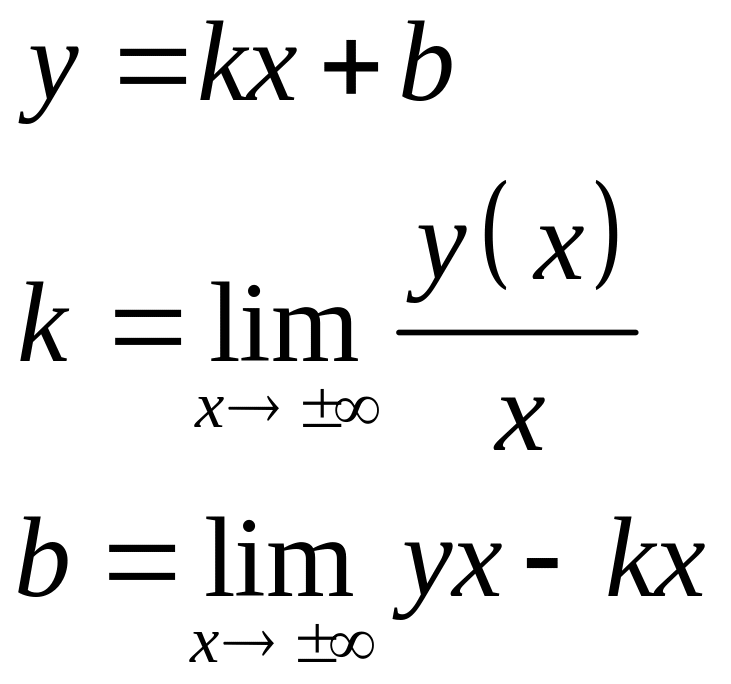
Общая схема исследования.

1. Найти ОДЗ

2. Проверить функцию на четность или нечетность

3. Если возможно найти точки пересечения с осями координат

4. Найти экстремумы функции

5. Найти интервалы монотонности функции

6. Найти точки перегиба графика функции и интервалы выпуклости вогнутости

7. найти асимптоты графика функции.

19. Линии второго порядка.

Эллипс.

Эллипсом называется геометрическое место точек плоскости для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная равная , причем , где - расстояние между фокусами.

где

Эксцентриситет равен

Он характерезует степень приплюстности эллипса.

Чем меньше Е тем будет менее сплющен эллипс. Если Е=0 то эллипс превратиться в окружность..

Формулы для эллипса:

Прямые - называют директрисами.

Для эллипса Е может быть вычислен по формуле , где r – расстояние от произвольной точки до ближайшего фокуса, d – расстояние от тойже точки до соответсвующей этому фокусу директрисы.

Гипербола

Гиперболой называется геометрическое место точек плоскости для которых разность расстояний от двух фиксированных точек плоскости называемых фокусами , есть величина постоянная, равная 2а, при чем 2a<2C, где 2с – расстояние между фокусами

- каноническое уравнение.

вычисляется по формуле и он также характерезует форму гиперболы: чем меньше Е тем больше вытянут основной прямоугольник.

- асимптоты.

- директрисы.

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).

Каноническое уравнение параболы.

Нетрудно показать, что график квадратного трехчлена  , где  , B и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.