Предел функции при

Определение: Число А называется предел при если , что при всех x для которых будет справедливо

25. Бесконечно малые и бесконечно большие функции. Первый и второй замечательный предел.

Функция называется бесконечно большой при если (тоесть . Функция называется бесконечно малая при если (т.е. )

Первый замечательный предел.

Второй замечательный предел.

или

26. Эквивалентные бесконечно малые функции.

Для того чтобы сравнивать между собой бесконечно малые функции рассматривают их отношение.

Пусть и - бесконечно малые при т.е.

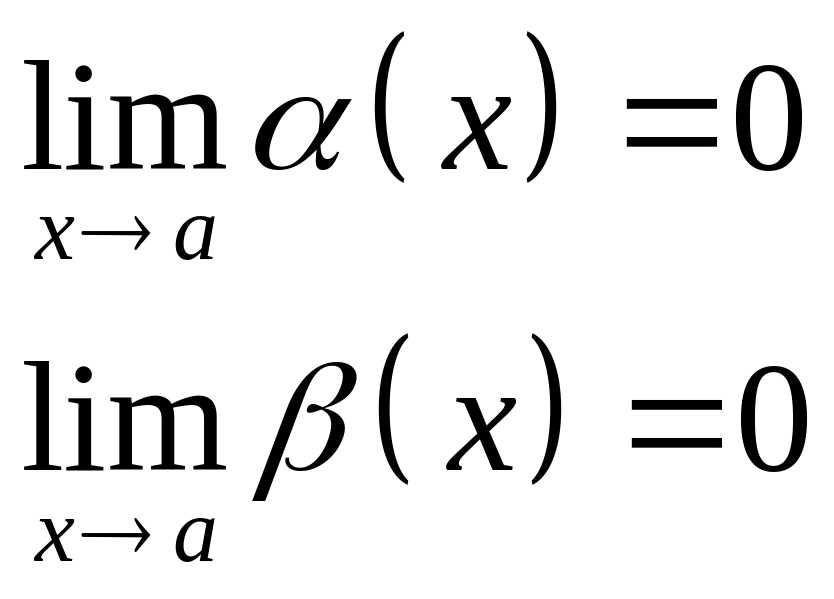
1. Если 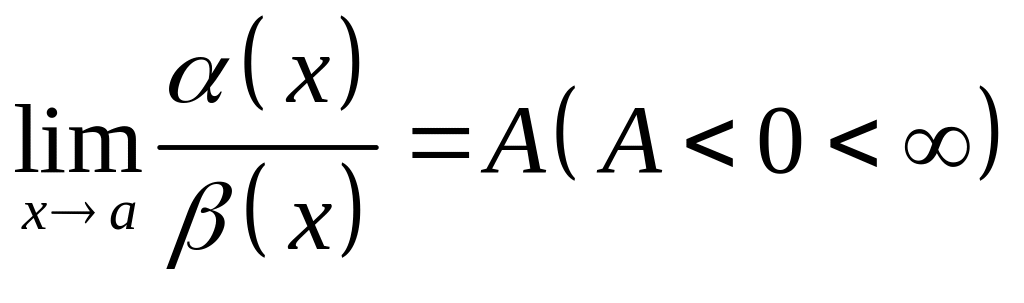то и называют бесконечно малыми одного порядка.

2. Если то называют бесконечно малыми.

3. Если то называют б.м. более низкого порядка чем

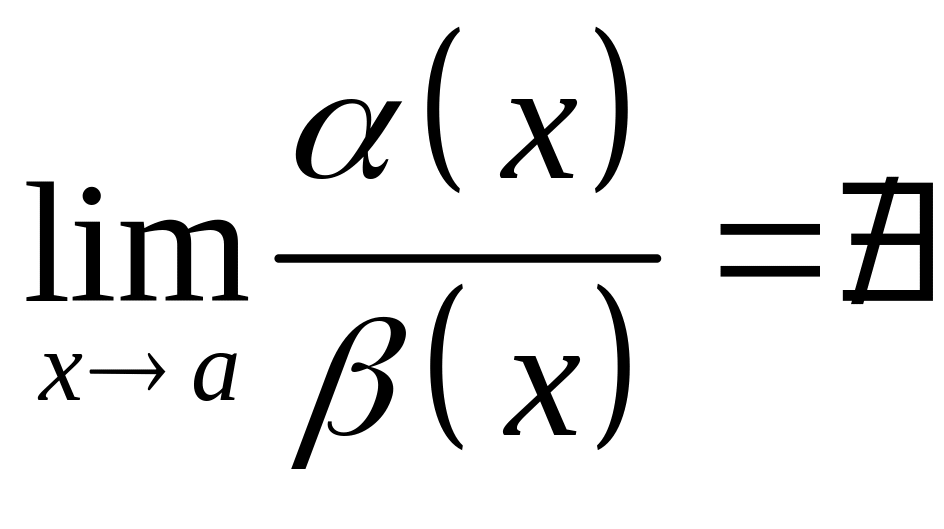4. то и называют несравнимыми бесконечно малыми.

Если то и называют эквивалентами б.м. при

Теорема: Предел отношения двух бесконечно малых функций не измениться, если каждую или одну из них заменить эквивалентной бесконечно малой.

Пример:

27. Непрерывность функции в точке. Точки разрыва и их классификация.

Пусть функция определена в точке и некоторой ее окрестности. Функция называеться непрерывной в точке если выполнено 3 условия.

1. Функция определена в точке

2. Функция имеет придел при

3. 

Замечание:

Для нахождения предела непрерывныой функции можно перейти к пределу под знаком функции.

Функция непрерывна на , если она не прерывна в каждой точке этого интервала.

Точки разрыва и их классификация.

Точками разрыва называют такие значения при которых не выполняются хотябы одно из условий определения непрерывности функции.

Примеры:

в точке =-3 функция не вычисляется разрыв II рода

разрыв I рода

28. Основные теоремы о непрерывных функциях.

Теорема 1.

Сумма произведения и частное двух непрерывных функций есть функция непрерывная ( для частного за исключением точек в которых осуществляется деление на 0)

Теорема 2.

Все элементарные функции непрерывны при всех значениях для которых они определены

Теорема 3. (Вейерштрасса)

Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значения.

Теорема 4. (Больцано – коши)

Если функция непрерывна на отрезке и принимает на его концах неравные значения, то она принимает на этом отрезке и все промежуточные значения.

29. Производная функция, ее геометрический смысл.

Производная функции в точке X называется предел отношения приращения функции и приращению аргумента, когда приращение аргумента стремиться к 0

Геометрический смысл производной.

- угол между осью Ox и хордой при

где - угол между осью Ox и касательной в точке x.

Правила дифференцирования функций.

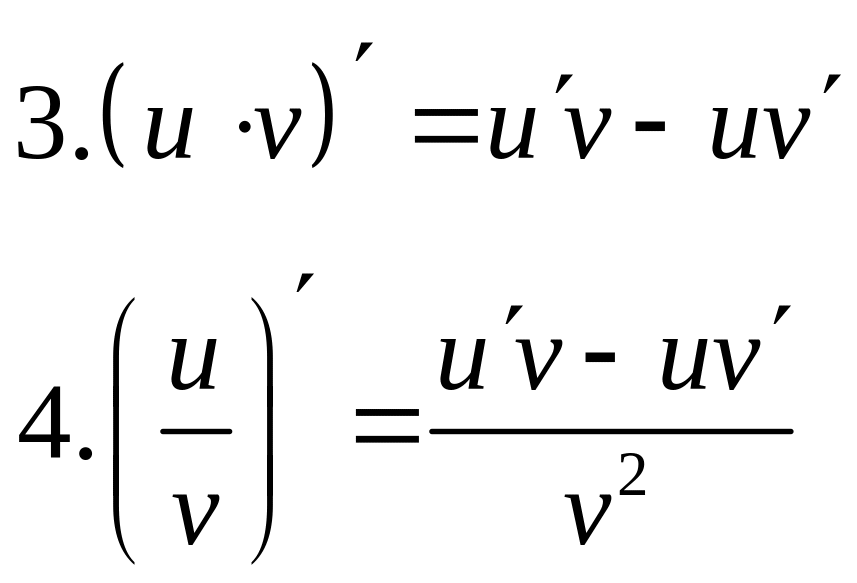
Таблица производных.

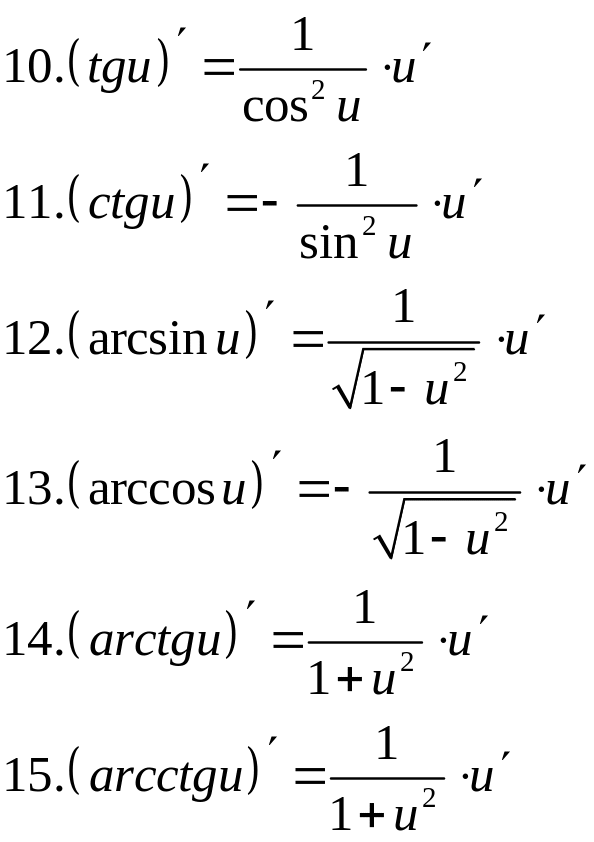
30. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Производные высших порядков.

Производная функции заданная параметрически.

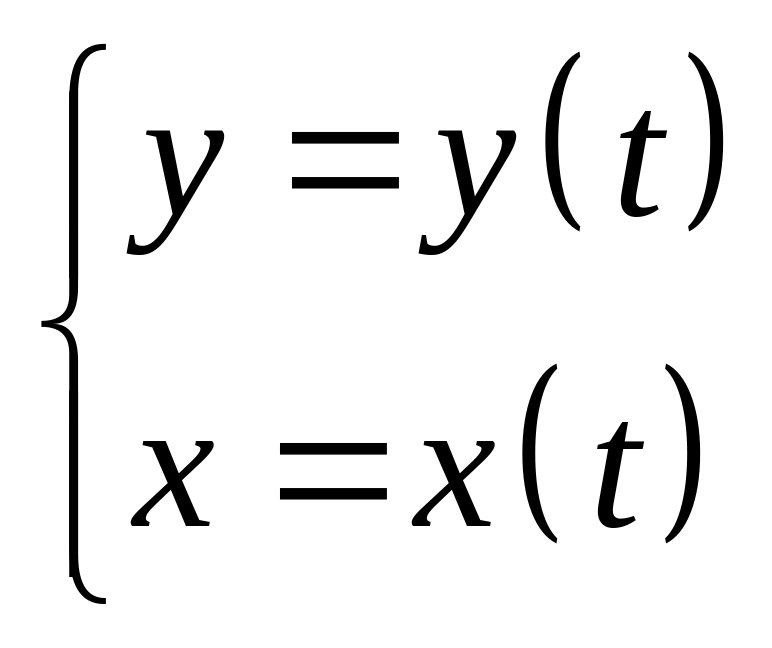
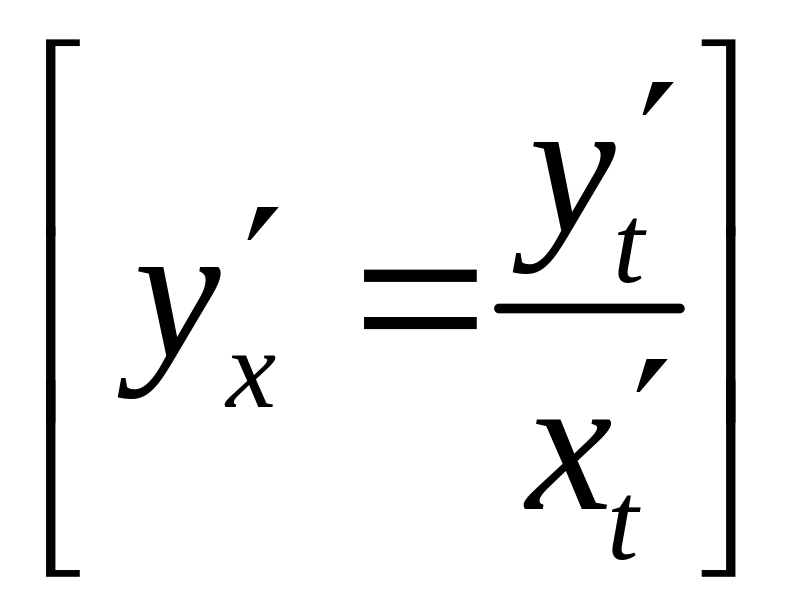
Производная функции заданная неявно.

Для нахождения производной достаточно продифференцировать это уравнение по Х, рассматривая при этом У как функцию от Х. Полученное выражение затем требуется разрешить .

Пример.

Логарифмическое дифференцирование.

Данное дифференцирование подходит для степенно показательных функций т. е. функций вида

Пример.

Производные высших порядков.

Пусть задана функция . Тогда называется производной первого порядка. А выражение обозначается как и называется производной второго порядка. Аналогично /

Замечание. Обозначение производной энного порядка

Производная высших порядков от функции заданной параметрически.

Производная высших порядков функции заданных неявно.

В процессе построения производной второго порядка не явно заданной функции начинается с нахождения в явном виде. Это уравнение дифференцируем по Х в результате получаем выражение , через . Далее в полученном выражении остается только заменить через X и Y

3. комплексные числа.

;

- минимальная единица

(при )

- модуль комплексного числа

- аргумент комплексного числа

Действия с комплексными числами.

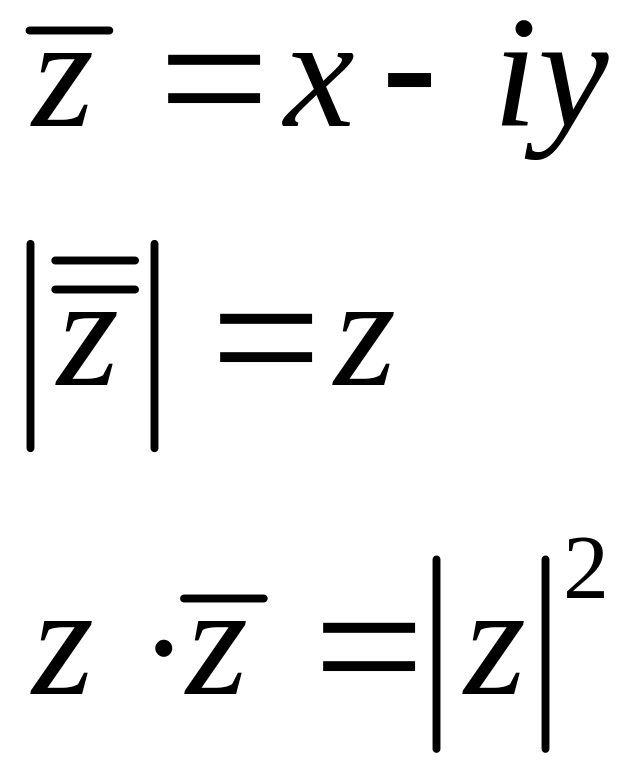
Формы записи комплексных чисел

31. Дифференциал функции и его свойства. Применение дифференциала в приближенных вычислениях. Дифференциалы высших порядков.

Дифференциал функции называется главная часть её приращения, равная произведению производной функции на приращения аргумента и обозначается

Дифференциал независимой переменной равен её приращению.

- дифференциал функции.

Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Приближенные вычисления

Данные вычисления основываются на том что приращение функции приближенно равно дифференциалу функции.

Дифференциалы высших порядков.

Пусть задана дифференцируемая на некотором отрезке тогда её дифференциал имеет вид: - называется дифференциал первого порядка. Дифференциал второго порядка называется дифференциал от дифференциала первого порядка и обозначается