20. Уравнение плоскости в пространстве.

1. Общее уравнение плоскости.

, где A,B,C,D – числа.

Частные случаи.

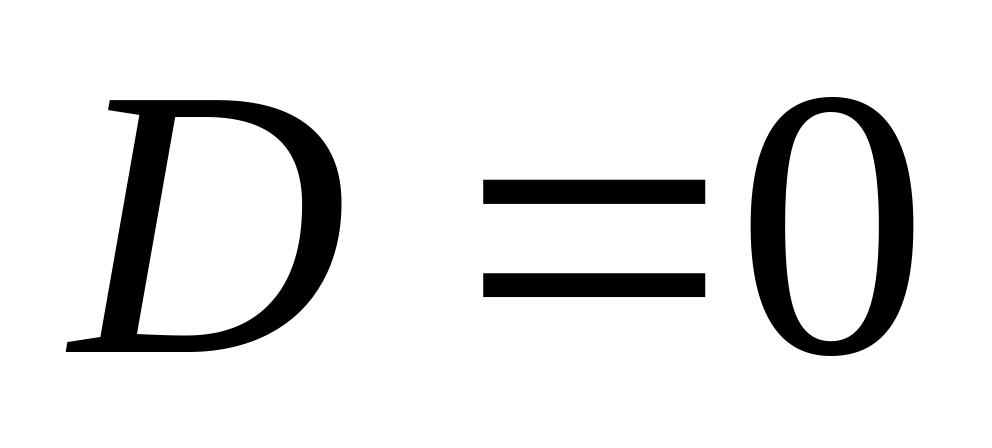
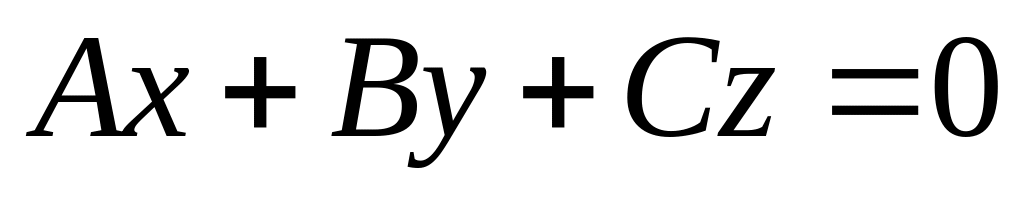• ,плоскость проходит через начало координат.

• плоскость // Oz (ось Oz не пересекает)

• плоскость // Oy

• плоскость // Ox

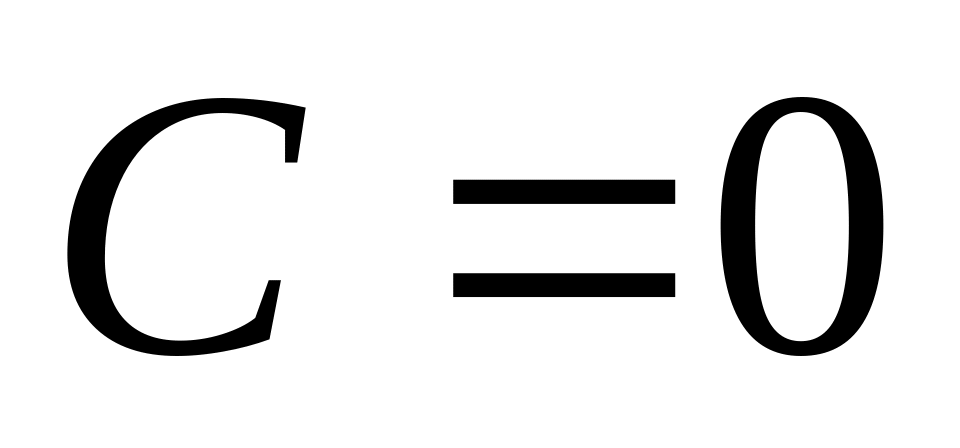
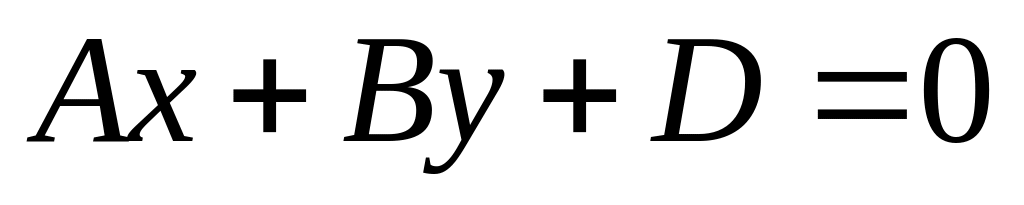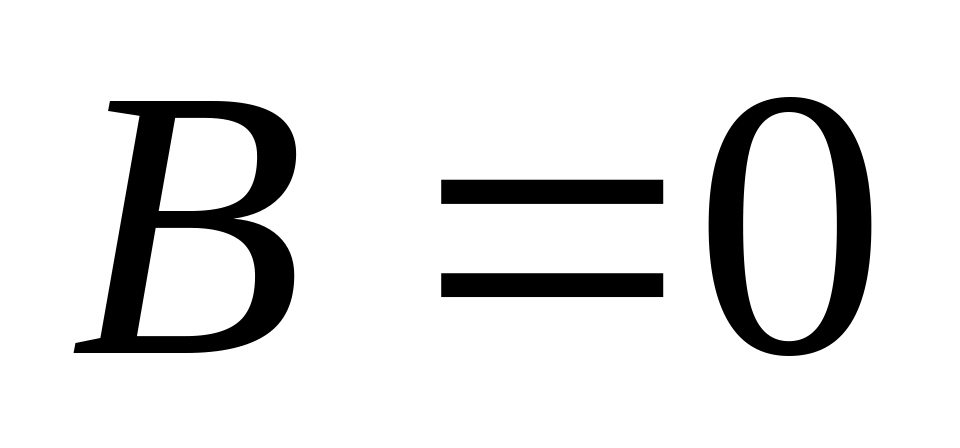
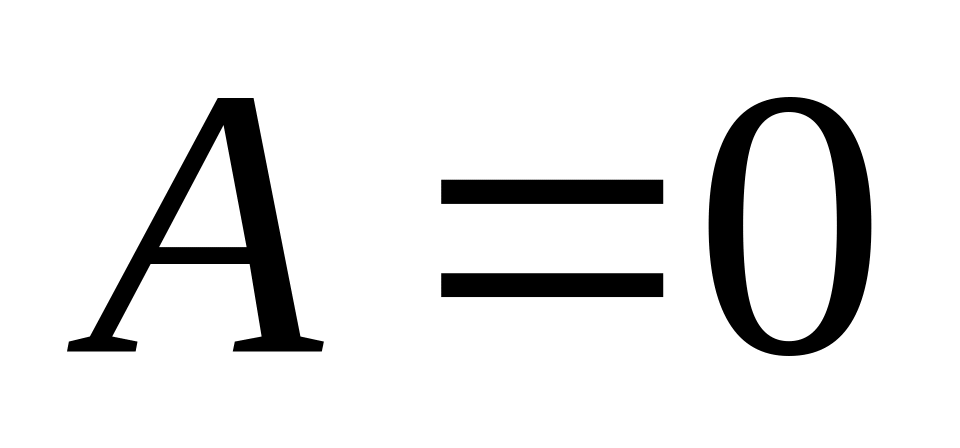
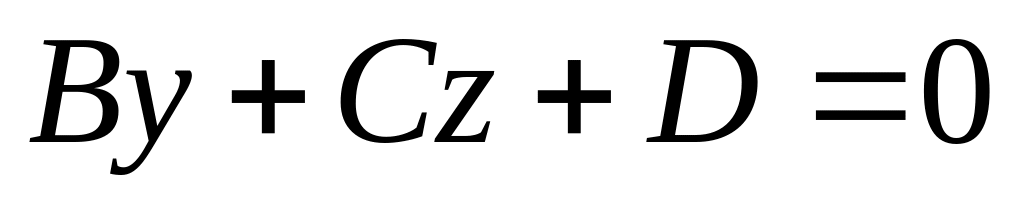• плоскость // на плоскости Oy

2. Уравнение проходящее через данную точку перпендикулярна заданному вектору.

3. Уравнение плоскости проходящее через 3 заданные точки.

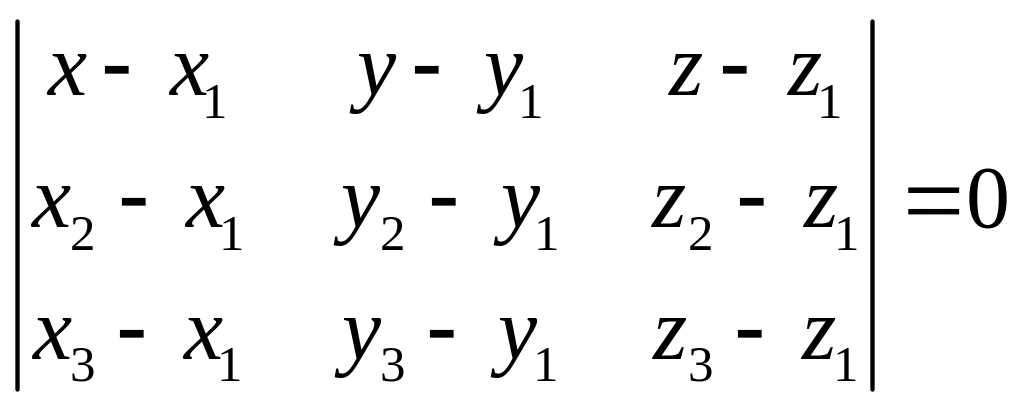
4. Уравнение плоскости в отрезках

5. Нормальное уравнение.

где

6. переход от общего уравнения к общему.

Умножим общее уравнение на и получим нормальное уравнение 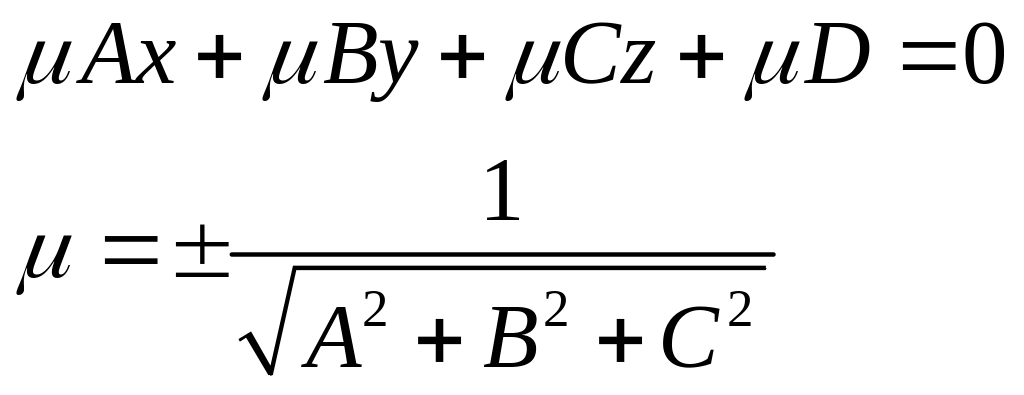где знак противоположен знаку D

7. Расстояние от точки до плоскости

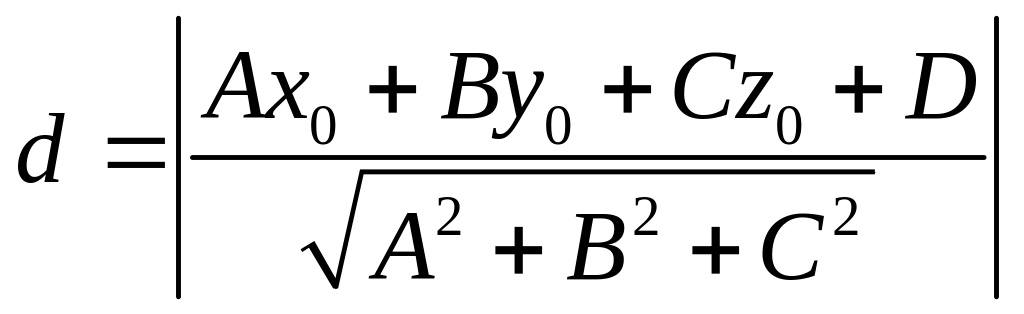
8. Угол между двумя плоскостями.

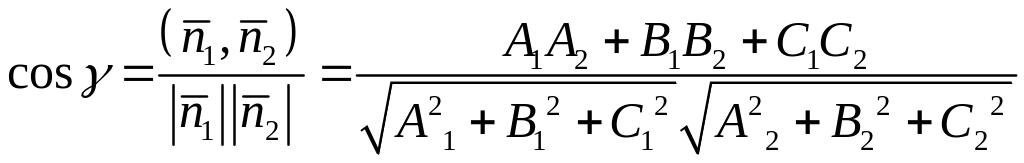
21. Уравнение прямой в пространстве.

1. Общее уравнение прямой.

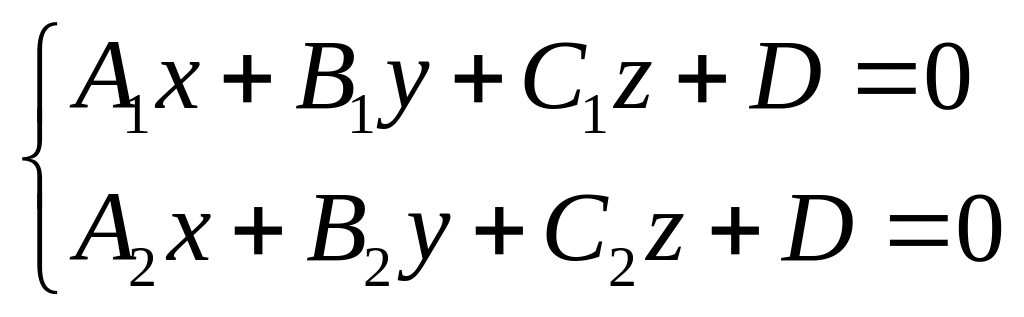
То есть прямая в пространстве получается как пересечение двух плоскостей.

2. Каноническое уравнение прямой ( уравнение прямой проходящей через заданную точку параллельно направляющему вектору)

3. Параметрическое уравнение прямой.

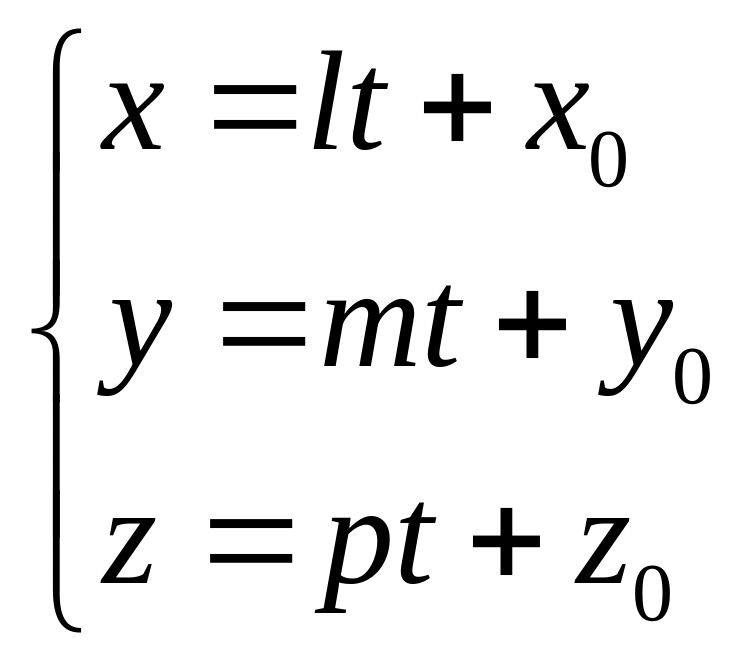t - коэфициэнт подобия

4. Уравнение прямой проходящие через две заданных точек.

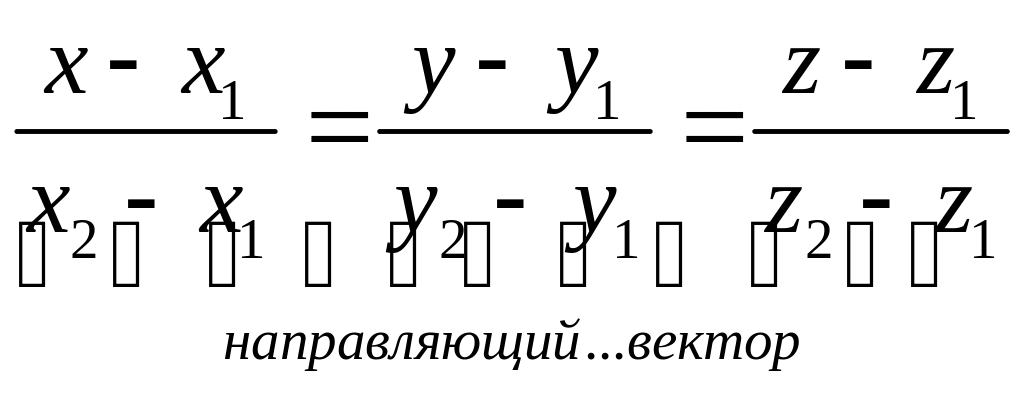
5. Переход от канонического уравнения к общему.

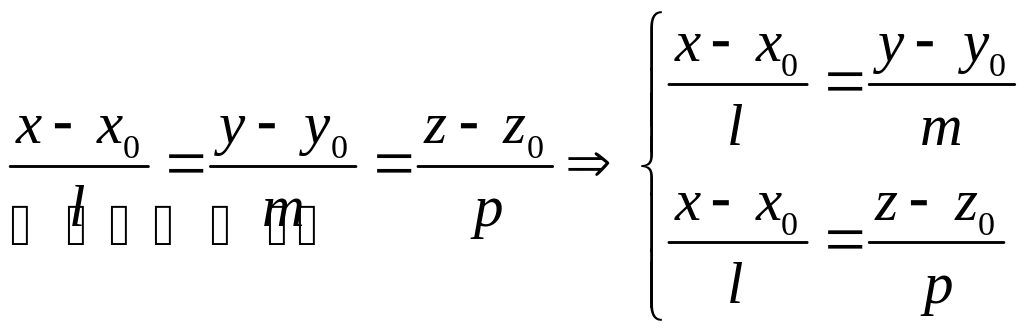
6. Переход от общего уравнения к общему.

Нужно найти точку на прямой направляющего вектора.

Точка на прямой находиться из решения системы ( нужно одну неизвестную приравнять к нулю) получаем точку

7. Угол между двумя прямыми.

Для того чтобы найти угол между двумя прямыми можно определить равный ему угол между направляющими векторами.

Угол между прямыми = углу между и

23. Числовая последовательность.

Под числовой последовательностью понимается функция заданная на множестве натуральных чисел. или .

Последовательность называется ограниченной если существует такое число , что для любого (номера) справедливо: .

Последовательность называется возрастающей (убывающей) если для любого номера n выполняется неравенства

Предел числовой последовательности.

Число А называется пределом последовательности , если для любого существует такой номер N, что при справедливо

Если предел существует то говорят, что последовательность сходиться к этому значению.

Теорема 1.

Если и и начиная с некоторого номера выполняется неравенство , то справедливо

Теорема 2.

Если и и начиная с некоторого номера выполняется , то справедливо

Всякая монотонная ограниченная последовательность имеет предел. Последовательность называется монотонной если она возрастает, убывает, не возрастает, не убывает.

24. Предел функции в точке.

Пусть функция определена в некоторой окрестности точки .

Определение: Число А называется пределом функции при , если для любого существует такое , что при справедливо .