
- •18.Уравнение прямой на плоскости.
- •1.Общее уравнение прямой.
- •4. Матрицы. Основные понятия. Действия над ними.
- •Обратная матрица.
- •Ранг матрицы.
- •9.Метод крамера.
- •2.Вычесляем определяемый определитель
- •3. Вычисляем корни уравнения
- •10. Решение произвольной слау.
- •Теорема Кронекера – капели
- •11. Метод Гаусса для решения слау. Однородная слау.
- •Однородная слау.
- •Свойства.
- •12. Элементы векторной алгебры.
- •13. Разложение вектора по ортам координатных осей. Направляющие косинусы. Действия над векторами заданными проекциями.
- •20. Уравнение плоскости в пространстве.
- •21. Уравнение прямой в пространстве.
- •1. Общее уравнение прямой.
- •23. Числовая последовательность.
- •Предел числовой последовательности.
- •24. Предел функции в точке.
- •Предел функции при
- •25. Бесконечно малые и бесконечно большие функции. Первый и второй замечательный предел.
- •26. Эквивалентные бесконечно малые функции.
- •27. Непрерывность функции в точке. Точки разрыва и их классификация.
- •Функция определена в точке
- •Функция имеет придел при
- •28. Основные теоремы о непрерывных функциях.
- •32. Теорема Роля, Лагранжа, Коши, их применение. Правило Лопиталя.
- •33. Условия монотонности функции. Экстремум, необходимое и достаточное условия существования экстремума в точке. Исследование функций на экстремум с помощью второй производной.
- •Экстремум.
- •Необходимое условие экстремума:
- •Понятие о рациональных функциях.
- •Разложение многочлена
13. Разложение вектора по ортам координатных осей. Направляющие косинусы. Действия над векторами заданными проекциями.
Система ортов (или базисная система векторов) - это система единичных векторов осей координат.
Орт
координатной оси ![]() обозначается
через
обозначается
через ![]() ,
оси
,
оси ![]() -
через
-
через ![]() ,
оси
,
оси ![]() -
через
-
через ![]() (рис.
1).
(рис.
1).

Для
любого вектора ![]() ,
который лежит в плоскости
,
который лежит в плоскости ![]() ,
имеет место следующее разложение:
,
имеет место следующее разложение:![]()
Если
вектор ![]() расположен
в пространстве, то разложение по ортам
координатных осей имеет вид:
расположен
в пространстве, то разложение по ортам
координатных осей имеет вид: ![]()
Направляющими
косинусами ![]() ,
, ![]() ,
, ![]() вектора
называются косинусы углов между вектором
и положительными направлениями
осей Ox, Oy и Oz соответственно.
вектора
называются косинусы углов между вектором
и положительными направлениями
осей Ox, Oy и Oz соответственно.
![]()
. Проекцией вектора на ось l () называется длина его компонентына осьl, взятая со знаком «плюс», если направление компоненты совпадает с направлением осиl, и со знаком «минус», если направление компоненты противоположно направлению осиl.
Если = 0, то полагают = 0.
Теорема 1. Проекция вектора на ось lравна произведению его модуля на косинус угла между этим вектором и осью l:
14. Скалярное произведение векторов и его свойства.
Определение. Скалярным
произведением двух векторов называется
число, равное произведению модулей этих
векторов на косинус угла между ними.![]() и
и
![]() называется число (скаляр) равное
называется число (скаляр) равное
![]() .
Скалярное произведение может быть
представлено через проекцию векторов.
.
Скалярное произведение может быть
представлено через проекцию векторов.

Свойства.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Выражение скалярного произведения через координаты.
![]()
Приложение.
Угол
между векторами. Угол между не нулевыми
векторами равен: работа постоянной силы.
работа постоянной силы.
![]()
15. Векторное произведение векторов и его свойства.
Векторным
произведением вектора
на вектор
называется такой вектор
![]() ,
что :
,
что :
![]()
Вектор
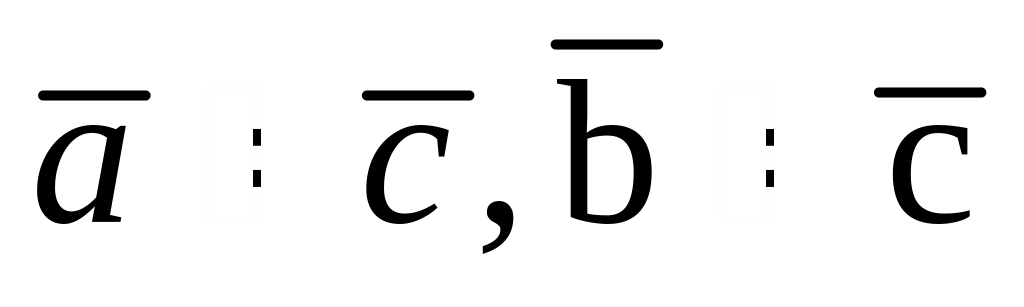
Длинна
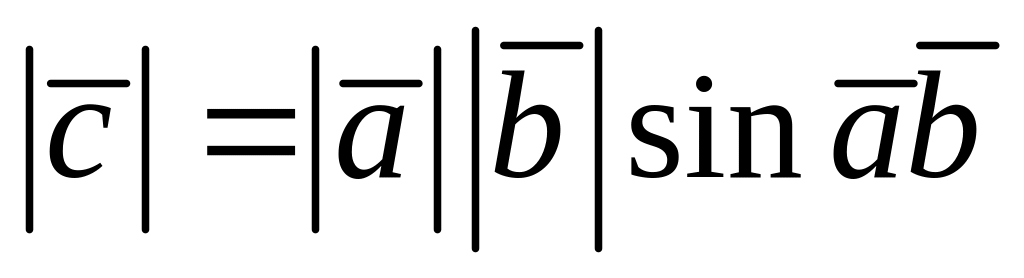
Векторы
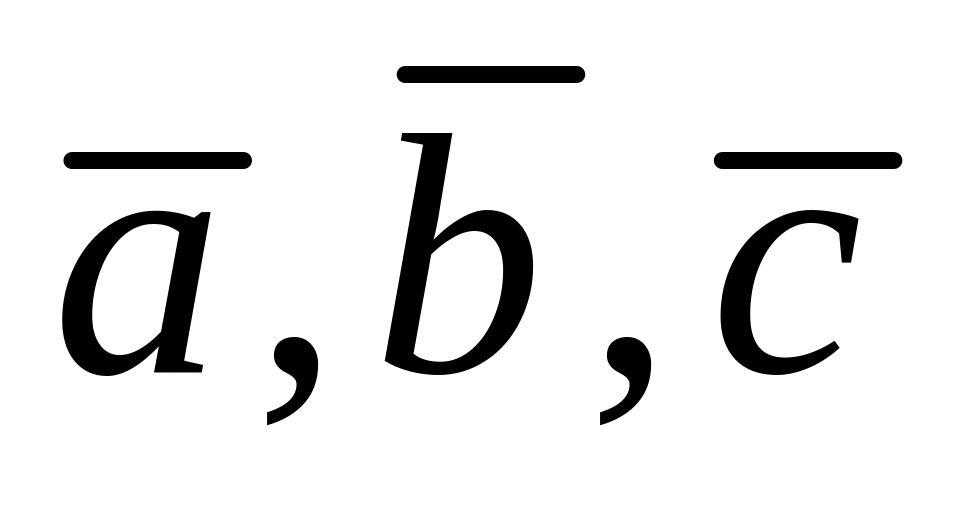 образуют правую тройку
образуют правую тройку
Три не комплонарных вектора a,b,c образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора a ко второму b виден совершающийся против часовой стрелки.
Свойства.
Выражение векторного произведения через координаты.
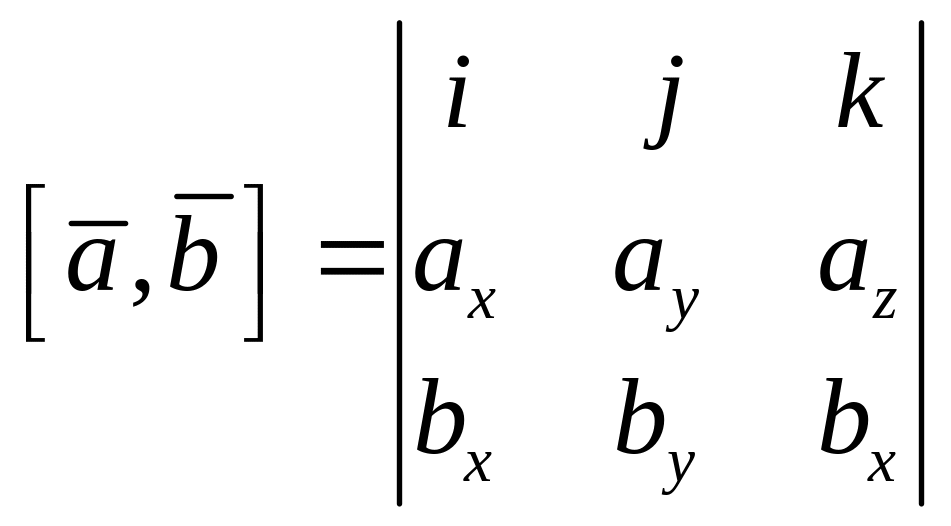
Приложение.
Установление кампланарности векторов.
Если
![]() ,
то
,
то
![]()
![]()
Нахождение площади параллелограмма и треугольника.

16. Смешанное произведение векторов и их свойства.
Смешанное
произведение векторов
![]() и
называются
и
называются
![]()
Свойства.
смешанные произведения не меняются при циклической перестановки со множителями.
![]()
смешанное произведение изменяют знак при перемене мест любых двух векторов со множителями
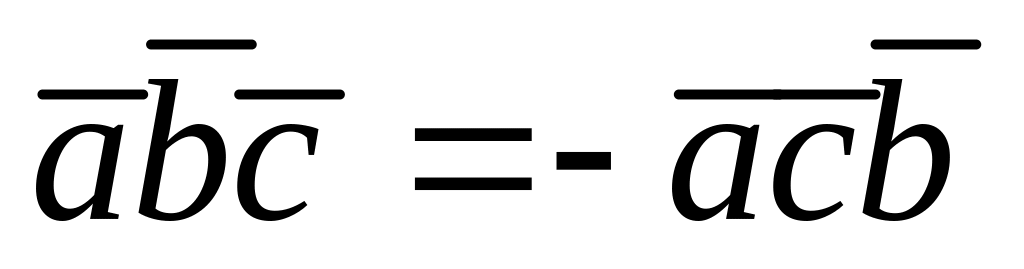
Смешанные произведения равны нулю тогда и только тогда когда a,b,c – комплонарны.
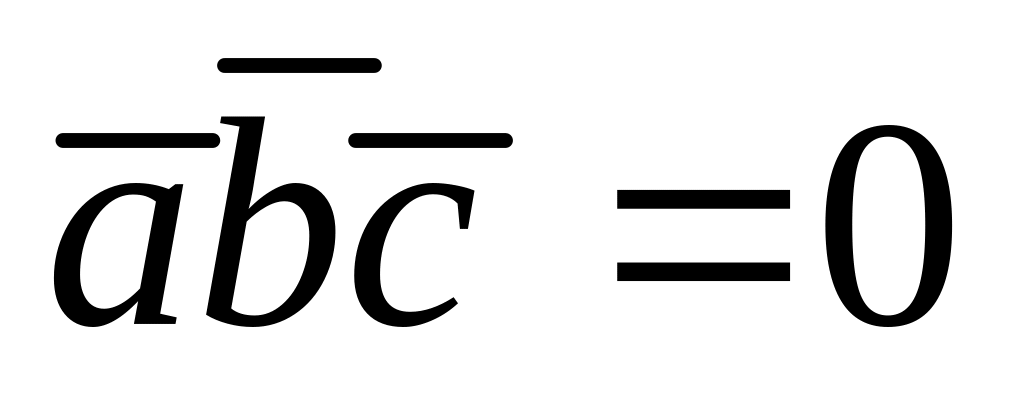
Выражение смешанных произведений через координаты.
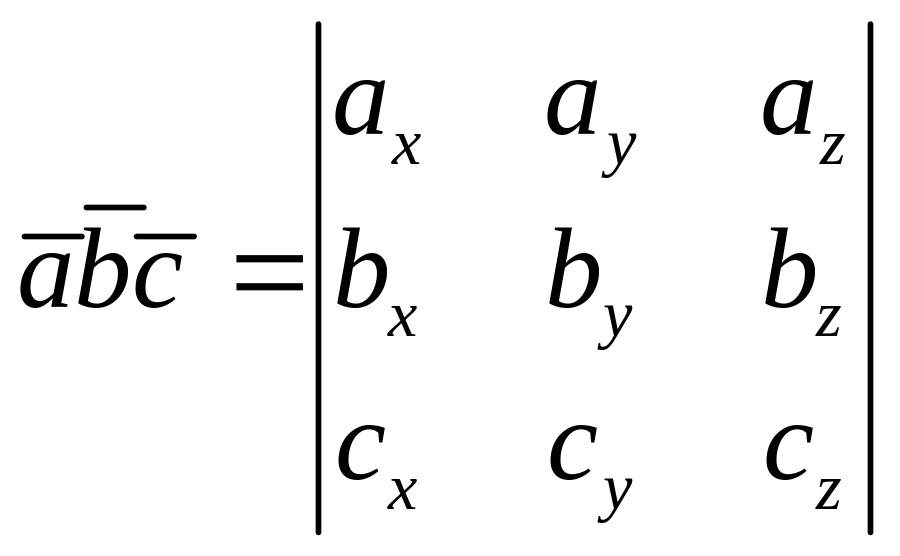
Приложения.
Определение взаимного расположения в пространстве.
![]() -
правая
тройка.
-
правая
тройка.
![]() -
левая
тройка
-
левая
тройка
Объём параллелепипеда и тетраэдра.

