9.Метод крамера.

1.Вычесляем определитель (если =0, то метод не работает)

2.Вычесляем определяемый определитель

3. Вычисляем корни уравнения

10. Решение произвольной слау.

В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n:

Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.

Далее нам потребуется понятие минора матрицы и ранга матрицы, которые даны в статье ранг матрицы: определение, методы нахождения, примеры, решения.

Теорема Кронекера – капели

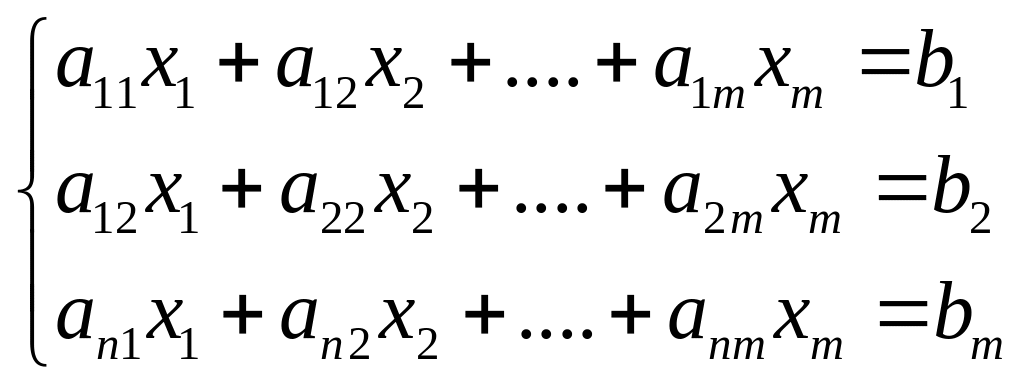
m- неизвестных

n- уравнений

Система (1) называется не совместной если не имеет решений. Совместная система называется определенной если имеет единое решение. Совместна система называется не определенной если имеется множество решений

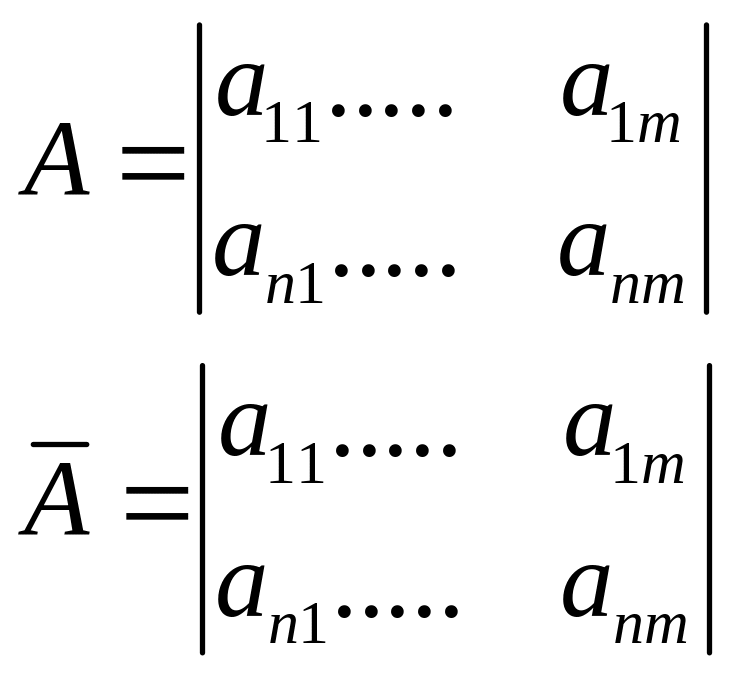
Теорема. Для того чтобы система (1) была совместна, необходимо и достаточно ранг основной матрицы совпадал с рангом расширенной.

11. Метод Гаусса для решения слау. Однородная слау.

Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:

во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;

во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;

в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Однородная слау.

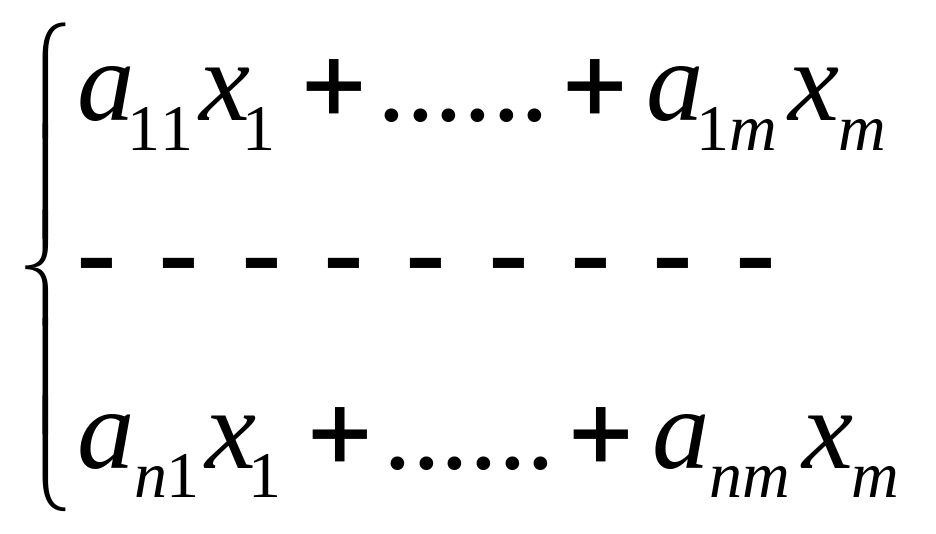
Однородная система всегда совместна.

- тривиальное решение.

Частные случаи : n=m

Свойства.

Пусть 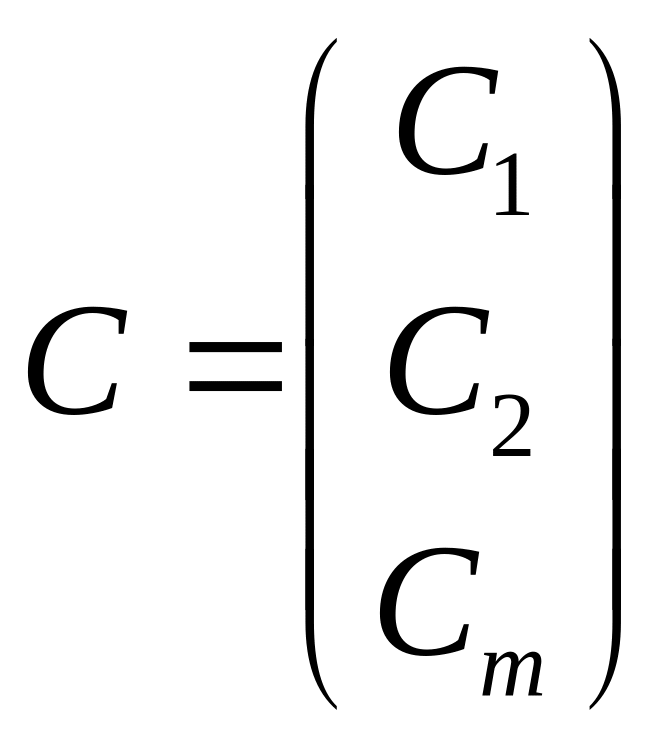и 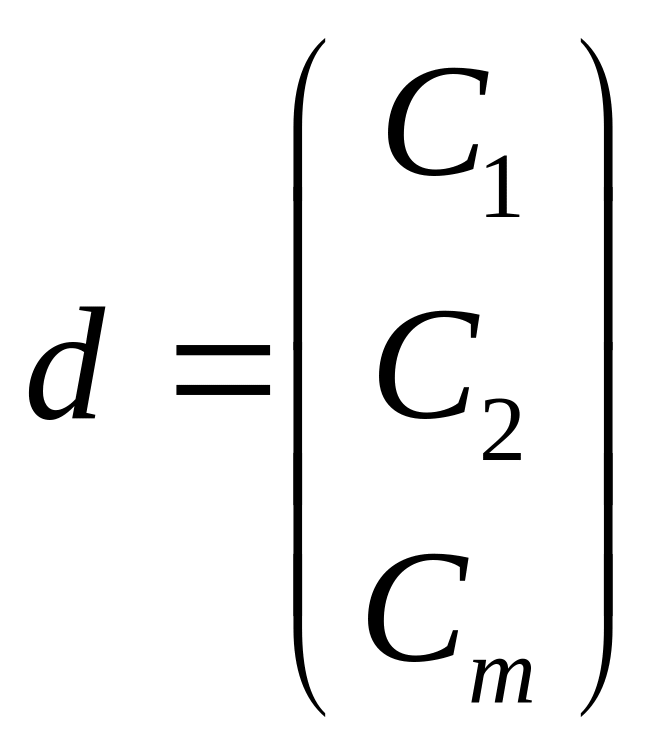- решения

Тогда : C+d; dc – также решение (2)

Пусть 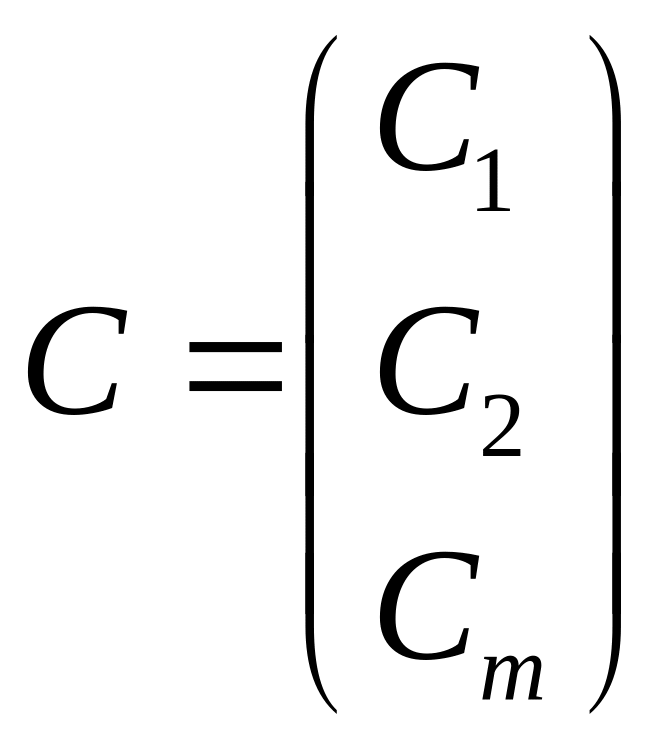- решение (1)

- решение (2)

Тогда C+d – решение (1)

Пусть С – решение (1) и d – решение (1)

Тогда C-d = решение 2

Вывод: общее решение неоднородных уравнений складывается из общего решения однородной системы и любого частного решения неоднородной.

12. Элементы векторной алгебры.

Вектором называется направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если А – начало вектора и В – его конец, то вектор обозначается символом . Вектор можно обозначать и одной малой латинской буквой с чертой над ней, например,. Изображается вектор отрезком со стрелкой на конце. Начало вектора называют точкой его приложения. Если точка А является началом вектора, то мы будем говорить, что вектор приложен в точке А.

Длина (или модуль) вектора   определяется формулой   и обозначается   или 

Вектор , для которого || = 1, называется единичным. Обозначается.

Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора.

Вектор, длина которого равна 0, называется нулевым. Нулевой вектор не имеет определенного направления, а начало и конец его совпадают. Обозначается . Векторыи, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Они могут быть одинаково или противоположно направлены.

Два векторы иназываются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными. Вектор, противоположный вектору , обозначается –. Для векторапротивоположным будет вектор.

Линейные операции над векторами. Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число

.Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону. 

Любая точка пространства с координатами (x, y, z) может быть задана своим радиус-вектором

Координаты (x, y, z) это проекции вектора   на оси координат.