17.Система координат.

Под системой координат понимают способ позволяющий численно описать положение точки в плоскости.

Декартовая система координат.

Координаты точки называется координаты её радиуса вектора. Расстояние между 2-мя точками.

Площадь треугольника с вершинами.

Деление отрезка в заданном соотношении. Требуется отрезок АВ (где А , В в заданном соотношении , тоесть , где М точка на отрезке АВ.

,

Координаты середины отрезка.

,

Полярная система координат.

Положение точки на плоскости определяется расстоянием от неё до полюса и углом между данным расстоянием и осью L. Расстояние r (иногда p) называется радиус – вектор.

Связь декартовой и полярной системой координат.

Совместим полюс с началом декартовой системы координат так чтобы ось L совпала с осью OX

,

Линия на плоскости.

Уравнение линии (кривой) на плоскости OXY называется такое уравнение которому удовлетворяют все точки лежащие на ней.

Способы задания линии (функции):

1. Явный вид 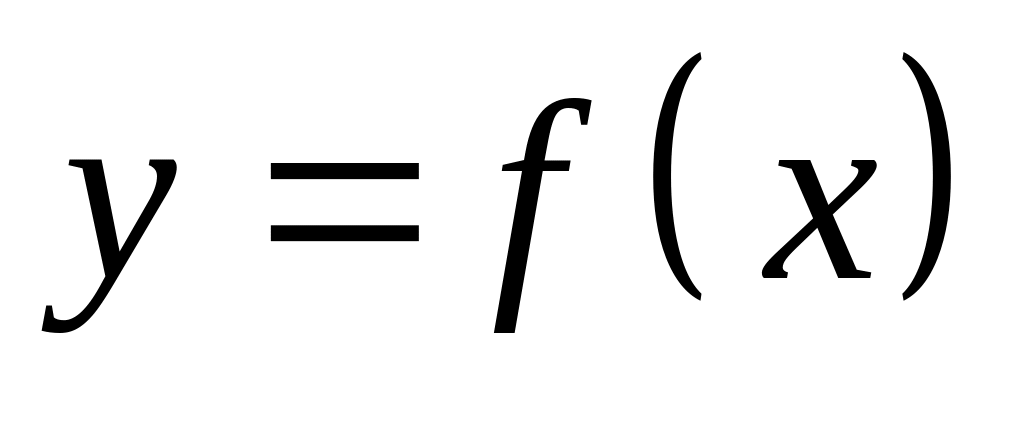, т.е. уравнение разрешено относительно у

2. Неявный вид

Параметрическое уравнение тоесть X и Y представляют собой некоторые функции от параметра (t)

, ,

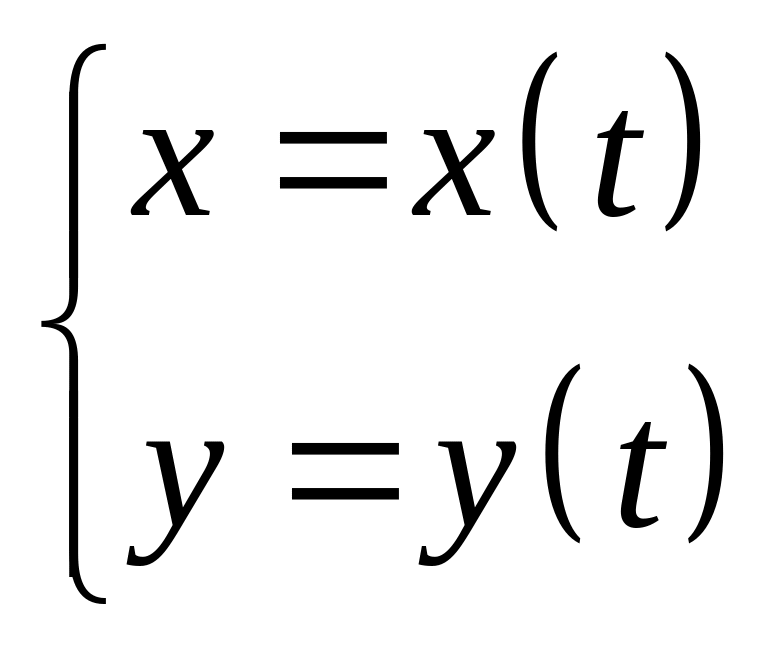Уравнение заданное в полярных координатах

Для того чтобы определить точки пересечения двух линий требуется решить:

18.Уравнение прямой на плоскости.

1.Общее уравнение прямой.

, где А,В,С – числа.

Частные случаи:

- прямая параллельна OX.

- прямая параллельна OY

прямая проходит через начало системы координат

2.Уравнение прямой проходящая через заданную точку перпендикулярное вектору . Выберем некоторую точку М(x,y). Тогда параллельна их скалярное произведение равно нулю.

3.Уравнение прямой проходящие через две заданные точки.

/

4.Уравнение прямой проходящее через заданную точку и параллельной вектору - направляющий вектор.

5.Уравнение прямой с угловым коэфициэнтом . Если

- угловой коэфициэнт.

Условия параллельности и перпендикулярности прямых.

- угол наклона

Угол между двумя прямыми.

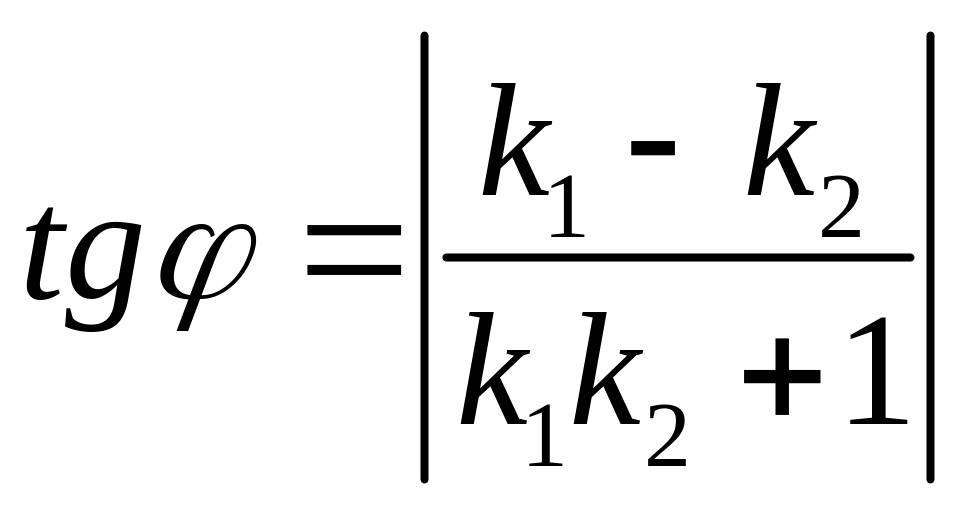
6.Уравнение прямой в отрезке. Прямая отсекает от координатных осей отрезки равная а ( по оси Ox) и b (по оси Oy)

7. Нормальное уравнение прямой имеет вид:

Величины и называются направляющими косинусы .

Переход от общего к нормальному. Умножим уравнение на коэфициэнт и сопоставим полученное уравнение с нормальным.

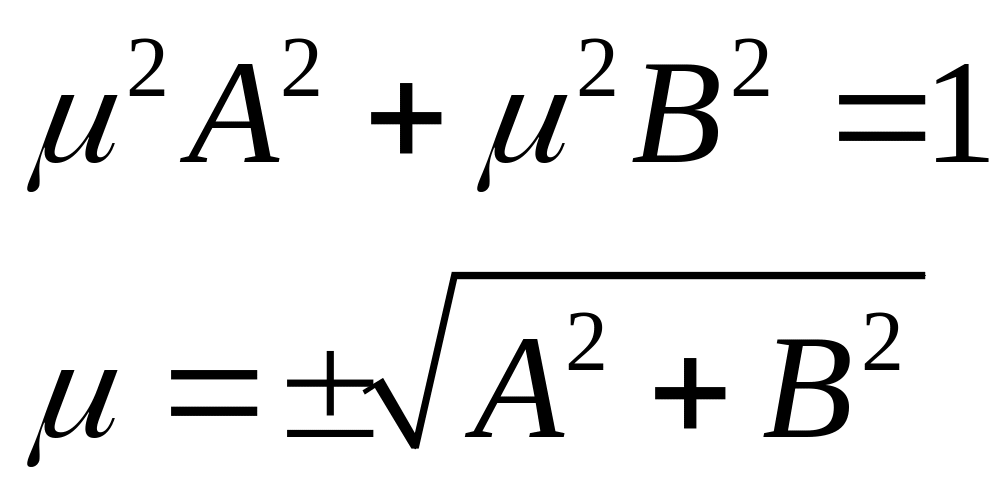, - знак коф. противоложен знаку коф. С

8. Расстояние от точки до прямой. Расстояние от точки до определяется по формуле

4. Матрицы. Основные понятия. Действия над ними.

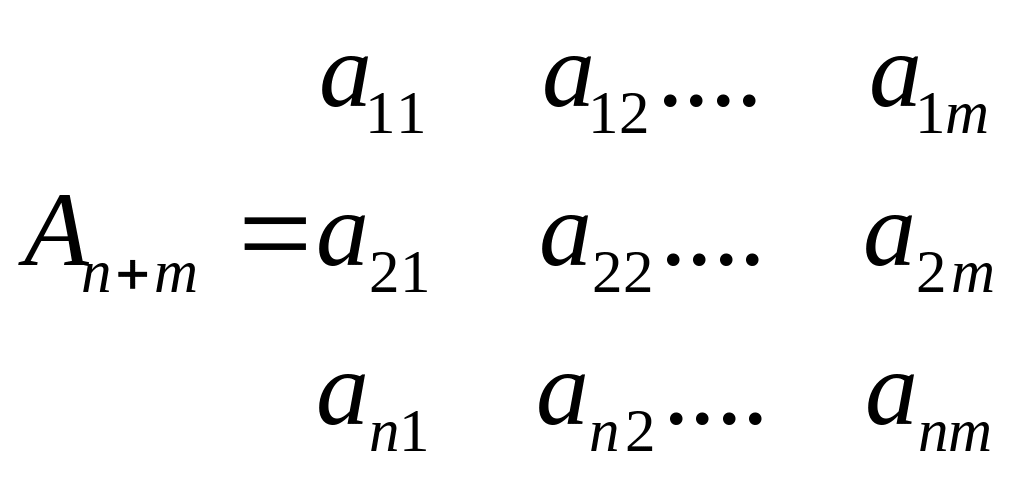Если n=m, то матрица квадратная.

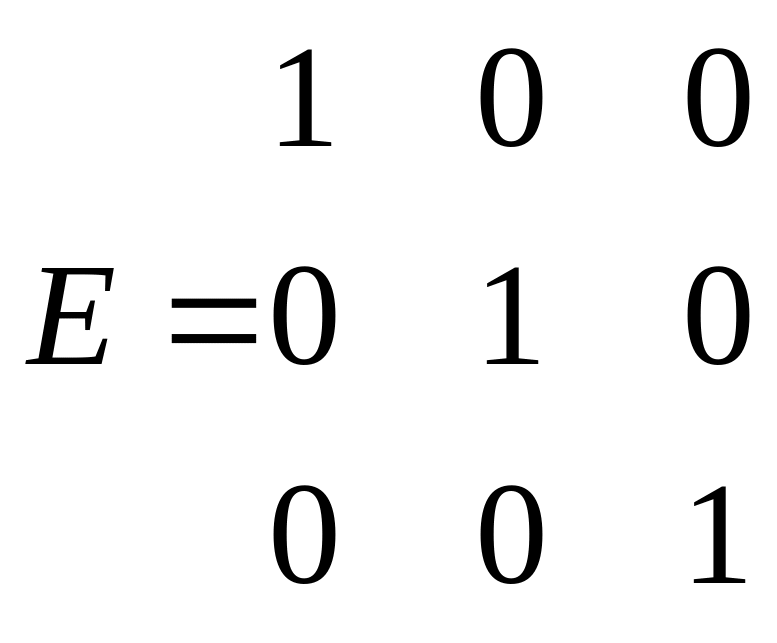- Единичная матрица

Сложение

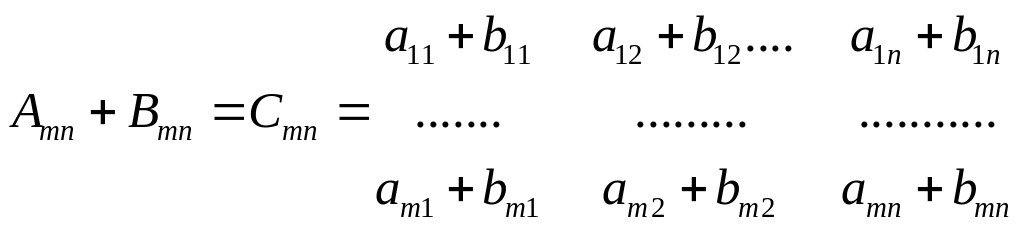
Умножение на число.

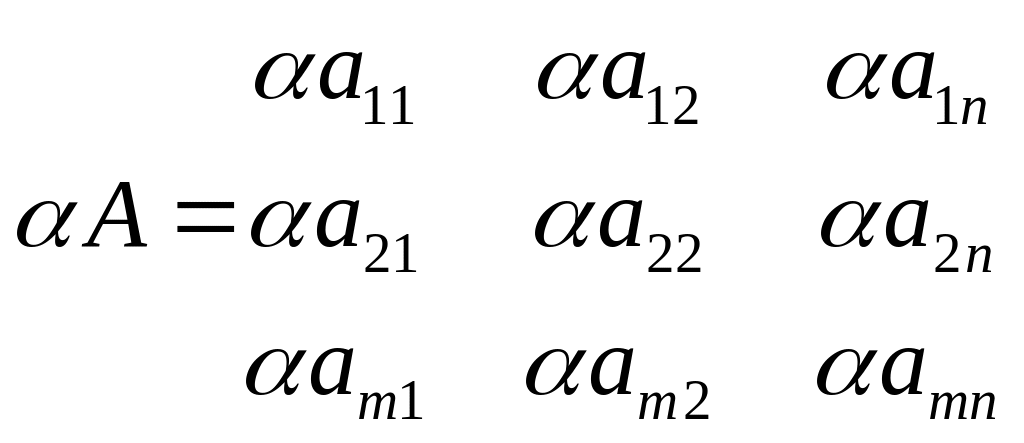
Умножение матриц матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матриц В)

5. Определитель. Основные понятия. Свойства определителя.

Пусть А – квадратная матрица. Тогда или - определитель.

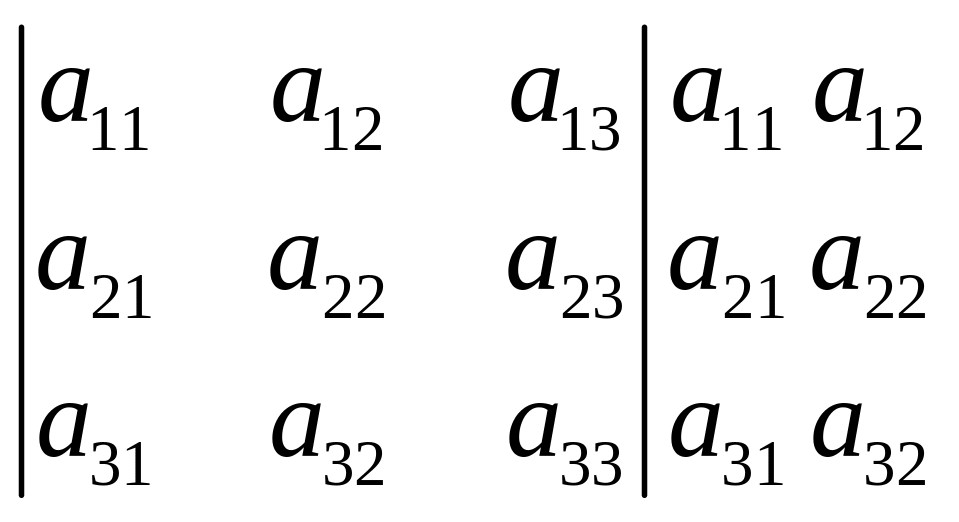
Свойства.

1.

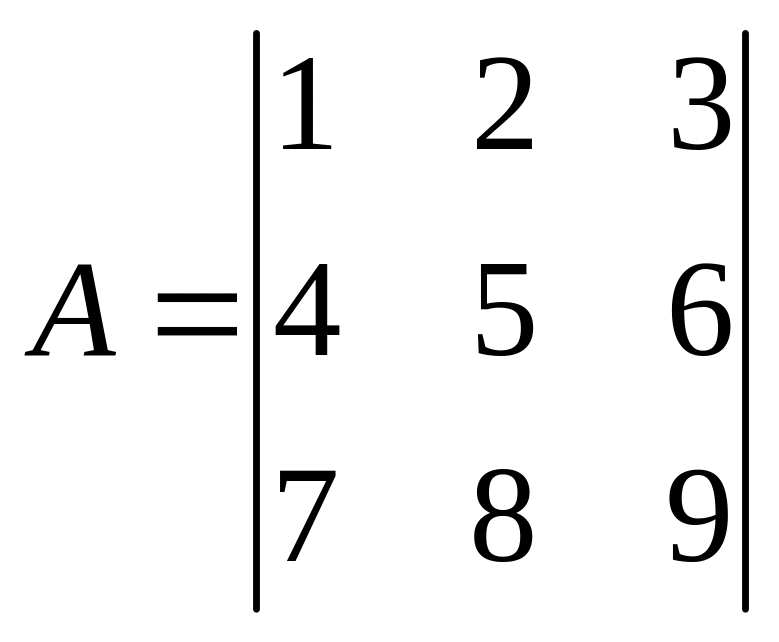
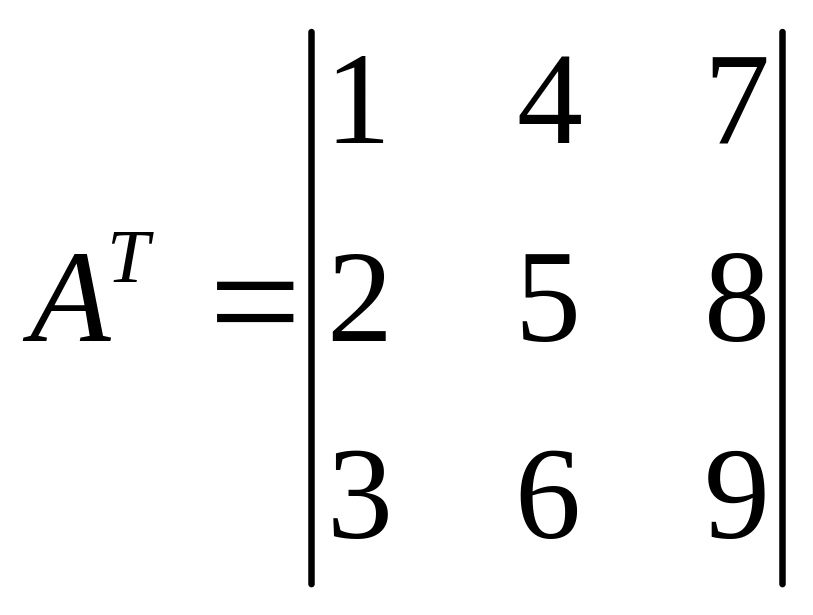
2. Определитель содержащий нулевую строку или столбец равен нулю.

3. Определитель поменяет знак если поменять местами две строки.

4. Общий множитель элементов любой строки можно вынести за знак определителя.

5. определитель не изменится если к элементам одной строки добавить элемент другой строки умноженный на произвольное число.

Минора.

Минора – определитель полученный из исходного вычеркиванием строки с номером и столбца с номером.

6.элементарные преобразования матриц. Ранг. Обратная матрица.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

перестановку местами любых двух строк матрицы;

умножение на ненулевую константу любой строки матрицы;

прибавление к любой строке матрицы другой строки, умноженной на ненулевое число.

Аналогично определяются элементарные преобразования столбцов.

Определение.

 Матрицы A и B называют эквивалентными матрицами если от матрицы A к матрице B перешли с помощью элементарных преобразований над строками и обозначают A ~ B.