96

15 Подкрановые конструкции

15.1 Общие сведения

Подкрановые конструкции (рисунок 15.1) состоят из подкрановых балок или ферм 1, воспринимающих вертикальные нагрузки от кранов, тормозных балок (ферм) 2, воспринимающих поперечные горизонтальные воздействия, узлов крепления, передающие воздействия на колонны, крановых рельсов 3 и связей 4.

	а – схема нагрузок от мостового крана; б – состав подкрановых конструкций по среднему ряду
Рисунок 15.1 – Схема подкрановых конструкций

Основные несущие элементы – подкрановые балки (фермы), имеющие различные конструктивные формы (рисунок 15.2 а, б, в).

Рисунок 15.2 – Типы подкрановых конструкций

Неразрезные балки на 12-15% экономичнее по расходу металла, но более трудоемки.

При легких кранах (Q ≤ 30т) и больших шагах колонн целесообразны решетчатые балки (рисунок 15.2 в).

При больших пролетах (шаг более 24м) и кранах большой грузоподъемности применяют подкраново – подстропильные фермы..

15.1.1 Нагрузки от крана передаются через колеса (катки) крана.

Расчет ведут на нагрузки от двух сближенных кранов с тележками приближенными к одному из рядов колонн. Одновременно к балке прикладываются и максимальные поперечные горизонтальные усилия

F_k=k₁·γ_f·Fⁿ_k; T_k=k·γ_f·Tⁿ_k , (15.1)

где k – коэффициент динамичности (СНиП [4]);

γ_f=1.1;

Fⁿ_k - максимальное усилие на катке (принимают по ГОСТ на краны);

Тⁿ_k определяется по формулам (12.4) или (12.5).

Для кранов особого режима работы учитывается горизонтальная нагрузка, вызываемая перекосом крана, поэтому Тⁿ_k=0.1· Fⁿ_k.

При расчете на выносливость принимаются наиболее часто повторяющиеся нагрузки, которые определяют умножением Fⁿ_k на понижающий коэффициент (0.5 при кранах режима работы 4К-6К; 6-7К; 7-8К).

Проверку жесткости подкрановых балок выполняют на нагрузку от одного крана с γ_f=1,0 и без учета коэффициента «k».

Влияние собственного веса балки допускается учитывать умножением расчетных усилий от вертикальной нагрузки кранов на коэффициент α, равный для балок пролетом 6 м – 1,03; 12 м – 1,05; 18 м – 1,08.

15.2 Сплошные подкрановые балки

15.2.1. Конструктивные решения.

Типы сечений зависят от нагрузки, пролета и режима рабты крана, приведены на рисунке 15.3.

	а – прокатные двутавры; б – несимметричный составной двутавр; в – симметричный составной двутавр с тормозной конструкцией; г – составное сечение с поясами из тавров; д – двутавр с усиленным верхним поясом; е – двустенчатое сечение; ж – клепаное сечение
Рисунок 15.3 – Типы сечений сплошных подкрановых балок

При больших пролетах балок и для кранов Q=50т и более устанавливают тормозные балки или фермы (рисунок 15.4). Обычно применяют балки со стенкой из рифленого листа t=6-8 мм (рисунок 15.4 а), который приваривается к поясам сплошным швом с подваркой с нижней стороны, кроме того снизу укрепляют ребрами жесткости сечением не менее 65х5 с шагом 1,5-2 м.

	а, б, в – по крайним рядам; г, д – по средним рядам; 1 – листовой шарнир; 2 – ребро жесткости; 3 – вспомогательная ферма; 4 – связевая ферма
Рисунок 15.4 – Тормозные балки

15.2.2 Расчет подкрановых балок во многом аналогичен расчету составных балок, но имеет особенности.

Так как нагрузка подвижная, то нужно найти такое ее положение, при котором расчетные усилия будут наибольшими.

Наибольший М_max в разрезной балке возникает тогда, когда равнодействующая всех сил, находящаяся на балке, и ближайшая к ней сила равноудалены от середины пролета (рисунок 15.5 а), при этом М_max будет под силой, ближайшей к середине пролета (правило Винклера).

	а – наибольший изгибающий момент; б – наибольшая поперечная сила
Рисунок 15.5 – К определению расчетных усилий в разрезных подкрановых балках

Наибольшая Q_max будет, когда одна из сил находится непосредственно у опоры, а остальные распложены как можно ближе к этой опоре (рисунок 15.5 б).

Расчетные значения М и Q от вертикальной нагрузки определяют по формулам

M_max=α·ψ·ΣF_ki·y^M_i и Q_x=α·ψ·ΣF_ki·y^Q_i (15.2)

где ψ – коэффициент сочетаний; у_i – ординаты линии влияния М и Q,

α – коэффициент, учитывающий вес балки.

Расчетные значения М_у и Q_у от горизонтальной поперечной нагрузки находят при том же положении кранов:

M_y=ψ·ΣT_k·y^M_i и Q_y=ψ·ΣT_k·y^Q_i (15.3)

Проверка прочности.

Под действием вертикальных и горизонтальных нагрузок подкрановая балка и тормозная конструкция работают как единый тонкостенный стержень на косой изгиб с кручением (рисунок 77) и нормальные напряжения определяют по формуле

σ= , (15.4)

где М_х, М_у – изгибающие моменты относительно главных осей Х₀-Х₀ и У₀-У₀;

В – бимомент;

J_x, J_y – моменты инерции относительно главных осей;

J_w – секторальный момент инерции;

х₀, у₀, ω – линейные и секторальные координаты точки сечения.

	а – сечение балки и эпюра нормальных напряжений в тонкостенном стержне; б – эпюра напряжений в условной расчетной схеме
Рисунок 15.6 – К расчету подкрановых балок

Условно принимается, что вертикальная нагрузка воспринимается только сечением подкрановой балки, а горизонтальная – только тормозной балкой, в состав которой входит верхний пояс подкрановой балки. Тогда. верхний пояс балки работает как на вертикальную, так и на горизонтальную нагрузки и максимальное напряжение в точке А (рисунок 15.6 б) можно определить по формуле

σ_a = M_x/W^A_x+M_y/W^A_y ≤ R_y·γ_c (15.5)

соответственно в нижнем поясе

σ=М_х/W_х^н.п≤R_yγ_c . (15.6)

Устойчивость верхнего пояса из плоскости балки проверяют по формуле

σ= M_x/W^A_x + N_x/φ·A_f+M_loc,y/W^A_y≤R_y·γ_c (15.7)

Значение коэффициента φ определяется по гибкости верхнего пояса относительно вертикальной оси балки при расчетной длине пояса, равной d.

Касательные напряжения в стенке балки определяют так же, как и в обычных балках.

Сосредоточенная нагрузка от колеса крана распределяется на участок стенки _ef вызывая местные нормальные напряжения (рисунок 78), проверка прочности стенки на их действие производится по формуле

σ_loc,y=γ_f1·F_k/t_w·_ef≤R_y·γ_c, (15.8)

где γ_f1 – коэффициент увеличения нагрузки на колесе, принимается равным:

1.6 – при кранах режима 8К с жестким подвесом;

1.4 – 8К с гибким подвесом; 1.3 – при 7К; 1.1 – при прочих кранах.

_ef=ψ· , (15.9)

где ψ=3,25 – для сварных балок;

ψ=3,75 – для клепаных – учитывает степень податливости сопряжения пояса и стенки;

J_1f – сумма собственных моментов инерции пояса и рельса.

	а – в сварной балке; б – в клепаной балке
Рисунок 15.7 – Местные напряжения в стенке подкрановых балок под колесом крана

Стенка балки проверяется также на совместное действие σ, τ и σ_loc на уровне поясных швов:

≤ β·R_y, (15.10)

где β=1.15 – при расчете разрезных балок и 1.3 – при расчете сечений на опорах.

Внецентренность рельса на балке, а также горизонтальная сила Т_к (рисунок 15.8) приводят к возникновению местного крутящего момента, приложенного к верхнему поясу балки и вызывает дополнительные напряжения от изгиба в стенке

σ_fy=2·M_t·t_w/J_f , (15.11)

где J_f = J_t + b_f∙t_f³ / 3 – сумма собственных моментов инерции кручения рельса и пояса.

Рисунок 15.8 – Схема действия вертикальной и горизонтальной сил на подкрановую балку

Моменты инерции кручения рельсов равны, см⁴:

КР50-78; КР70-253; КР80-387; КР100-765; КР120-1310.

Крутящий момент вычисляется по формуле

M_t=γ_f·γ_f1·Fⁿ_k·e+0,75·Tⁿ_k·γ_f·h_r , (15.12)

где e=15 мм; h_r – высота рельса.

Помимо вышеуказанных напряжений в стенке балки возникают дополнительные компоненты напряженного состояния: напряжения от распорного воздействия F_к; местные касательные напряжения от F_к; местные касательные напряжения от изгиба стенки.

При проверке прочности стенок балок под краны особого режима следует учитывать все компоненты напряженного состояния.

Расчет на выносливость выполняют при числе циклов n ≥10⁵. В разрезных балках при ρ≥0 усталостная прочность, как правило обеспечена. В неразрезных – при ρ<0, проверка эта может оказаться решающей, что потребует увеличения сечения.

σ_x≤α·R_v·γ_v, (15.13)

где σ_х= М_х/W_х;

R_v – расчетное сопротивление усталости;

α – зависит от числа уголков;

R_v, α и γ_v – определяют по СНиП.

Проверка прогиба производится от одного крана без учета коэффициента динамичности

f=M^н_x·²/10EJ_x . (15.14)

В неразрезных балках

f= , (15.15)

М_л; М_ср; М_пр – соответственно, моменты на левой, в середине, правой опоре.

Предельно допустимый прогиб балок установлен в зависимости от режима работы кранов: 1К – 6К [f]=(1/400); 7K – (1/500); 8K – (1/600). Горизонтальный прогиб не должен превышать (1/2000).

Местная устойчивость элементов проверяется как и у обычных балок.

Устойчивость стенки проверяется по формуле

≤ γ_c=1,0 (15.16)

Ребра жесткости шириной не менее 90 мм, не привариваются к поясам, торцы плотно пригнаны, а под краны особого режима работы – необходимо строгать.

Соединения поясов со стенкой кроме сдвигающих усилий воспринимают сосредоточенное усилие от колеса крана F_к, поэтому проверка производится по результирующему напряжению

τ_w= ≤R_wf·γ_wf·γ_c , (15.17)

где τ_w1=Q∙S_f/(2J_x∙β_f∙k_f);

τ_w2=γ_f1∙F_к/(2_ef∙β_f∙k_f).

Аналогично определяются напряжения по границе сплавления. Тогда, требуемая высота шва будет равна

k_f ≥ 1/2(β·γ_w·R_w)_min·γ_c·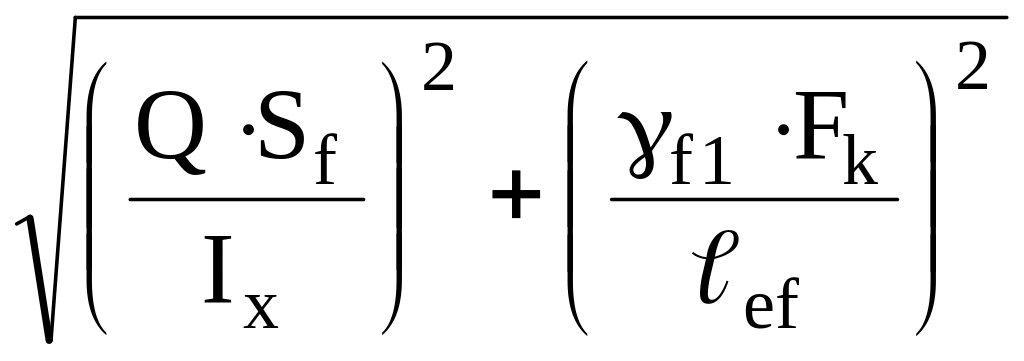 . (15.18)

Нижние поясные швы рассчитывают только на τ.

В клепаных балках шаг заклепок определяется по формуле

a ≤ N_min/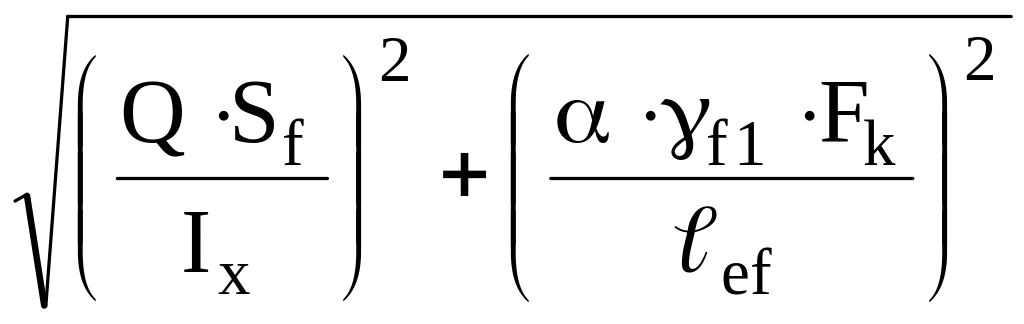 , (15.19)

где N_min – наименьшее расчетное усилие на одну заклепку;

α=0,4 – если стенка пристрогана к обушкам поясных уголков;

α=1,0 – если пристрожки нет.

15.2.3 Подбор сечения балок выполняют в том же порядке, что и обычных балок. Влияние горизонтальных поперечных нагрузок учитывается коэффициентом β. Тогда, из условия общей прочности

σ_x = M_x·β/W_x ≤ R_y·γ_c (15.20)

где

β = 1+M_y·W_x/M_x·W_y = 1+2·M_y·h_b/M_x·h_T (15.21)

Ширину тормозной конструкции принимают h_т=h_н, а высоту балки задают в пределах h_b=(1/6-1/10).

Вычисляют

W_тр=M_x·β/R_y·γ_c, (15.22)

Из условия полного использования материала определяют

h_min=S·γ_c·R_y·/(24βE)[/f]·Mⁿ_x/M_x (15.23)

Определив требуемую площадь поясов, назначают их размеры из условий местной устойчивости при упругой работе b_ef/t_ef ≤ 0,5∙ и возможности размещения рельса с креплениями.