Лекція 11. Формування початкових уявлень про дроби в початковому курсі математики

Витяг з програми

3 клас

Зміст навчального матеріалу

Державні вимоги до рівня загальноосвітньої підготовки учня

Частини Дроби з чисельником 1 як частина цілого. Утворення і запис. Поняття про дріб, чисельник і знаменник дробу. Риска дробу як знак ділення. Порівняння дробів із чисельником 1. Знаходження частини від числа. Знаходження числа за його частиною

Учень (учениця): розуміє утворення частин способом ділення цілого на рівні частини й виділенням однієї з них; визначає кількість певних частин у цілому; визначає, у скільки разів певна частина менша за ціле та у скільки разів ціле більше за частину; читає і записує частини у вигляді дробу з чисельником 1; розуміє сутність чисельника і знаменника дробу, пояснює їх на прикладах; порівнює дроби з чисельником 1 за допомогою засобів наочності; застосовує в обчисленнях правило знаходження частини від числа та числа за його частиною

4 клас

Зміст навчального матеріалу	Державні вимоги до рівня загальноосвітньої підготовки учня
Дроби Поняття «дріб». Читання та запис дробів. Чисельник і знаменник дробу. Дроби, які дорівнюють одиниці. Порівняння дробів. Рівні дроби. Знаходження дробу від числа. Знаходження числа за значенням його дробу.	розуміє спосіб одержання дробу; розуміє значення чисельника і знаменника дробу; читає і записує дроби; розрізняє дроби, які дорівнюють 1; порівнює дроби з однаковими знаменниками; застосовує правила знаходження дробу від числа та числа за значенням його дробу під час розв’язування практично зорієнтованих завдань

1. Ознайомлення з частинами

Перше знайомство з поняттям частини цілого та частини числа відбувається ще при вивченні таблиць множення і ділення (ділення числа на 4). Перед цим на попередніх уроках розглядались вправи, через які вводилось поняття ділення на рівні частини.

Перед тим, як вводити поняття частини, вчитель повинен провести бесіду, щоб впорядкувати і систематизувати життєвий досвід дітей про частини цілого:

• що означає «половинка хліба»? (Цілу хлібину розрізали на дві рівні частини і взяли одну з них).

• Як перевірити, що половинки рівні? (Накладанням).

• Що одержимо, коли дві половинки хлібини складемо разом? (Цілу хлібину).

• Можна розглянути ще кілька подібних прикладів(яблуко, геометричні фігури)

Висновок: Половина – це одна з двох рівних частин цілого.

Практична робота

Кожен з учнів має перед собою смужку паперу, довжиною 8см, аркуш прямокутної форми, круг.

Завдання дітям:

• Склади аркуш паперу навпіл; покажи половинку цього аркуша; що можна сказати про половинки?

• Аналогічна робота з кругом;

• Як поділити смужку навпіл? (скласти її).

• Поміряйте довжину половини смужки (4см).

• Як знайти довжину половини смужки, не згинаючи її? (довжину смужки поділити на 2).

Ознайомлення з поняттями «третя частина», «четверта частина» проводиться також з опорою на наочність, поданою у підручнику:

• Третя частина

  На скільки рівних частин поділена смужка? ( на 3);

• Як називається одна така частинка? (Третя частина);

• Ми можемо назвати її ще одним словом - третина;

• Яка довжина всієї смужки? (12см);

• Як знайти довжину третини смужки? (довжину всієї смужки ділимо на 3);

• То яка довжина третини смужки? (12 см : 3 = 4 см);

За подібною схемою вводиться поняття «четверта частина» (чверть).

Для більш глибокого засвоєння понять «половина», «третина», «чверть» лабораторно-практичним методом можна провести ще і роботу з використанням кругів: розрізати круг на частини, показати накладанням, що всі вони рівні, показати половину, третину, чверть круга, порівняти їх (висновок: чим на більшу кількість частинок ділимо, тим менша величина кожної такої частинки); вияснити, що круг (ціле) складається з двох половинок, трьох третин, чотирьох четвертин.

Після дій з наочністю можна вже опрацювати завдання, подане словесно:

1. Знайдіть четверту частину числа 20 (Щоб знайти четверту частину числа, треба число поділити на 4. 20 : 4 = 5. Четверта частина числа 20 становить 5).

2. Знайдіть п’яту частину від 1дм (Щоб знайти п’яту частину цілого, потрібно його поділити на 5. 1дм на 5 не ділиться. Тому 1дм перетворюємо в сантиметри. 1дм = 10см. 10см : 5 = 2см. П’ята частина 1дм становить 2см).

Позначати частини за допомогою цифр навчають також з використанням відповідного наочного матеріалу:

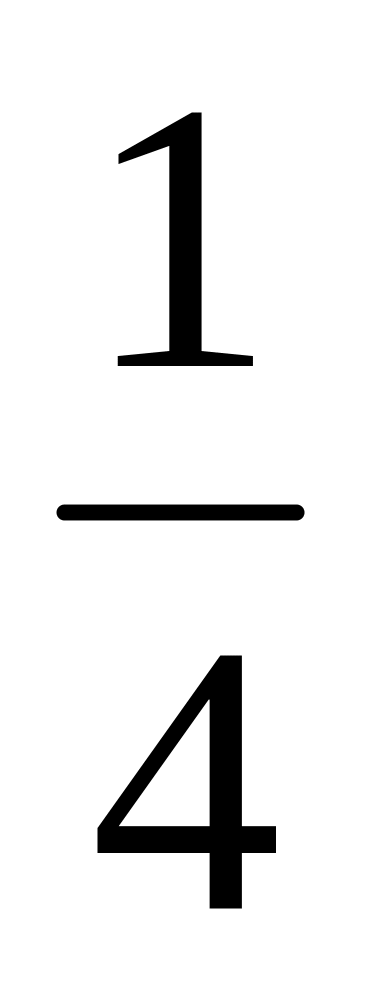• Для позначення половини цілого використовуємо дві цифри 1 і 2, записані одна під одною і розділені рискою: (риска пишеться на лінії клітинки). Число 2 під рискою показує, що ціле розділили на дві рівні частини, число 1 над рискою показує, що взяли одну таку частинку. Читається «одна друга». Аналогічно вводяться записи , і т.п. Порівняння частин з використанням наочності. М.4. , впр. 649, с. 99.

• Використовуючи наочність, можна порівняти частини з чисельником 1: > ; < . Висновок порівняння: чим більше число під рискою (знаменник), тим менше значення частини.