11.2.5. Основні співвідношення між елементами трикутника

Якщо ввести позначення (див. рис. 11.18): а, b, c – сторони трикутника, , , , – кути, протилежні до цих сторін відповідно, – півпериметр, R i r – радіус описаного та вписаного кіл відповідно, , , – висоти, проведені до сторін а, b, c; і – відповідно бісектриса і медіана, проведені до сторони а.

Рис. 11.18

1. (с – найбільша із сторін).

2. (радіан), , , .

3. Теорема синусів .

4. Теорема косинусів .

5. .

6. .

7. .

11.2.6. Формули для обчислення площі трикутників

Простою називається така плоска фігура, яку можна розбити на скінчене число плоских трикутників.

Площею простої фігури є додатна величина, що має такі властивості:

1) за одиницю вимірювання площі приймається площа квадрата із стороною, рівною одиниці;

2) кожна проста фігура при заданій одиниці вимірювання має певну площу;

3) рівні фігури мають рівні площі;

4) якщо фігуру розбито на частини, що є простими фігурами, то площа фігури дорівнює сумі площ цих її частин.

Дві прості фігури, що мають рівні площі, називаються рівновеликими.

Говорячи про площі трикутника, матимемо на увазі площі областей, обмежених ними.

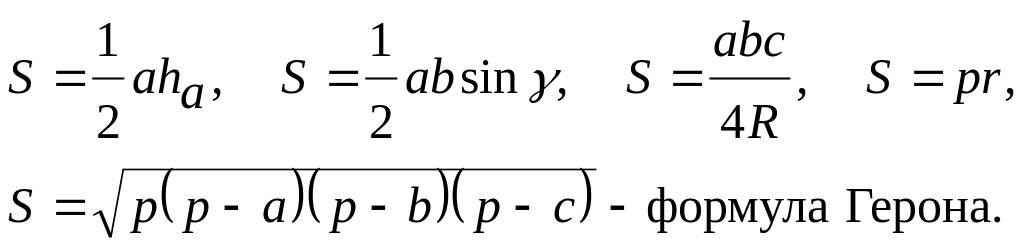
11.2.7. Середня лінія трикутника

Середня лінія трикутника – це відрізок, що сполучає середини двох його сторін. Трикутник має три середніх лінії.

Властивість середньої лінії: середня лінія трикутника паралельна третій стороні і дорівнює її половині.

На мал. 11.19 штрихами позначено рівні сторони: АЕ=ЕВ, BF=FC, CD=DA, де DE, EF, FD – середні лінії трикутника ABC.

Середня лінія DE відтинає від даного трикутника ABC трикутник ADE, подібний трикутнику ABC, площа якого .

Середні лінії трикутника ділять його на чотири однакових частини:

.

Рис. 11.19	Рис. 11.20

11.2.9. Окремі види трикутників та їхні властивості

11.2.9.1. Рівнобедрений трикутник

Дві рівні між собою сторони рівнобедреного трикутника називають бічними сторонами, а третю – основою трикутника. На рис. 11.20 АС, ВС – бічні сторони, АС=ВС, АВ – основа.

Властивість кутів при основі рівнобедреного трикутника: кути при основі рівнобедреного трикутника рівні між собою, наприклад, на рис. 11.20 .

Властивість висоти рівнобедреного трикутника: висота, проведена до основи рівнобедреного трикутника, є одночасно медіаною і бісектрисою цього трикутника:

11.2.9.2. Правильний трикутник

11.2.9.3. Прямокутний трикутник



Приклади

Рис. 11.21

Приклад 11.1. Дано рівнобедрений трикутник . На прямій АВ розміщено точки М і N так, що . Точка В лежить між точками А і М, точка А лежить між точками В і N. Довести, що: а) , б) (рис. 11.21).

 а) Оскільки , то і згідно з першою ознакою рівності трикутників ;

б) , бо кути СВМ та САN суміжні до рівних кутів А і В.

Отже, за першою ознакою. 

Приклад 11.2. Кут між бісектрисою і висотою, які виходять з однієї вершини рівнобедреного трикутника, дорівнює . Знайти кути трикутника.

 Зрозуміло з умови, що висота і бісектриса проведені з вершини при основі рівнобедреного

Рис. 11.22	Рис. 11.23

трикутника. Можливі два випадки.

1) Бісектриса AD проходить між висотою АЕ і

основою АВ (рис. 11.22). Нехай , тоді . З маємо: , звідки . Отже, , а .

2) Бісектриса AD проходить між висотою АЕ і бічною стороною АС (рис. 11.23). Якщо , то . Отже, . З маємо: або , звідки , і . Відповідь: або . 

	Питання для самоперевірки

1. Які геометричні фігури є основними?

2. Що називається променем, відрізком?

3. За яких умов відрізки рівні між собою?

4. Дайте означення кута, бісектриси кута

5. За яких умов кути рівні між собою?

6. Які кути називаються суміжними, вертикальними? Сформулюйте властивості цих кутів.

7. Прокласифікуйте кути в залежності від їхньої градусної міри.

8. Що називається кутом між двома прямими?

9. Які прямі називаються паралельними, перпендикулярними?

10. Перелічіть кути, що утворюються в результаті перетину двох прямих січною. Запишіть властивості цих кутів, за умови, що прямі, які перетинаються січною, паралельні.

11. Дайте означення трикутнику.

12. Які існують трикутники в залежності від довжин сторін та градусних мір кутів?

13. Що називається медіаною, бісектрисою та висотою трикутника? Запишіть властивості перелічених елементів.

14. Запишіть основні співвідношення між елементами трикутників та формули площ, якщо трикутник:

    • різносторонній;

    • рівнобедрений;

    • рівносторонній;

    • прямокутний.

15. Дайте означення та сформулюйте основні властивості таких трикутників:

    • рівнобедрений;

    • рівносторонній;

    • прямокутний.



Вправи

1. У прямокутному трикутнику точка дотику вписаного кола поділяє гіпотенузу на відрізки довжиною 5 і 12 см. Знайти катети трикутника.

2. У рівнобедреному трикутнику з бічної сторони, рівної 4 см, проведена медіана бічної сторони. Знайти основу трикутника, якщо медіана дорівнює 3 см.

3. Кожна сторона правильного трикутника розділена на три рівні частини, і відповідні точки розподілу, вважаючи в одному напрямку, з'єднані між собою. В отриманий правильний трикутник вписане коло радіуса  см. Визначити сторони трикутників.

4. Визначити гострі кути прямокутного трикутника, якщо медіана, проведена до його гіпотенузи, поділяє прямий кут у відношенні 1:2.

5. Знайти довжини сторін АВ і АС трикутника АВС, якщо ВС = 8 см, а довжини висот, проведених на АС і ВС, рівні відповідно 6,4 і 4 см.

6. Медіана, проведена до гіпотенузи прямокутного трикутника, дорівнює т і поділяє прямий кут у відношенні 1:2. Знайти сторони трикутника.

7. У трикутнику довжини двох сторін складають 6 і 3 см знайти довжину третьої сторони, якщо напівсума висот, проведених до даних сторін, дорівнює третій висоті.

8. Точка на гіпотенузі, рівновіддалена від обох катетів, поділяє гіпотенузу на відрізки довжиною 30 і 40 см. Знайти катети трикутника.

107